传统正则化方法和Bayes统计理论之间的联系

陈伟,王子亭

(中国石油大学数学与计算科学学院,山东青岛266555)

0 引 言

所谓反问题是相对正问题而言的,从数学模型的角度上来看,就是针对一个系统就已知和未知的相互转化关系不同而建立起来的俩个相互关系的模型,可以视为是一个问题的俩个方面,就一个系统而言,正与反是相对的,没有绝对的标准。

但是实际问题的处理中,人们总是由易到难,把复杂的问题转化为简单的问题,把未知的问题转化已知的来处理,这样把已经解决或部分解决的问题定型化,建立起相应的数学模型。

随着人们认识水平的提高和解决实际问题的需要,原来模型中已知变成了人们更感兴趣的未知的,而原来未知的通过测量变为已知或部分已知的,这样就出现与原模型相反的问题。人们常把相互关联的一对问题中比较简单已经得到部分解决或部分解决的问题称为正问题,而把另一问题称为反问题。数学推理的严密的逻辑性要求人们提出数学问题建立数学模型,首先考虑问题的合理性,即问题的适定性,简单说来就是要求解存在唯一且稳定。

因此,在实践中人们首先研究的是适定的问题,且认为不适定的问题不是一个好的数学问题,甚至有人认为研究不适定的问题是没有意义的。原来研究比较成熟的问题大多由因求果,满足因果律,属于向前问题,大多属于预测或解释型的,在实践中用的最多的或者更有意义的是认知自然,对系统进行建模,由果推因,这样就提出了不满足因果律的不适定问题。数学因“用”而生,由“用”而长,广泛的应用领域催生了反问题的诞生和发展。虽然正问题和反问题是相对的,但实际上各个应用领域中提出的反问题都是不适定的。人们把不适定作为反问题的一个特征,其核心是稳定性条件不满足。

1 简介求解反问题的正则化方法和Bayes统计方法的思想

反问题求解的经典方法是正则化方法[1],其核心是用一系列适定的近似问题去逼近不适定的反问题。不论是Tikhonov正则化方法,还是迭代正则化方法,它们主要是针对已知数据有误差情况下,如何构造近似算法得到原问题的一个近似解。

反问题的Bayes统计方法把数据视为随机变量[2,3],所要求的模型参数也是一个随机变量,将模型参数的先验分布信息和已知数据的分布信息结合起来,求模型参数的后验分布。

2 传统正则化方法和Bayes统计方法之间的联系

为更直观的分析传统的正则化方法和Bayes统计方法之间的辩证关系,我们以一类比较常见的正则化方法为例,分别给出正则化方法和Bayes统计方法的求解方法。

下面的是我们比较感兴趣的一类热传导反问题[4]

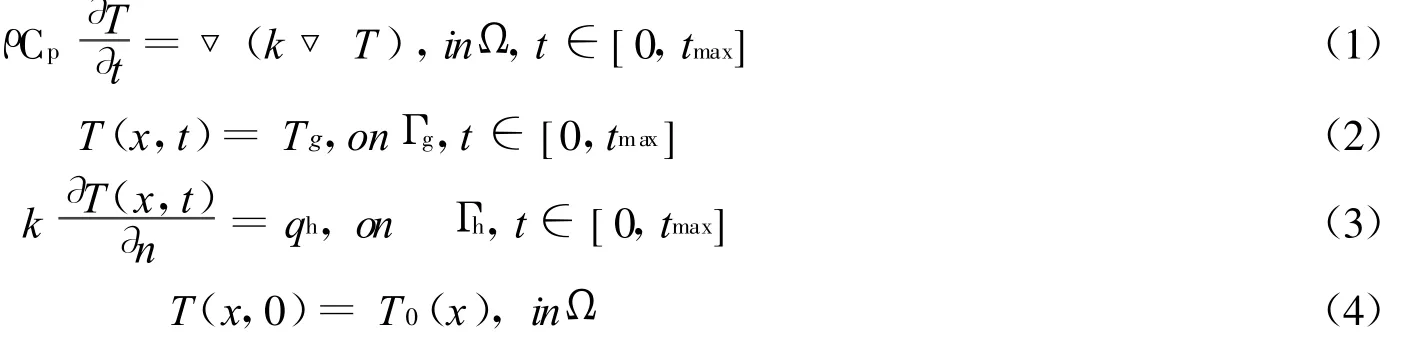
此类反问题的主要计算目标是q0的计算

除了方程(1)～(4)是已知外,我们还可获得区域内部中M个结点的测量值。

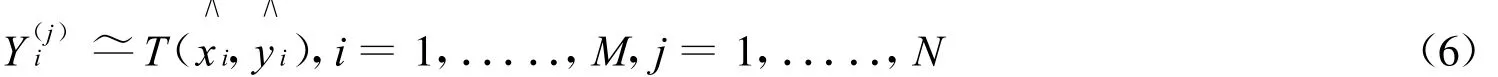
假定q0是已知的,方程(1)～(5)定义了一个适定的正问题,对应正问题的解我们可以记作T(x,t;q0)。对于上述反问题,我们对能够使由正问题求得的匹配好测量数据Y的q0感兴趣。

在求解q0(x,t)之前,我们对其做一下处理,将其用基函数在时间和空间上在有限维空间上线性的近似离散化,表示如下

有了线性离散化之后,我们对q0(x,t)的求解就转化为对θ的求解

我们先介绍下正则化方法对该反问题的处理方法,对于传统的正则化方法求解反问题而言,它考虑的反问题的各个变量是确定的,而不是随机的。用最小二乘的思想来考虑,求解此反问题即是求解向量θ使其满足极小化

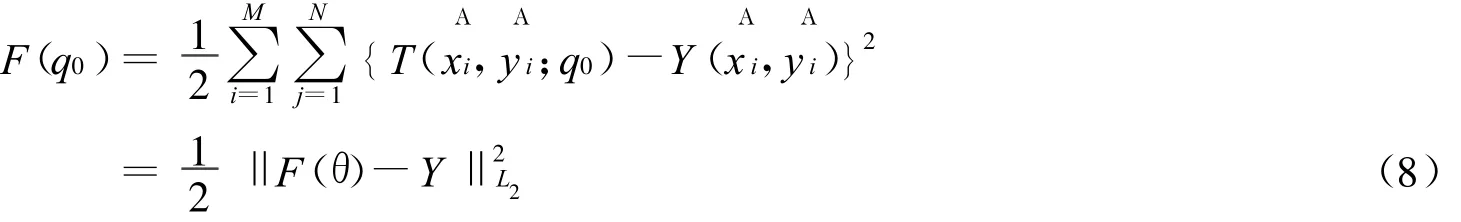
但是由于反问题的不适定性,需要我们加上一些约束性条件,就引入了正则化方法,将上面的最小二乘问题(8)进行改进便得到了Tikhonov正则化方法,将求解θ极小化(8)的问题转化为求解极小化下式

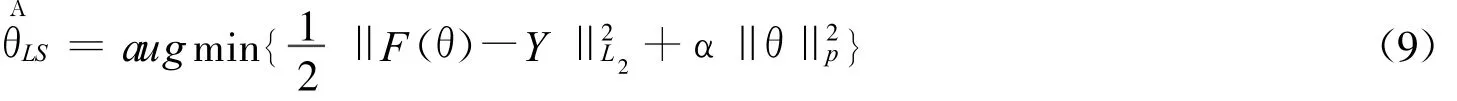
从而求反问题参数的问题转化为一个优化问题,即求能使极小化(9)的θ。

下面介绍下求解反问题的Bayes统计方法。

用Bayes统计方法求解问题,即此时我们考虑反问题中的参数θ是一个随机变量,并且所得到的额外的观测数据也是有误差的,比较符合实际的情况。我们简单的介绍下Bayes统计方法中用的基础知识。

Bayes公式如下

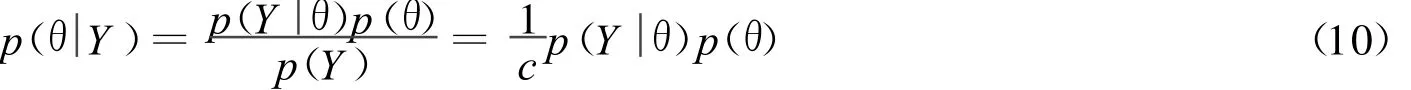
基于后验概率密度我们做的最通常的估计有:取后验概率密度函数的均值

或者取最大后验估计(MAP)

对于θ一定下,Y的分布服从Gauss正态分布,即

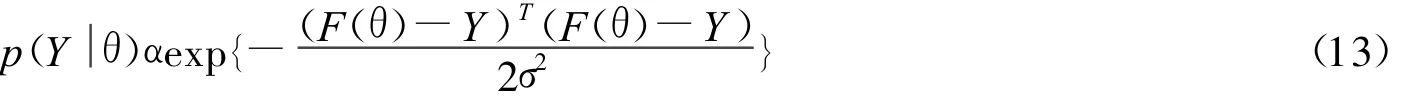
对于先验分布模型,MRF被认为是一个合适的选择,

由Bayes公式,可得θ的后验概率密度函数PDF为

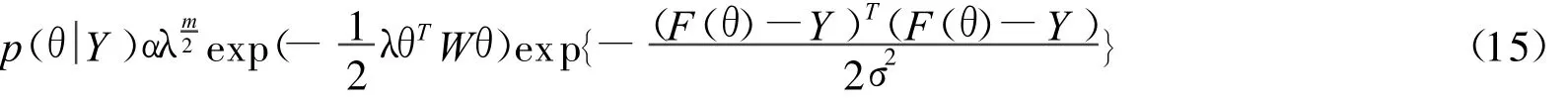
由(15)可得θ的最大后验估计MAP为

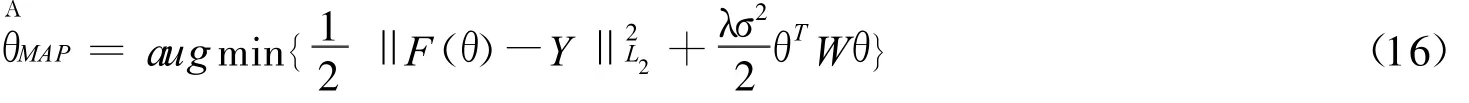
求(16)便得到反问题的一个估计,σ已知的情况下(16)中λ便起着正则化参数的作用,而不同的W对应于参数空间θ的某种范数。故从以上的例子中我们可以看到经典的正则化方法是统计方法的特例,正则化方法得到的解对应于从后验分布中获得的数字特征。

3 结束语

反问题的Bayes方法具有广泛的应用领域,包括地球物理探测以及气象建模和微分方程系统的参数识别反问题,而Bayes方法在应用中的主要计算挑战是从后验分布中提取信息。

一定意义上可以说,经典的正则化方法是统计方法的特例,因为从后验分布可以计算各种形式的数字特征,对应于经典正则化方法的点估计。

[1] 刘继军.不适定问题的正则化方法及应用[M].北京:科学出版社,2005.

[2] JariKaipio,Erk kiSomersalo.Statistical inverse problems:Discretization,model reduction and inverse crim es.[J].Journal of Com putationaland Apllied M athematics,2007(198):493～504.

[3] 李书,卓家寿,任青文.动力参数识别中的Bayes方法.[J].应用数学和力学,2000,21(4):402～408.

[4] Jingbo Wang.Nicholas Zabaras,Johnny Henderson,.A Bayesian inference app roach to the inverse heat conduction problem.[J].International Jou rnal of H eat and Mass T ransfer,2004(47):3927～3941.