电磁波极化实验的改进
2011-03-21贾建科韩团军
贾建科,聂 翔,韩团军
(陕西理工学院 电信工程系,陕西 汉中 723003)
极化在雷达信号滤波、检测、增强、抗干扰、目标鉴别/识别等方面都有着巨大的应用潜力[1]。同时,在进行电磁波的极化实验教学时,可帮助学生对极化概念和三种极化方式的正确理解[2]。在电磁波极化实验中所用的微安表头指示精度低,而实验中接收到的电磁波信号又很弱,用微安表头观测实验现象很不清晰。但利用万用表可以明晰地观测到电磁波的三种极化现象。还可利用Matlab语言对实验数据进行可视化处理,以提高实验教学效果。
1 电磁波极化
电磁波的极化是电磁理论中的一个重要概念,它表征在空间给定点上电场强度矢量E的取向随时间变化的特性,并用电场强度矢量E的端点随时间变化的轨迹来描述[3]。若E轨迹是直线,则称为直线极化;若E轨迹是圆,则称为圆极化;若E轨迹是椭圆,则称为椭圆极化。本文主要讨论电磁波的圆极化和椭圆极化。如沿+z方向传播的均匀平面波,由两个分量组成,它们是两个同频率的线极化波,其电磁场强度的复矢量为

Ex和Ey分别为x分量和y分量的复振幅,即
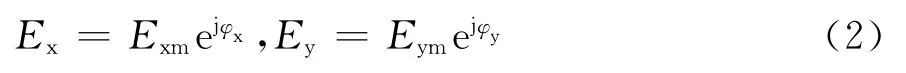
当两个分量的相位φx、φy和振幅Exm、Eym满足不同关系时,E的极化状态将是不同的。
2 电磁波极化实验原理
假设一个均匀线极化平面波,其电场强度振幅为E,从空气向一个无限大理想介质薄板平面斜入射,如图1所示。设入射角为π/4,并假设该极化波的极化面可以转动,入射面与极化面之间的夹角为α,该线极化波可分解为垂直极化波和平行极化波。当该平面波斜入射到理想介质平面时,分成两束波。
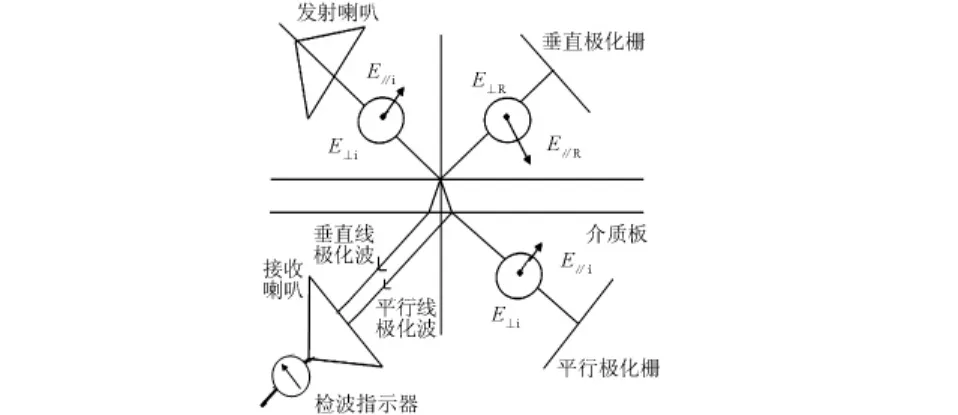
图1 电磁波极化原理图
一束为反射波,这束波到达垂直极化栅,平行极化波穿过极化栅,被后面的吸波材料吸收,垂直极化波被反射回来,在介质板上再次发生反射和透射,透射波到达接收喇叭天线,这一透射波为垂直线极化波。极化栅也称为极化栅网,极化栅分为垂直极化栅和平行极化栅。平行极化栅使平行极化波反射,而使垂直极化波通过,起到了极化滤波作用。而垂直极化栅使垂直极化波反射,而使平行极化波通过,起到了极化滤波作用。
另一束波为透射波,这束波到达平行极化栅,垂直极化波穿过极化栅被后面的吸波材料吸收,平行极化波被反射回来,在介质板上再次发生反射和透射,而反射波到达接收喇叭天线,这一反射波为平行线极化波。到达接收喇叭的是两个同频的正交的线极化波。
到达接收喇叭的垂直线极化波和平行极化波都经历了两次反射和一次透射,在忽略二次以上反射折射条件下,在接收喇叭处垂直极化波振幅为E⊥=EiΓ⊥τ⊥1τ⊥2cosα,平行极化波的振幅为E‖=EiΓ‖τ‖1τ‖2sinα,Γ⊥、τ⊥1、τ⊥2为垂直极化波的反射系数和透射系数,Γ‖、τ‖1、τ‖2为平行极化波的反射系数和透射系数。
由上分析可知,在入射波和介质参数确定的情况下,两个分量的振幅仅与角α有关,改变α的大小,即可调整电场E的x分量和y分量振幅大小。若要求E‖=E⊥,可得
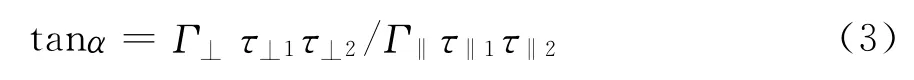
当入射角θ=45°时,

当介质是玻璃时,可得α=50°~60°,除满足一定的振动条件外,要得到要求的极化波,还要能调节两个分量的相位差,这可通过调节两个分量的行程差,即改变两个极化栅到微波分光仪转台中心的距离来实现。
由上分析可知,通过转动入射波的极化面(即改变角α的角度),可调节两个分量的振幅,通过调节两个分量的行程差Δl来调节两个分量的相位差Δφ=kΔl,从而可以得到各种极化波。
实验中的发射和接收天线为角锥喇叭天线,角锥喇叭天线由与喇叭相连接的矩形波导馈电。喇叭天线辐射的电磁波的电场方向与喇叭天线的窄边平行。当改变喇叭转角时,辐射的线极化电磁波可分解为两个正交的线极化波,满足电磁波的极化实验要求。
3 改进后的实验数据
用直流微安表作检波指示仪器时,在电磁波的圆极化和椭圆极化实验中,读数在6微安左右变化,实验现象很不明显。改用数字万用表后比较容易的测得实验数据,且实验现象比较明显。
1)接收圆极化波
转动发射喇叭天线的极化面,实现接收喇叭天线处垂直极化波和平行极化波幅度相等。移动可动金属极化栅,使垂直极化栅和水平极化栅到接收喇叭的距离满足条件,实现相位差90°的要求,形成圆极化波。转动接收喇叭天线,每转动15°,记录一次数字万用表的读数。从测量结果可以看出,数据基本都在很小范围内变化,合成波可看作圆极化波。
2)接收椭圆极化波
移动可动金属极化栅,可使垂直极化栅和水平极化栅到接收喇叭的距离满足条件即可形成椭圆极化波。转动接收喇叭天线,每转动15°,记录一次数字万用表的读数。从测量结果可以判断合成波为椭圆极化波。为了实现测量结果的可视化,我们可通过Matlab语言的对测量数据进行处理。
4 利用Matlab实现测量数据可视化
Matlab的图形功能主要包括数据可视化、创建用户图形界面和简单数据统计处理等。其中,数据的可视化不仅仅是二维的,还可以在三维空间展示数据,而数据或图形的可视化也是进行数据处理或者图形图像处理的第一步骤[4]。
通过借助Matlab语言编程对以上实验数据进行处理,可以更直观的显示出实验现象。由于接收喇叭的转角和测量值之间是极坐标关系,因此利用Matlab语言的绘制极坐标图二维绘图函数polar,对测量数据进行了可视化处理。从图2可以看出电场强度矢量端的变化轨迹近似是一个圆,随着测量数据的密集,连线会更加光滑。从图3可以看出电场强度矢量端的变化轨迹近似是一个椭圆。并给出了椭圆度。
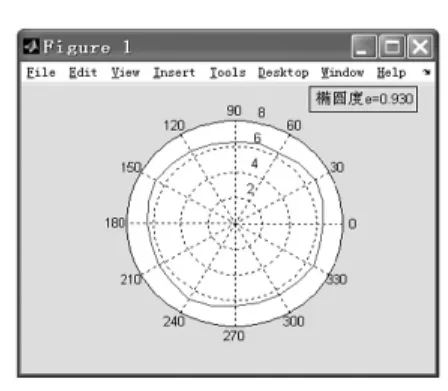
图2 圆极化测量数据

图3 椭圆极化测量数据
[1]代大海等.电磁波极化变换的数学原理及其性质[J].北京:中国科学G辑2008年第38卷第10期
[2]王被德,电磁波的极化及其应用[J].河南:电波科学学报,1999年9月,第14卷第3期
[3]谢处方,饶克谨,电磁场与电磁波(第四版)[M].北京:高等教育出版社,2006
[4]张威,Matlab基础与编程入门[M].西安:西安电子科技大学出版社,2004
