差分放大电路输入电阻的合理计算
2011-03-21黎嘉明
黎嘉明,张 林
(华中科技大学 电气与电子工程学院,湖北 武汉 430074)
1 问题的引出
图1所示是一种简单差分电路的原理图。如果在理想的运算放大器1端加电压激励ui1,2端加电压激励ui2,则由虚短虚断得up≈un,ii≈0。则有

由此可以解得

将up=un=i2iR3=R3ui2/(R2+R3)代入式(1)有

式(3)和式(4)即是输入电流i1和i2与ui1和ui2的关系[1]。
我们关心的问题是求取差电路的输入电阻Ri。
回顾电路理论中对输入电阻的定义:输入电阻是端口电压和端口电流的比值[2]。在定义里面需要明确端口条件。如图2所示,一个网络有两个端子1和2,那么当且仅当任意时刻均有i1=-i2时,才能组成端口,才能定义端口电流ii以及端口电压ui,进而才能够定义输入电阻Ri=ui/ii。
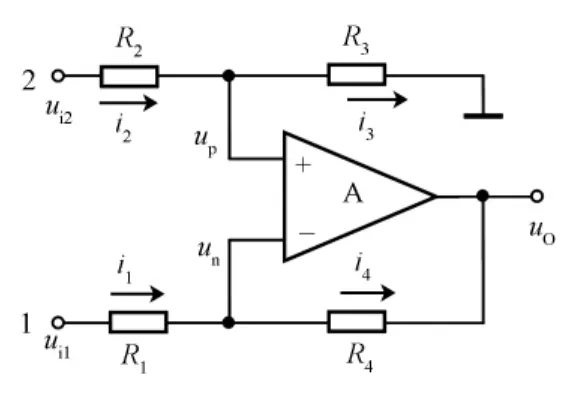
图1 差分放大电路
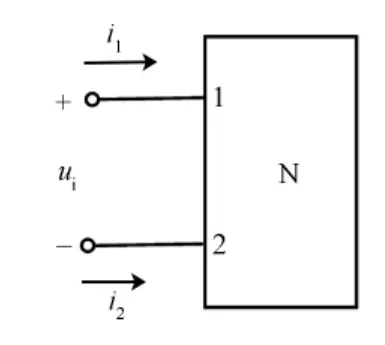
图2 二端口网络
从式(3)和式(4)可知,即便电路是高度对称的,i1=-i2仍然不成立,所以端口条件不成立。也就是说在激励源ui1和ui2作用下,无法直接获得图1差分放大电路的输入电阻。
唯一合理可行的方法是:在激励源ui1和ui2分别作用于1端和2端时,电路可看成一个双端口输入和单端口输出的网络。即把接地端看作隐含的公共端子,分别定义出两个输入电阻。
但是,这种描述并不能准确地涵盖单个激励源跨接在1和2两个端子之间的输入情况,因为此时ui2和ui1并不像双端输入那样是相互独立的。
2 两种输入方式及其本质差别
为了解决上述问题,我们将差分电路的几种激励接法全部画出,如图3和图4所示。
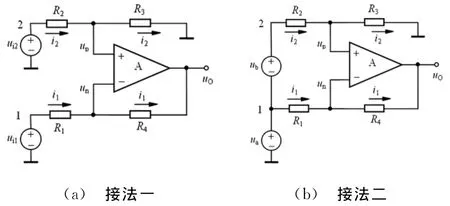
图3 差分电路双激励源输入的接法
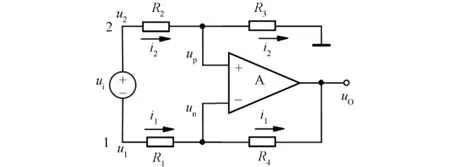
图4 差分电路单激励源输入的接法
图3中的两种接法实际上可以看作同一类输入方式(只要ua=ui1,ub=ui2-ui1),而图4则看作另一类方式。因这里的电压源没有接地端,即便把图3(b)中ua置零,图4与图3(b)仍然分属两种不同的输入形式。
我们把图3的输入方式称为“接地输入”,图4称为“悬浮输入”。我们按求解电路的思路对比两种接法的特点,如表1所示。

表1 两种接法的特性比较
由此可见,输入方式的差别改变了电路变量的确定与被确定的关系。
式(3)和式(4)的导出是以ui1和ui2为条件的,为各端子独立电位决定电流大小的方式,得到的结论:i1=-i2是不成立的。故只能看作两个输入端口,分别定义输入电阻(这里的i1= -i2不成立仅仅是不恒成立)。
对于悬浮输入方式而言,是以i1= -i2作为一切的前提,各端子独立电位并不确定,要由电流关系和电位差决定独立电位。此时两个端子被强制满足端口条件,从而自然可以定义它们之间的输入电阻。
综上所述,接地输入和悬浮输入方式的本质差别是端子独立电位和端子电流大小何者是决定方的差别,继而两者输入电阻的定义会完全不同。而在习惯上,笼统地说一个差分电路的输入电阻时,通常是指“悬浮输入”状态下的输入电阻,即差分电路的差模输入电阻。
3 输入电阻的正确求解
1)悬浮输入的输入电阻
对于图4所示的情形,基本方程如下:
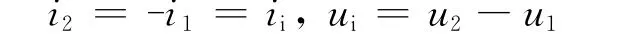
对应的实际求解方程组为(基本方程附加虚短虚断):

解得ui=ii(R1+R2),故有

由上文所述,此电阻是图4差分放大电路的输入电阻。
下面计算两端子此时的电位:
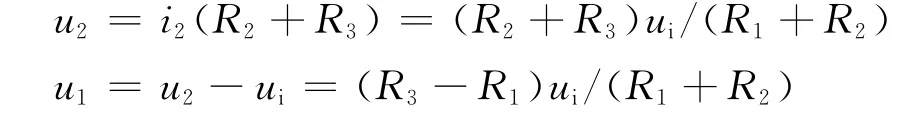
可以看到,u1和u2是按比例分配的。
把ui2=(R2+R3)ui/(R1+R2),ui1=(R3-R1)ui/(R1+R2)代入本文第一部分的式(3)和式(4),得
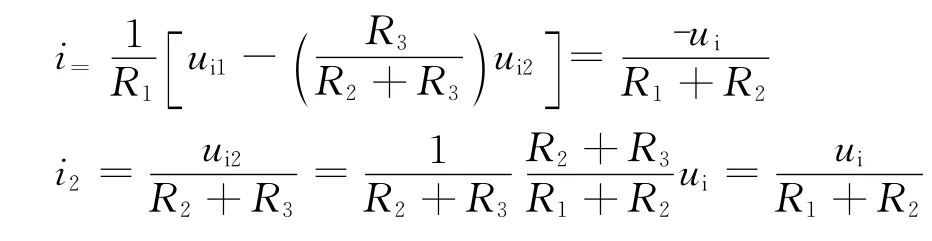
则i1=-i2成立。由此可以这样认为:悬浮输入方式导致两端子电位保持一个特殊比值,不能任意改变,因而自然地保证了输入电流的端口条件。
2)接地输入的输入电阻
对于图3(a)的情形,基本方程如下:

由第一部分的式(3)和式(4)可得到两个端口的输入电阻如下:
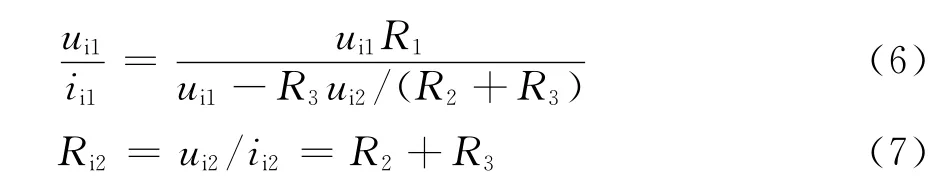
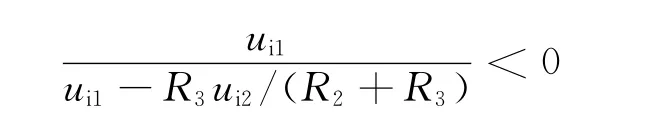
4 结语
由本文分析可知:图1中1、2两端分别对地的输入和单激励源跨接在1、2之间的输入实际上是两种完全不同的输入方式,它们的输入电阻是需要区别讨论的。即在求输入电阻时,应当首先明确激励源的输入方式,在不明确端子独立电位和电路电流约束条件中谁是决定方的情况下,无法准确定义输入电阻。
一般教材中差分电路的标注多采用图5(a)的形式[1],在两个端子处明确地标注出ui1和ui2,表示两个端子各自到地的电位(电压)。从强调电路输入端求差的角度而言,这种标注无可厚非,但在不加说明地求解差分输入电阻时,这种标注可能带有误导性:如果输入为“悬浮输入”的形式,端子1和2各自的独立电位要由整个电路决定,这与在1端和2端到地之间分别加激励源的效果完全不同。所以,在求差分输入电阻时,采用图5(b)的标注形式会更为确切。
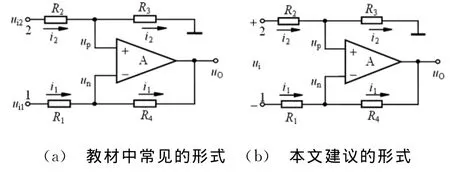
图5 差分电路的标注
[1]康华光主编.电子技术基础 模拟部分(第五版)[M].北京:高等教育出版社,2006,34-35
[2]颜秋容,谭丹.电路理论[M].北京:电子工业出版社,2009,330-331
