球体建模技术的研究与实现
2011-03-19康凤娥孔令德
康凤娥,孔令德
(太原工业学院电子工程系,山西太原030008)
真实感图形绘制是计算机图形学的一个重要组成部分。综合利用几何学、物理学、计算机科学等知识在显示器上生成像彩色照片一样的真实感图形。其中,球体的几何描述直接影响了图形的准确性和绘制的时间消耗,在绘制对称球体时,选择合理有效的数学模型尤为重要[1]。绘制球体时,首先对球体表面进行网格划分,可以使用三角形小面片或四边形小面片逼近。球体有两种建模的方法:地理划分法和递归划分法。地理划分法使用经纬线将球体表面划分为经纬网格。北极和南极采用三角形小面逼近,其它部分采用四边形小面逼近。使用地理划分法绘制的球体线框模型,两极小面较小,离赤道越近小面越大。旋转球体后露出了南北极点,破坏了球体的对称性。地理划分法除了用于绘制地球外,不能用于绘制足球等对称球体。游戏中绘制足球的一般方法是先在3DS中建模,然后导入场景中驱动,这种方法没有涉及对足球的建模算法。本文基于Bucky球体模型,使用递归划分法建立了足球模型。
1 平截正二十面体顶点绘制足球
足球模型是一个对称的球体,由12个正五边形和20个正六边形组成,共有60个顶点。假设把正二十面体的每条边三等分,每条边上生成两个新的顶点。因为正二十面体有12个顶点 (每一顶点有5条边),平截它之后产生12个正五边形。原有边长的1/3得以保留下来,有20个正六边形出现在新产生的正五边形之间,如图1所示。平截后的正二十面体完全对称,称为Bucky球[2],其形状与足球非常类似。Bucky球模型的展开图如图2所示。图中三角形内的数字的代表面编号,三角形外数字的代表顶点编号。注意到原有的正二十面体顶点在生成五边形面的过程中被裁平截掉了,使用三角形外的数字代表了Bucky球的五边形面编号。以三角形外的10号数字为例,代表了第10个五边形面编号(五边形面共12个,从0开始编号)。

图1 顶点平截后的正二十面体

图2 Bucky球展开图
设t为三维线段的等分比,可以计算正五边形顶点(x,y,z)顶点坐标,如图3所示。
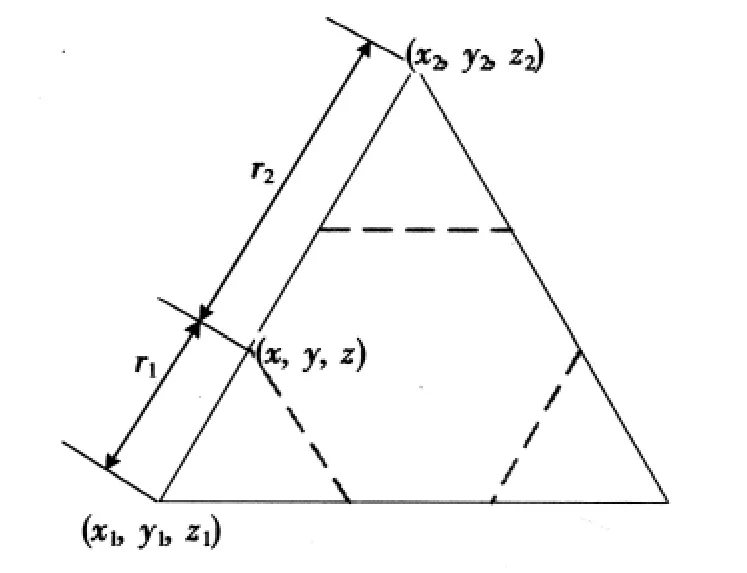
图3 计算三维线段等分点


图2中第10号五边形面各顶点依次是10-11、10-7、10-0、10-1、10-9各线段中靠近10的线段端点。简写成F10:11,7,0,1,9(50~54)括号中的数字代表给F10各顶点的编号(从F0~F12共5*12=60个顶点编号从0~59)。以F代表五边形的面,S代表六边形面,则Bucky球点表及五边形面表 (逆时针排列)见表1。
图2中六边形与五边形共享Bucky球顶点。三角形内的数字代表六边形的面编号。以S8号六边形面为例,由三角形外数字10-0、0-1、1-10围成的三角形中,每个边三等分的中间部分构成。在10-0线段上,F10中与0号点相交的顶点编号为52。同样F0中与10号点相交的顶点编号为4。依次类推构成S8号六边形面的各顶点编号是52,4,3,6,5,53。 简写成 S8:52,4,3,6,5,53。六边形面表见表2。

表1 点表及五边形面表
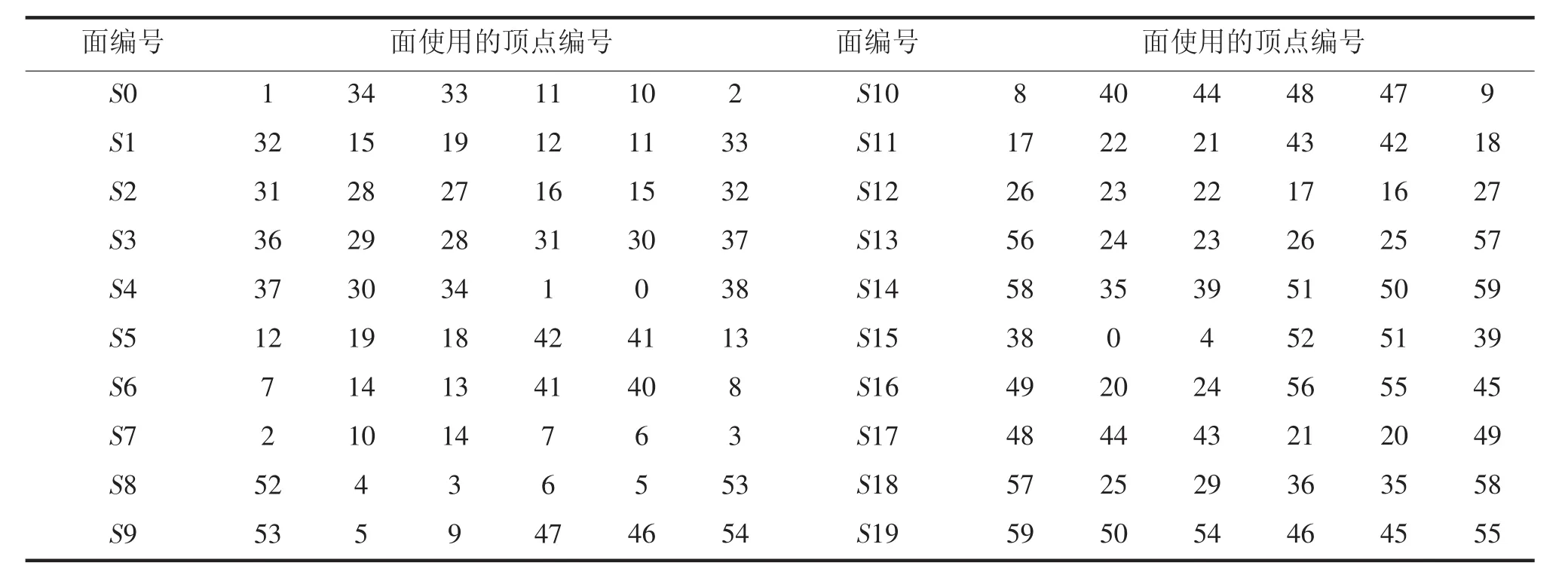
表2 六边形的面表
2 绘制真实感足球
对图1所示Bucky球施加光照后,绘制为光照对称球体。此时Bucky球的每个正五边形和正六边形表面全部由平面构成,而足球是由曲面构成,即需要对Bucky球的多边形表面进行“球化”处理。根据Loop细分方法[3],将正五边形平面和正六边形平面首先进行三角形“精化”处理,在此基础上进行“平滑”处理,即将中点拉到球面上形成足球线框模型,如图4所示。再对光照足球使用Phong明暗处理,并调整足球的材质后,绘制的真实感足球如图5 所示[4-5]。

图4 正五边和正六边形细分

图5 调整材质后的真实感足球
3 结论
对球体建模技术进行了研究。球体建模技术分为两种:地理划分法和递归划分法。使用地理划分法固定了二点分别做为南北极,使得靠近南北极的地方三角形越细,有聚集的趋势,而靠近“赤道”的地方三角形面积越大,有扩散的趋势。地理划分法绘制的球体更像一个地球,不适宜于绘制对称球体。使用递归划分法可以完成如足球等对称球体的绘制任务。本文通过对正二十面体进行顶点平截形成Bucky球,然后扩展平截面的中心点模长为球体半径,形成足球线框模型。调整材质和光源绘制了真实案足球。本研究成果所绘制的光照足球可以直接应用于球类游戏的开发过程中。
[1]孙洪军,杜道生,李争航.关于地球形状的三维可视化研究[J].武汉测绘科技大学学报,2000,25(2):158-162.
[2]Francis S hill Jr,Stephen M Kelley.计算机图形学(OpenGL版)[M].3版.胡事民,刘利刚,译.北京:清华大学出版社,2009:2,253-259.
[3]Tomas Akenine-Moller,Eric Haines.实时计算机图形学 [M].2版.普建涛,译.北京:北京大学出版社,2004:297-299.
[4]孔令德.计算机图形学基础教程(Visual C++版)[M].北京:清华大学出版社,2008:192-194.
[5]孔令德.计算机图形学实践教程(Visual C++版)习题解答与编程实践[M].北京:清华大学出版社,2010:275.
