改进遗传算法求解TSP问题的M atlab程序设计

缪桂根,高羽佳

(安徽农业大学信息与计算机学院物流工程系,合肥 230036)

改进遗传算法求解TSP问题的M atlab程序设计

缪桂根,高羽佳

(安徽农业大学信息与计算机学院物流工程系,合肥 230036)

用改进遗传算法求解TSP问题,并编制了完整的Matlab程序予以仿真实现.程序中选择算子采用最佳个体保存与赌轮选择相结合的策略,最后分析了最佳个体保存比例对寻优效果的影响.

改进遗传算法;TSP问题;Matlab程序

0 引 言

旅行商问题(Traveling Saleman Problem,TSP),又叫货郎担问题,是最基本的路线问题,该问题是在寻求单一旅行者由起点出发,通过所有给定的城市之后,最后再回到原点的最小路径成本.该问题具有广泛的应用性,如物流中的配送车辆调度问题就可看成一个约束性多路旅行商问题.因此,对TSP问题求解具有一定的现实意义.

TSP问题属于组合优化问题,随着问题规模增大,其可行解空间也急剧扩大,有时在当前的计算机上用枚举法很难甚至不能求出最优解,而用启发式算法求解这类问题的满意解是一个很好的方式,遗传算法就是寻求这种满意解的最佳工具之一.遗传算法模拟自然进化过程来搜索最优解[1],其本质是一种高效、并行、全局搜索的方法.本文采用遗传算法求解 TSP问题并编制Matlab程序进行仿真试验.

1 TSP问题的数学模型

TSP问题即寻找一条最短的遍历n个城市的最短路径,使得:

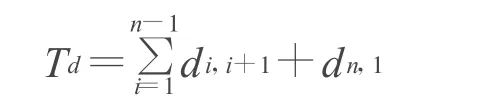
取最小值,di,i+1表示两城市i和i+1之间的距离.

2 遗传算法的运行过程

遗传算法是一种"生成+检测"的迭代搜索算法,其运算流程可用图1来表示.

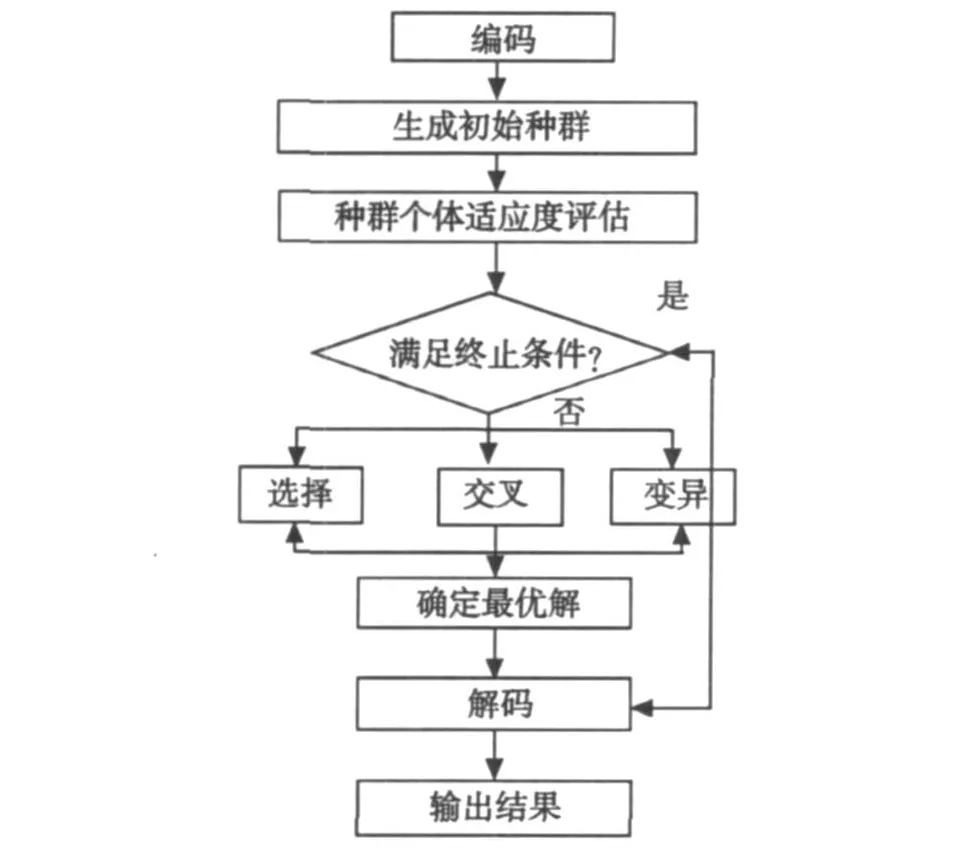
图1 遗传算法的程序

3 TSP问题的Matlab实现

参数说明:POPSIZE表示群体规模,NCITIES表示城市数目,pop表示初始种群,MAXGEN表示进化代数,Pc表示个体交叉概率,Pm表示个体变异概率.

3.1 编码并生成初始种群

编码是应用遗传算法时要解决的首要问题,也是设计遗传算法时的一个关键环节.求解TSP问题时,采用所遍历城市的顺序排列来表示各个个体的编码是最自然的编码方法[2],而且这种表示方法无需解码过程,占用的内存空间较小.

3.2 适应度评估

适应度用来度量群体中各个体在优化过程中达到或接近于或有助于找到最优解的优良程度.适应度较高的个体被选中遗传到下一代的概率较大;而适应度较低的个体被选中遗传到下一代的概率相对较小一些.本文用个体所表示的循环路线的倒数来作为适应度评估值,路线越短,个体适应度值越大.

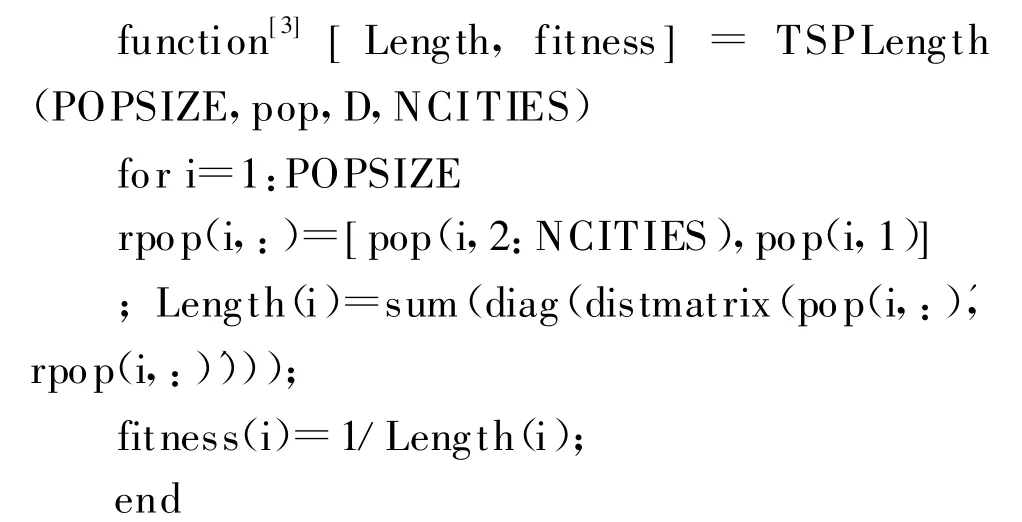
3.3 选择、交叉、变异

选择操作,是从群体中选择生命力强的个体产生新种群的过程.选择操作以个体的适应度评估为基础,其主要目的是避免有用遗传信息的丢失,从而提高算法的全局收敛性和计算效率.常用的选择算子有赌轮选择、联赛选择、最佳保留等.其中,最佳个体保存策略可保证迄今为止所得到的最优个体不会被交叉、变异等遗传操作所破坏,它是遗传算法收敛性的一个重要保证条件,但它也容易使得某个局部最优个体不易被淘汰反而快速扩散,从而使得算法的全局搜索能力不强,因此,最佳个体保存一般要与其他选择方法配合使用方可取得良好的效果[4].本文采用最佳个体保存与赌轮选择相结合的选择策略.其运行过程如下:对种群进行赌轮选择操作,找出当前种群中适应度最高的个体和适应度最低的个体;如果当前种群中最佳个体的适应度比总的迄今为止的最好个体的适应度还要高,则以当前种群中的最佳个体作为新的迄今为止的最好个体.用迄今为止的最好个体替换掉当前种群中的最差个体.此外,在每一代进化过程中也可保留多个较优的个体,直接将它们复制到下一代群体中.本文中用a表示最优个体保存的比例.

[pxLengthnow1,N1]=sort(Lengthnow);%由低到高排

[pxLengthnow2,N2]=sort(-Lengthnow);%由高到低排

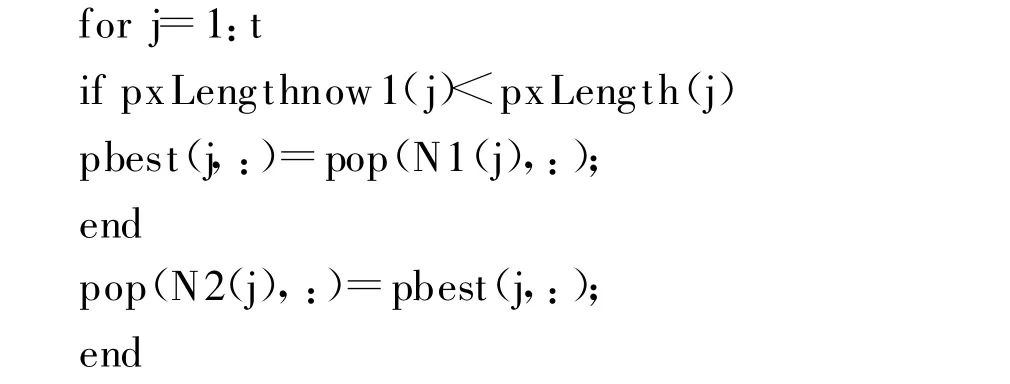
交叉运算产生子代,子代继承父代的基本特征.交叉算子一般包括两个内容:一是对种群中的个体随机配对并按预先设定的交叉概率来确定需要进行交叉操作的个体对;二是设定个体的交叉点,并对的部分结构进行相互交换.交叉算子的设计与编码方式有关.在TSP问题中几种有代表性的交叉算子如顺序交叉、类OX交叉等,这些交叉算子在产生新个体的过程中没有目的性,对于自然数编码的TSP问题,这些交叉可能破坏亲代的较优基因,从而使交叉算子的搜索能力大大降低.肖磊[5]等提出的受贪婪算法启发的使适应值上升的交叉算子,可以在很大程度上继承父代的优良基因,迅速优化适应值.本文采用该种交叉算子运算,该程序模块在其文中有详细描述,此处略.

变异操作是对个体的某些基因值做变动.变异操作的目的有两个,一是使遗传算法具有局部的随机搜索能力,当经过交叉操作群体已接近最优解领域时,利用变异算子可以加速向最优解收敛;二是使遗传算法可维持群体的多样性,以防止早熟现象.变异算子的设计也与编码方法有关,对于自然数编码的TSP问题,可采用逆转变异、对换变异和插入变异等.逆转变异,也称倒位变异,是指在个体编码中,随机选择两点(两点间称为逆转区域),再将这两点内的字串按反序插入到原位置中.倒位变异考虑了原有边的邻接关系,能将巡回路线上的优良基因性能较好地遗传到下一代,提高寻优速度.针对肖磊[5]等提出的贪婪倒位变异编制程序如下.

其中,距离矩阵D可由已知条件给出,也可根据给出的城市位置坐标编制程序计算.城市的位置坐标可编制程序随机产生.

4 仿真及结果

以文献[5]中提到的中国30个城市为例,城市坐标为W=[877;9138;8346;7144;6460;6858;8369;8776;7478;7171;5869;5462;5167;3784;4194;299;764;2260;2562;1854;450;1340;1840;2442;2538;4126;4521;4435;5835;6232].控制参数为:POPSIZE、NCITIES、Pc、Pm 可根据实际需要调整.主程序如下:

程序运行100次结果表明,有70次直接收敛到与最优解非常接近的解424.8693,平均在第23代左右就能收敛到最优解,程序运算时间平均在10 s左右.变异概率Pm可适当取大些,因为受贪婪算法启发的倒位变异是超适应值增加的方向发展.最佳个体保存比例a的选取对算法寻优会产生很大影响,比例过大,容易早熟,比例过小,解的质量不稳定.笔者对a的取值以0.05∶0.05∶0.3做实验,发现在a=0.10时,程序运算能取得最好的综合效果.

5 结束语

文章用改进遗传算法求解TSP问题,并编制了完整的Matlab程序予以仿真实现.程序中选择算子采用最佳个体保存与赌轮选择相结合的策略,最后分析了最佳个体保存比例对寻优效果的影响.遗传算法中遗传控制参数的选取对算法的影响很大,这些参数包括群体规模、编码长度、交叉概率和变异概率等.不同的问题各算子的影响程度不一样,因此,在实际运算时,要根据不同的问题进行参数的选择.

[1]雷英杰,等.M ATLAB遗传算法工具箱及应用[M].西安:西安电子科技大学出版社,2009:8-9.

[2]储理才.基于MATLAB的遗传算法程序设计及TSP问题求解[J].集美大学学报(自然科学版),2001,6(1):14-19.

[3]温清芳.遗传算法求解TSP问题的M ATLAB实现[J].韶关学院学报(自然科学版),2007,28(6):18-22.

[4]郎茂祥.配送车辆优化调度模型与算法[M].北京:电子工业出版社,2009:75.

[5]肖 磊,张阿卜,徐文进.用MATLAB求解 TSP问题的一种改进遗传算法[J].厦门理工学院学报,2005,13(4):38-42.

Matlab Programming for Solving TSP Based on Genetic Algorithm

MIAO Gui-gen,GAO Yu-jia

(Department of Logistics Engineering,School of Information and Computer,Anhui Agricultural University,Hefei 230036,China)

This article solves TSP with the improved genetic algorithm and compiles a complete set of Matlab procedures to be simulated.When it comes to reproduction operator,it adopts a joint strategy based on the best individual preservation and the roulette wheel selection.Finally,the article analyzes the effect on the optimization of genetic algorithm for TSP when the proportion of the best individual preservation takes different values.

improved genetic algorithm;TSP;matlab programming

TP391

A

1671-119X(2011)02-0042-04

2011-01-17

安徽农业大学青年科学基金资助项目(2009zr37)

缪桂根(1984-),女,硕士,助教,研究方向:物流系统优化、物流与供应链管理.