基于不动点算法和K2(m)剖分的遗传算法的改进
2011-03-17陈焕范志红高瑞贞张京军
陈焕,范志红,高瑞贞,张京军
(河北工程大学信息与电气工程学院,河北邯郸056038)
遗传算法是一类借鉴生物界自然选择与遗传机理的随机化搜索算法,具有简单,通用,鲁棒性强等特点,在函数优化、组合优化、自动控制、人工生命等领域得到了广泛的应用[1-4]。然而实践表明遗传算法仍然存在着一些不足,如局部寻优能力较差,存在早熟收敛问题,没有客观的收敛判断准则等[5-6]。经过对编码方式、控制参数的确定、选择方式和交叉机理等进行深入探究,并引入动态策略和自适应策略,在一定程度上提高了局部搜索能力,抑制了早熟现象[7-10]。然而针对遗传算法客观的收敛准则设计却并不多见,文献[11, 12]将不动点理论和遗传算法结合,尝试将种群个体的承载单纯形全部转化为全标单纯形作为收敛准则,分别采用K1剖分和J1剖分来求解函数优化问题。K2(m)剖分是比K1剖分和J1剖分更为精细的一种剖分[13],本文利用同胚映射将 n维闭包腔函数优化问题转化为n维标准单纯形不动点问题,对转化后的解空间进行K2(m)剖分,并与遗传算法结合,在客观的收敛准则下获得优化问题更精确的近似最优解。
1 不动点理论
不动点理论是最近几十年发展起来的高度非线性问题数值解的一种有效的方法。纯粹数学和应用数学的许多问题都可以归结为单纯形连续自映射的不动点问题。如优化函数 θ∶Cn→C是n维闭包腔Cn的一个连续自映射函数,向量 x*∈Cn使目标函数θ(x)达到极值的充要条件为▽θ (x*)=0。令F∶Cn→Cn,构造函数F(x)=x-▽θ(x),则求解θ(x)的零点问题转化为求解F (x)的不动点问题。然后通过对解空间进行适当的单纯剖分,对剖分顶点进行整数标号,利用标号信息从外部或边界人为始点沿转轴运算经几乎全标单纯形序列收敛到附近的全标单纯形,找到近似不动点。
本文利用同胚映射将求解n维闭包腔上函数F∶Cn→Cn的不动点问题转化为求解n维标准单纯形上函数f∶Sn→Sn的不动点问题,对转化后的解空间进行K2(m)剖分来求得优化问题的近似最优解。
2 K2(m)剖分理论
2.1 同胚映射

利用同胚映射将n维闭包腔连续自映射的不动点计算问题都可以转化成n维标准单纯形连续自映射的不动点计算问题。
2.2 K2(m)剖分

2.3 整数标号
设f∶Sn→Sn是的自映射,G是对Sn进行K2(m)剖分后的的一个单纯剖分,则对于每点 y∈G0,Sn的由f确定的整数标号函数为:l(y)=min {j∈N0|fj(y)≤yj>0,fj+1(y)≥yj+1},其中令n+1=0。
2.4 剖分网径
K2(m)剖分的剖分网径为

由式(1)可知,meshK2(m)与m成反比,只要取m足够大,就可以得到Sn的网径小于任何预先指定的正实数的K2(m)单纯剖分。
3 遗传算法的改进
在剖分区域中从一组随机初始点出发利用整数标号信息指导算法进行寻优,对种群进行反复的交叉、变异、选择等遗传操作,并对已走过的全标单纯形设置标志,以使种群经过有限代进化后达到包含全局最优解的状态。
3.1 编码
采用实数编码,形式如下:

其中,x=(x1,x2,1-x1-x2),x∈S2;f(x)—个体x的函数值,f(x)=Ax,f(x)∈S2,A为三阶矩阵;yi—个体的承载单纯形顶点;f(yi)—顶点yi的函数值;l(yi)—个体承载单纯形顶点yi的整数标号。
3.2 生成初始群体
对自映射f∶S2→S2进行K2(m)剖分,随机生成初始种群,计算种群中每个个体 x的函数值f (x),根据顶点标号函数l(y)计算每个顶点的整数标号l(yi),并将个体的适应度值定义为目标函数值3个分量的平方和。
3.3 交叉操作
交叉算子在遗传算法中起关键作用,是产生新个体的最主要方法,它决定了遗传算法的全局搜索能力。本文对父代种群施加交叉算子,操作如下:
(1)首先根据个体的承载单纯形顶点的标号将个体分类。顶点标号全部相同的为第一类,顶点标号不全相同的为第二类,顶点标号全不相同的为第三类,对于第三类个体不进行交叉操作直接进入下一代。

若交叉后得到的个体的承载单纯形的顶点标号属于第一类,则比较子代个体和父代个体的适应度值大小。若子代的适应度值高于父代的适应度值,则将其和父代适应度值高的个体遗传到下一代;若子代个体适应度值比父代都低,则将父代遗传到下一代,淘汰子代个体。
若交叉后得到的个体的承载单纯形的顶点标号属于第二类,则将子代个体和父代个体承载单纯形的顶点标号属于第二类的遗传到下一代,适应度值高的个体优先。
3.4 变异操作
变异算子作为主要的搜索算子保持群体的多样性。本算法对种群施加均匀变异,对非全标单纯形中的个体优先变异。
3.5 选择操作
每一代中的全标单纯形个体直接进入下一代种群,然后采用父子混合杰出者选择策略,以确保优秀基因继续遗传。
3.6 收敛判断准则
当种群中的个体的承载单纯形全部为全标单纯形时终止计算,输出全标单纯形对应的近似不动点。
4 算例分析
设群体规模为100,求下列问题的极小值。

其中,1≥x1≥x2≥0
步骤1:将函数的优化问题转化为求解不动点问题

θ(x)在点(0.675 00,0.425 00)处达到极小值,对应的函数值为-0.321 20。
步骤2:将求解C2上的函数F(x)的不动点问题转化为求解S2上的函数f(x)的不动点问题。
由于函数F∶C2→C2连续,则得到复合映射h°F°g∶S2→S2。即

步骤3:应用VC++编写程序,将转化后的解空间进行K2(m)剖分,生成初始群,对个体按照顶点标号进行分类,根据算法描述对种群反复施加交叉、变异、选择算子,直到满足收敛判断准则,并利用同胚映射将得到的不动点映射为优化问题的全局最优解。函数θ的全标单纯形分布如图1所示。
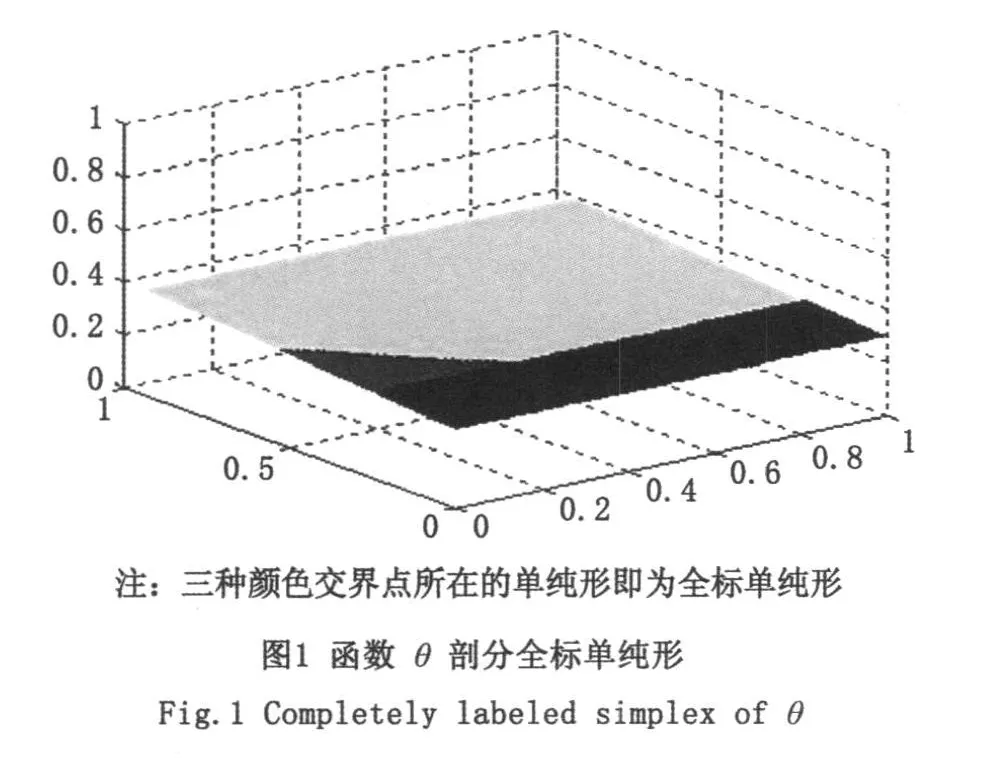
利用同胚映射g(x)=Px,x∈S2,将改进遗传算法得到的不动点映射到C2中。种群的初始代分布见图2-a,当m=4时,算法在6代收敛到全标单纯形,对应的全局极小点为(0.679 33, 0.421 662),函数值是-0.321 232(图2-b);当m=8时,算法在第4代收敛到全标单纯形,对应的全局极小点为(0.675 596 01,0.425 002),函数值是-0.321 250 0(图2-c),可以看出m值越大时,个体越集中。

5 结论
1)通过引入不动点算法和K2(m)剖分,可以使遗传算法具有客观的收敛准则,并获得近似最优解。
2)m值越大,剖分网径越小,得到的最优解越精确。
[1]陈琳,黄杰,龚正虎.一种求解最小诊断代价的小生境遗传算法[J].计算机学报,2005,28(12):2019-2026.
[2]刘习春,喻寿益.局部快速微调遗传算法[J].计算机学报,2006,29(1):100-105.
[3]周杰,王蕴恒,潘洪亮.基于遗传算法的小波神经网络DTC转速辨识[J].黑龙江科技学院学报,2009,19 (3):240-243.
[4]张春玉,赵延林,陈勇.混合变量遗传算法在预应力网架结构中的应用[J].黑龙江科技学院学报,2009, 19(4):306-309.
[5]朱朝艳,王建设,王学志,等.改进遗传算法的研究现状分析[J].吉林水利,2010(7):1-4.
[6]王莉.遗传算法的收敛性统一判据[J].自动化技术与应用,2001,23(6):16-19.
[7]王小平,曹立明.遗传算法——理论、应用与软件实现[M].西安:西安交通大学出版社,2002.
[8]GOLDBER G D E.Genetic algorithms in search,optimization and machine learning,reading.[M].New York:Addision -Wesley Publishing Company,inc.,1989.
[9]张京钊,江涛.改进的自适应遗传算法[J].计算机工程与应用,2010,46(11):53-55.
[10]刘立民,潘伟,庞彦军,等.多阶段复合型遗传算法的结构及性能研究[J].河北工程大学学报(自然科学版),2010,27(2):107-112.
[11]DONG Y Z,ZHANG J J,GAO R Z,et al.An improved genetic algorithm based on hk1 Subdivision and fixed point theory[C]//WANG S Y,YU L A,WEN F H,et al.Proceedings the second International Conference on Business Intelligence and Financial Engineering.Beijing:IEEE Computer Society Press,2009:222-230.
[12]王红霞,高瑞贞,张京军.基于不动点理论的改进遗传算法[J].河北工程大学学报(自然科学版),2010, 27(3):100-103.
[13]王则柯.单纯不动点算法基础[M].长沙:国防科技大学出版社,1993.
