基于小波变换的稠油出砂信号去噪分析★

李兵祥，樊超，张维娜，张微

（1 西安石油大学，陕西 西安 710065；2 陕西青年职业学院，陕西 西安 710068）

0 引言

石油生产过程中，出砂不仅导致设备损伤、产量下降，而且还会影响到油气井的寿命。采取合理的防砂、治砂措施是石油工作者面临的重要课题。出砂监测是评价防砂治砂效果的直接方法，也是优化生产，调整开采方案的依据。但目前国内还没有出砂监测装置，延长油气井寿命的生产决策，因此研究出砂监测技术具有重要意义，其关键是对通过传感器采集到的信号进行分析、处理，以获得准确的数据。由于受到流体噪声和电磁干扰信号的影响，必须对检测到的信号进行处理。传统的方法是傅里叶变换，但傅里叶变换是相对于全局时域或频域变换，无法表示时频局部特性。基于傅里叶变换的局限性，不适于处理非平稳信号。小波分析克服了傅里叶变换单分辨率上的缺陷，具有多分辨率的特点，在时域和频域都有表征信号局部信息的能力，时间窗和频率窗都可以根据信号的具体形态动态调整，低频部分可以采用较低的时间分辨率，而提高频率的分辨率，在高频情况下可以用较低的频率分辨率来换取精确的时间定位。通过室内试验及现场试验得到的数据显示小波变换能很好的去除噪声，并保存信号中的有用信息。经处理后的信号计算得出出砂量及出砂率，为防砂、治砂提供依据。

1 出砂信号的特征与滤波去噪方法的选择

1.1 出砂信号特性分析

出砂信号是由砂粒撞击输油管壁而产生的连续的尖峰脉冲式振动信号，是一种动态随机信号，由于砂粒撞击管壁是随机的、时有时无的，因此出砂信号具有随机性、脉冲性。并且该信号的频率范围在几十kHz～几百kHz，为超声波频带范围，而且信号的大小与流体的流速，砂粒浓度和砂粒的尺寸有关。当流体的流速、砂粒浓度、砂粒尺寸都比较大时，产生的出砂信号幅值很强；当流体流速、砂粒浓度、砂粒尺寸都比较小时，产生的出砂信号很弱。但是在流速非常小的情况下，即使砂粒很大，出砂信号都很弱甚至没有信号产生，这是由于在流速很低时，砂粒会出现沉积的现象，所以砂粒撞击管壁的几率就很少，以至于测得的信号很微弱或者无信号。

1.2 滤波去噪方法选择

经过放大后的信号夹杂着流体噪声及电磁干扰信号，必须进行去噪处理，滤波器的选择对去噪效果好坏起着非常重要的作用。

（1）维纳滤波器

维纳滤波器基本思想是寻找线性滤波器的最佳冲击响应或传递函数，使得滤波器的输出波形作为输入波形的最佳估计，即估计的均方误差达到最小。维纳滤波器的优点是适应面较广，无论平稳随机过程是连续的还是离散的，是标量的还是向量的，都可应用。对某些问题，还可求出滤波器传递函数的显式解，并进而采用由简单的物理元件组成的网络构成维纳滤波器。维纳滤波缺点是只适合于平稳过程不适合非平稳过程，而且输入过程的统计特性必须是已知的，但是输入过程取决于外界的信号、干扰环境，这种环境的统计特性常常是未知的、变化的，因而维纳滤波难以满足出砂信号去噪要求。

（2）卡尔曼滤波

卡尔曼滤波采用信号与噪声的状态空间模型，利用前一时刻的估计值和现时刻的观测值来更新对状态变量的估计，求出现时刻的估计值。只有在有用信号和干扰信号的频谱没有重叠的情况下，才能把有用信号和干扰信号完全区别开来。但是对于出砂信号，有用信号和干扰信号是重叠的，因此卡尔曼滤波不适合于出砂信号去噪。

维纳滤波与卡尔曼滤波不适合用于出砂信号去噪，因而选择小波变换。小波变换是一种时间—尺度分析方法，在时间、尺度（频率）两域都具有表征信号局部特征的能力，在低频部分具有较低的时间分辨率和较高的频率分辨率；在高频部分具有较高的时间分辨率和较低的频率分辨率，很适合检测正常信号中携带的瞬间反常现象并展示其成分。

2 小波变换在稠油出砂信号处理中的应用

2.1 小波去噪原理与过程

鉴于出砂信号的特点，在噪声处理上我们选择小波变换。小波去噪的基本思路就是用小波变换将含噪信号分解到多尺度中，然后在每一尺度下把属于噪声的小波系数去除，保留并增强属于信号的小波系数，最后重构出小波消噪后的信号。

一个含噪声的一维信号模型可以表示成如(1)的形式：

s（i）=ƒ（i）+σe（i），i= 0，1，…，n-1 （1）其中，ƒ（i）表示真实信号，e（i）表示高斯白噪声N（0，1），噪声级为1；s（i）表示为含噪信号。在实际工程应用中，有用信号通常表现为低频信号或一些比较平稳的信号，而噪声通常为高频信号。

对信号s（i）去噪的目的就是抑制信号中的噪声成分e（i），恢复出含噪信号中的真实信号ƒ（i）。

小波去噪的过程为：首先对信号进行小波分解，选择一个小波并确定一个小波分解的层次N，然后对s（i）进行N层分解；其次从第一层到第N层每一层高频系数选择一个阈值进行小波系数的量化处理；最后根据小波分解的第N层的低频系数和各层高频系数进行一维小波重构。在这3个步骤中，最重要的是如何选择阈值以及进行阈值量化，在某种程度上，它关系到信号去噪的质量。

2.2 阈值处理函数的选取

Donoho将阈值处理函数分为硬阈值和软阈值，设w是小波系数的大小，Wλ是施加阈值后的小波系数大小，λ是阈值。

（1）硬阈值：当小波系数的绝对值小于给定的阈值时，令其为0，而大于阈值时，保持其不变，即：

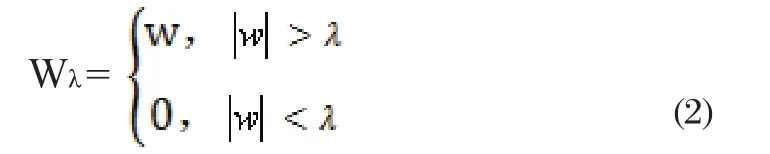
（2）软阈值：当小波系数的绝对值小于给定阈值时，令其为0，大于阈值时，令其都减去阈值，即：

两种阈值处理函数如图1所示。

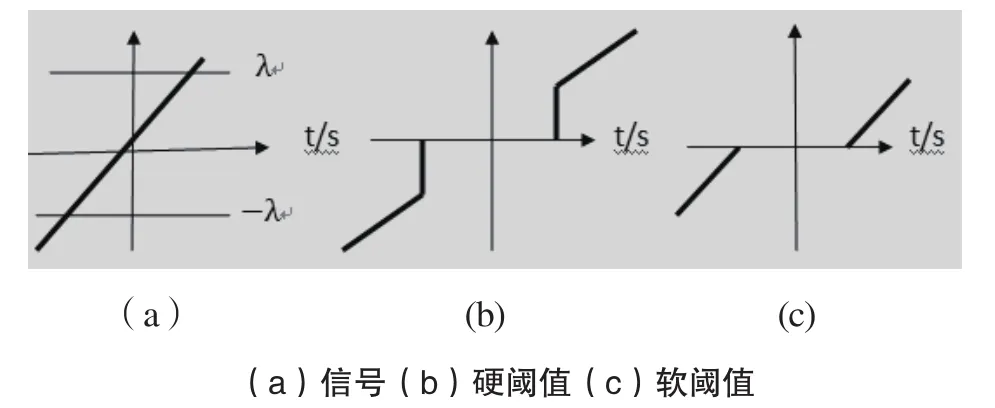
图1 两种阈值处理函数示意图

硬阈值函数能很好地保留信号边缘的局部特征，软阈值要相对平滑，但会造成边缘模糊的失真现象，本文采用软阈值进行信号处理。

3 信号的MATLAB仿真比较及实测出砂信号

为了验证小波去噪方法和傅里叶变换方法的去噪效果，在MATLAB上进行了仿真实验。通过MATLAB产生一个原始不含噪声脉冲信号和含白噪声的脉冲信号分别如图2和图3所示。在仿真中，分别对含噪信号进行傅里叶变换去噪和5层sym8小波基分解去噪，其图分别如图4和图5所示。

图2 不含噪声脉冲信号

图3 含噪声脉冲信号

图4 傅里叶变换去噪后的信号

图5 小波变换去噪后的信号

通过室内试验及现场试验实际测试通过传感器、放大滤波电路、小波去噪后的信号如图6和图7所示。

图6 实测小波去噪出砂信号

图7 实测小波去噪出砂信号

由图4、图5可以看出小波阈值去噪的效果确实优于傅里叶变换去噪，并且小波去噪很好的保留了原始信号中的尖峰和突变部分，而傅里叶变换进行滤波时，由于它不能将有用信号的高频部分和由噪声引起的高频干扰加以有效区分，使得滤波后的信号残留了大量的噪声。

4 结论

对于稠油出砂信号采用sym8小波基，进行5层分解，应用软阈值函数处理能够很好的滤除噪声，并保留了原始信号中的尖峰和突变部分，为后续准确的计算出砂量、出砂率奠定了基础。

[1] 方兴.小波分析及其去噪性能研究[J].浙江师范大学学报,2003.

[2] 孙延奎.小波分析及其应用[M].北京:机械工业出版社,2005.

[3] 戈斯瓦米.小波分析理论、算法及其应用[M]. 许天舟 译.北京:国防工业出版社，2007.

[4] 李晓峰，张国柱.小波变换思想及其在信号处理中的应用[J].电子科技大学学报，2008.

[5] 胡昌华.基于MATLAB的系统分析与设计——小波分析[M]. 西安:西安电子科技大学出版社，2008.

[6] 张德丰.小波分析与工程应用[M]. 北京:国防工业出版社，2008.

[7] 张德丰.MATLAB小波分析[M]. 北京:机械工业出版社，2009.

[8] 邸继征.小波分析原理[M]. 北京:科学出版社，2010.