超声速复杂流动中湍流模型的性能评估

赵 瑞 阎 超

(北京航空航天大学 航空科学与工程学院,北京 100191)

超声速复杂流动中湍流模型的性能评估

赵 瑞 阎 超

(北京航空航天大学 航空科学与工程学院,北京 100191)

对 8°,16°,20°,24°超声速二维压缩拐角进行了数值模拟,系统评估了 SA(Spalart-Allmaras),k-ω,SST(Shear Stress Transport)3种工程常用湍流模型对激波/边界层干扰复杂流动的模拟适用能力.对于“弱”干扰、小分离,工程常用湍流模型能够较准确地预测其压力、摩擦力、热流分布,而对于“强”干扰、大分离则会造成较大的偏差.同时,随着分离区的增大,各湍流模型的适用性能差别更加明显,数值方法也有一定的影响.

超声速流动;湍流模型;激波;边界层;计算流体力学

在超声速飞行器设计中,激波/边界层干扰等复杂流动会对飞行器局部产生严重的气动力、气动热载荷.目前对于该流动现象的模拟主要有直接数值模拟(DNS,Direct Numerical Simulation),大涡模拟(LES,Large Eddy Simulation)以及从雷诺平均 N-S方程出发的湍流模型理论 RANS(Reynolds Average Navier-Stokes).尽管 DNS和LES能够更为准确地刻画流动细节,但是需要海量网格,这对于工程实际问题,尤其对于超声速高雷诺数流动,是十分不现实的.RANS由于其易实现性,高性价比以及强鲁棒性一直是应用 CFD(Computational Fluid Dynam ics)解决工程湍流问题最实际、最有效的选择.

自 20世纪 70年代以来,国内外对激波/边界层干扰等复杂流动现象进行了大量试验和计算研究.在国外,文献[1-4]对压缩拐角进行系统的试验研究,并编制了高超声速激波/边界层干扰试验数据库;文献[5]采用 DNS方法对压缩拐角进行数值模拟,并分析了激波/边界层干扰机理.在国内,文献[6-7]采用多种先进湍流模型对高超声速基准流动进行模拟,得出了有价值的结论.值得注意的是,文献[8]中总结出采用 RANS模拟激波/边界层干扰具有以下 4种特点:

1)不能很好地预测逆压梯度的影响,计算所得压力抬升往往滞后;

2)分离区物面压力计算结果偏大;

3)再附点之后物面摩擦力与热流密度过高;

4)干扰区下游壁面处速度减小过快.

针对超声速激波/边界层干扰复杂流动,本文采用 3种工程常用湍流模型(SA[9]模型,k-ω[10]模型,SST[11]模型)对超声速压缩拐角进行数值模拟,研究各湍流模型对激波/边界层干扰复杂流动的模拟适用能力,同时系统评估全 N-S方程与工程常用薄层假设处理对模拟该复杂流动的影响,为进一步建立超声速复杂流动湍流模型的适用性评估体系奠定基础.

1 数值方法

1.1 控制方程

基本控制方程为雷诺平均 N-S方程,其守恒形式为

其中,τtij为雷诺应力,对于 μt不同的模化方法,构造不同的涡粘性湍流模型.

鉴于计算效率考虑,国内外绝大多数三维粘性流动计算软件均采用薄层 N-S方程,即忽略流向及其间的交互粘性作用,仅保留控制方程中沿物面法向的粘性项,这种处理虽然具有一定的物理基础并且大大提升了计算速度,但对于有分离的复杂流动,却有一定程度的精度损失.

1.2 湍流模型

湍流模型理论分为两大类:一类称为雷诺应力湍流模型,另一类称为涡粘性湍流模型.涡粘性湍流模型由于形式简单、鲁棒性好,在工程湍流问题中得到广泛应用.

本文所采用 3种涡粘性湍流模型描述如下:

SA模型:一方程湍流模型,从经验与量纲出发,只需求解一个涡粘性系数满足的输运方程,由于其构造简单,鲁棒性好,对壁面网格质量依赖小,该模型在工程界得到广泛应用.

k-ω模型:两方程湍流模型,求解湍动能以及它的比耗散率的对流输运方程,由于该模型不需要显式的壁面衰减函数,适用性较好.

SST模型:两方程湍流模型,是 k-ε模型与 kω模型的混合模型,由于该模型保持了 k-ω模型近壁面特性,同时保持了 k-ε模型在尾迹区的特性,使其在工程界应用广泛.

2 计算结果及分析

为考察上述 3种湍流模型零压梯度下模拟边界层的能力,本文首先选择超声速平板算例.然后对超声速二维压缩拐角(8°,16°,20°,24°)进行计算,随着拐角增大,激波/边界层干扰程度由弱变强,分离区从小变大,从而系统考核各湍流模型的性能.

2.1 超声速平板算例

文献[12]采用 DNS方法对超声速平板进行数值试验.试验条件为:Ma∞=2.25,Re=635 000 in-1.

计算结果如图 1所示,在零压梯度下,无论在粘性底层还是在对数律层,3种湍流模型性能一致并与经验公式吻合良好,鉴于超声速可压缩效应的影响,3种湍流模型在对数律层与 DNS结果稍有差异.

图1 超声速平板速度型(x=8.8in)

2.2 超声速二维压缩拐角算例

文献[1-4]中在普林斯顿大学超声速风洞对二维压缩拐角进行一系列试验,试验条件如表1所示.

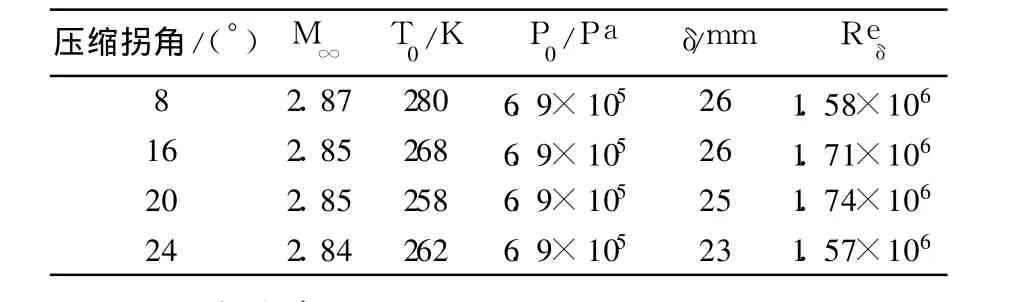
表 1 超声速压缩拐角试验条件

2.2.1 模型建立

压缩拐角干扰区流动特性受入口条件影响较大,本文通过反复调节拐角前端平板长度,保证来流在入口处与试验一致,计算模型如图 2所示.

4种拐角第一层网格高度都为 2.6×10-7m,保证 y+＜1,经过网格收敛性检验,4种拐角网格量均为100×240.

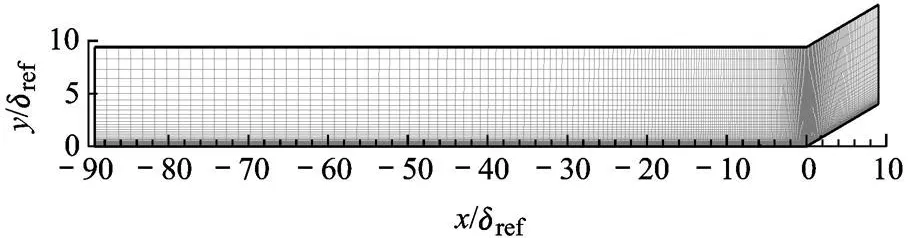
图2 16°拐角整体网格

2.2.2 流场分析

随着拐角度数的增大,拐角处激波/边界层干扰程度由弱变强,分离区也由小变大,流场现象随之不断丰富.以 24°拐角为例,超声速气流流至拐角前段时,在逆压梯度的作用下,边界层变厚,从而使主流提前产生一系列的压缩波,并在离拐角一定距离处汇聚成一道斜激波,激波后边界层往往不能承受强逆压梯度而发生分离,形成一个“凸包”,超声速气流流经该“凸包”后紧接着在斜面的压缩作用下,形成新的压缩波区,流动示意图如图 3所示.

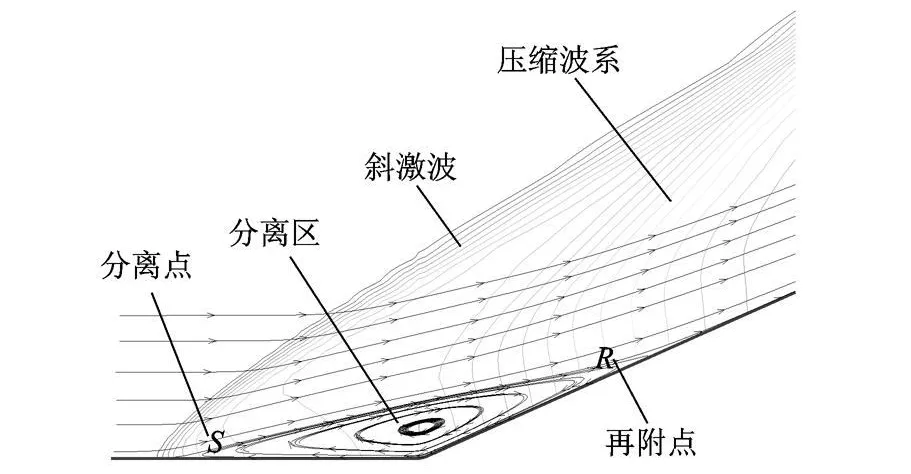
图3 激波/边界层干扰示意图

如表 2所示,3种湍流模型都没有很好地捕捉到分离点位置,而且再附点位置都要滞后.SA模型计算所得分离区最大,k-ω最小.使用 SST模型计算分离点最靠前,SA模型计算再附点最滞后.3种湍流模型,采用全 N-S方程计算,分离点均提前,再附点均滞后,从而分离区较大,结果对比如表 3所示.

表 2 各湍流模型分离区特性

表 3 各湍流模型分离区大小对比 %

2.2.3 壁面压力与摩擦力分布

分别采用全 N-S方程与薄层假设,使用 3种湍流模型对 8°,16°,20°,24°压缩拐角进行数值计算,计算所得压力 p/pref及摩擦力系数 Cf分布见图 4～图 7.

8°,16°拐角激波 /边界层干扰程度弱,分离区小,3种湍流模型所得压力分布基本一致,且与试验值吻合较好,而摩擦力差别较大:平板区 SA模型所得摩擦力最大,SST模型最小,再附区 k-ω计算结果与试验值吻合较好,SA,SST结果走势一致,但明显低估了摩擦力.

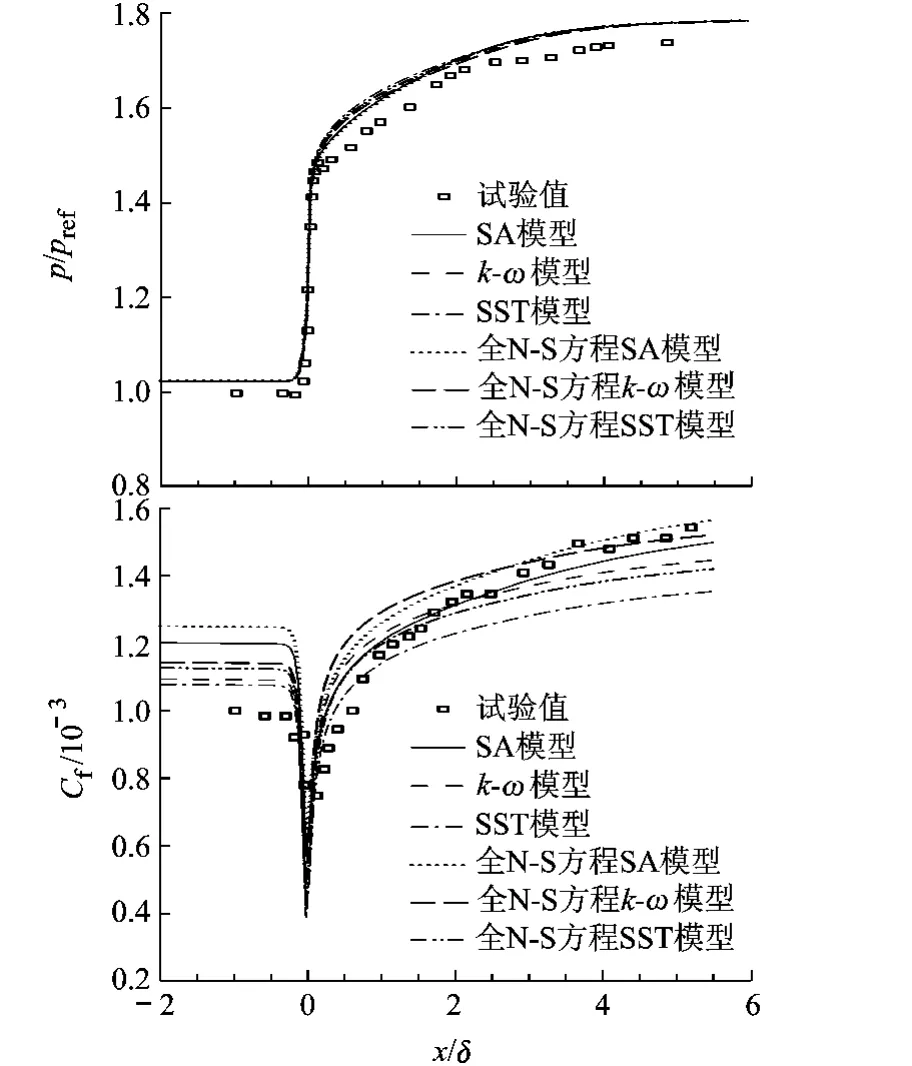
图4 8°压缩拐角壁面压力与摩擦力分布

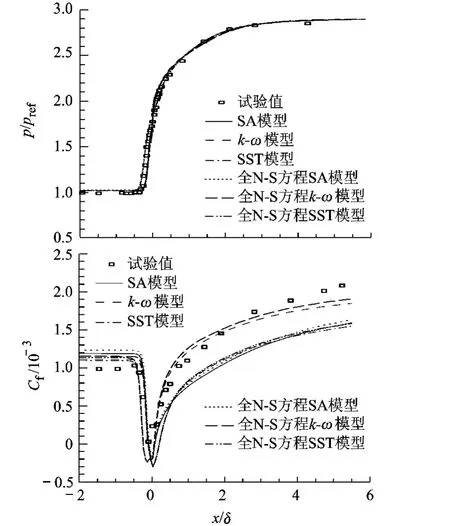
图5 16°压缩拐角壁面压力与摩擦力分布

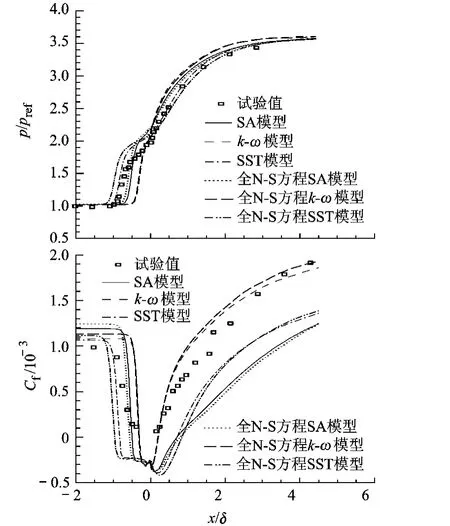
图6 20°压缩拐角壁面压力与摩擦力分布

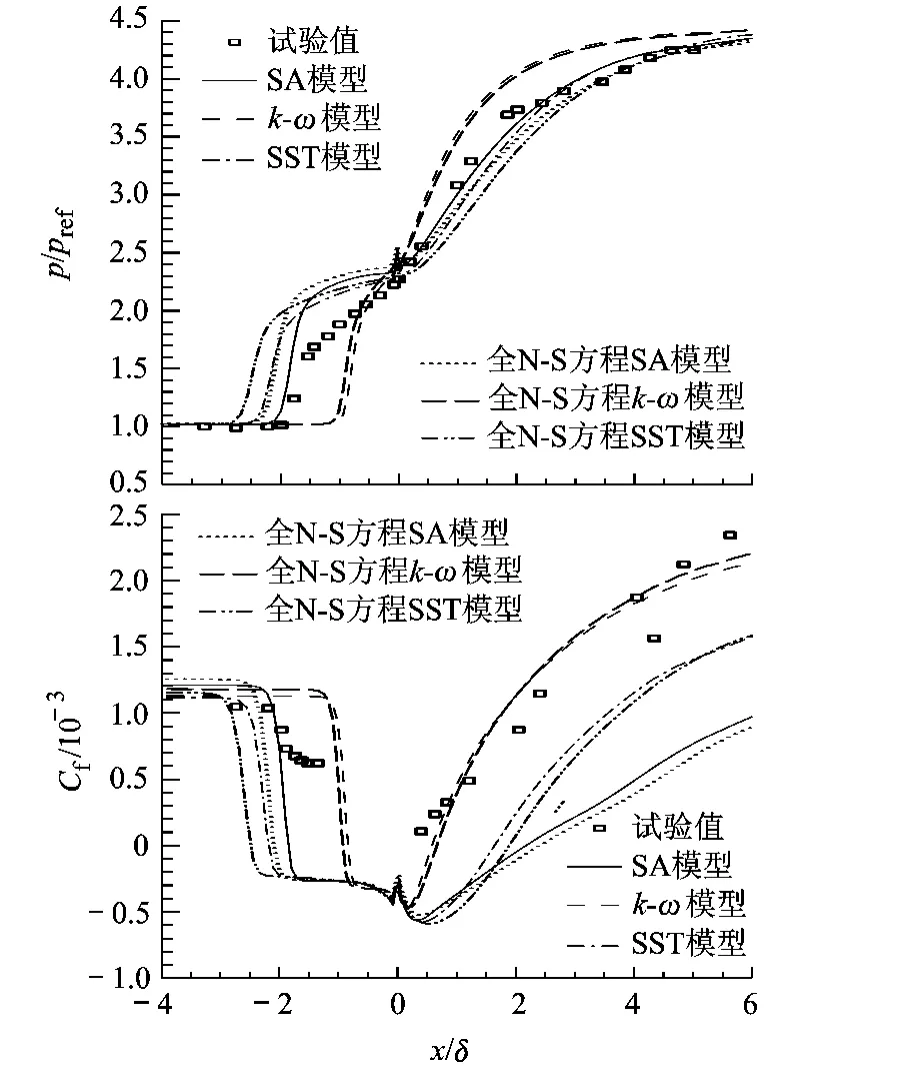
图7 24°压缩拐角壁面压力与摩擦力分布

20°,24°拐角激波 /边界层干扰程度增大 ,分离区也不断增大,3种湍流模型的适用能力也都有所下降.从压力分布来看,3种湍流模型都不能捕捉分离区的特性,在再附区,k-ω压力恢复过高,SA、SST压力恢复与试验一致.摩擦力的计算结果差异更加显著,k-ω能够较好地预测再附区的摩擦力,而 SA,SST皆低估了摩擦力,并且随着拐角角度的增大,SA模型的适用能力降低最快.

同时,对于压力计算来说,分别采用全 N-S方程与薄层假设计算所得结果只在有分离的情况下差别明显,而对于摩擦力计算,无分离情况下,全N-S方程计算结果较大,而有分离时则相反.

2.2.4 壁面热流分布

热流计算结果如图 8所示,3种湍流模型中,SST模型与试验值吻合最好,SA模型在分离区附近低估了热流,而 k-ω模型在整个再附区预测热流过高.同时可以看出,使用全 N-S方程计算,平板处热流计算值较高而再附区则正好相反.

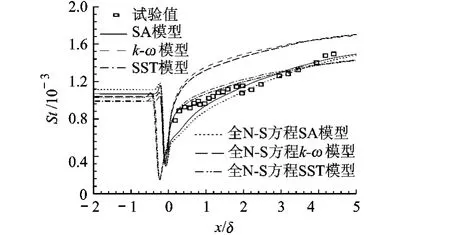
图8 16°压缩拐角壁面热流分布

3 结 论

本文采用 3种工程常用湍流模型对超声速二维压缩拐角进行了数值模拟,系统评估了上述湍流模型对激波/边界层干扰复杂流动的模拟能力.研究结果表明采用 RANS模拟激波/边界层干扰复杂流动,对于“弱”干扰、小分离能够较准确地预测其压力、摩擦力、热流分布,而对于“强”干扰、大分离就无法很好地捕捉分离点位置,进而对压力分布等造成较大的偏差.

与文献[8]结论有所不同,本文研究表明RANS模拟激波/边界层干扰的特点不能一概而论,各湍流模型的性能差别较大,数值方法也有一定的影响.

1)3种湍流模型在零压梯度下性能基本一致.

2)SA与 SST模型预测分离点提前,再附点滞后,分离区过大,而 k-ω模型预测分离点与再附点全都滞后,分离区过小.

3)SA与 SST模型分离区物面压力计算结果偏大,而 k-ω计算结果偏小.

4)SA与 SST模型再附点之后的物面摩擦力与热流密度计算结果偏低,而 k-ω计算结果偏高.

5)随着分离区的增大,SA模型的适用能力下降最快.

6)随着分离区的增大,流动变量的交叉项比重增加,使得全 N-S方程与薄层假设计算结果差异变大.

References)

[1]SettlesG S,Fitzpatrick T J,Bogdonoff SM.Detailed study of attached and separated compression corner flow fields in high Reynolds number supersonic flow[J].AIAA Journal,1979,17(6):579-585

[2]SettlesG S,Bogdonoff SM,Vas IE.Incipient separation of a supersonic turbulent boundary layer at high Reynoldsnumber[J].A IAA Journal,1976,14(1):50-56

[3]SettlesG S,Vas IE,Bogdonoff SM.Details of a shock-separated turbulent boundary layer at a compression corner[J].AIAA Journal,1976,14(12):1709-1715

[4]SettlesG S,Dodson L J.Hypersonic shock/boundary-layer interaction database[R].NASA-CR-177577,1991

[5]Martin M P,Smits A,Wu Minwei,et al.The turbulence structure of shock wave and boundary layer interaction in a compression corner[R].AIAA-2006-497,2006

[6]张红杰,马晖扬,童秉纲.高超声速复杂流动中湍流模式应用的评估[J].空气动力学报,2001,19(2):210-216 Zhang Hongjie,Ma Huiyang,Tong Binggang.Turbulence modeling validation in hypersonic complex flows[J].Acta Aerodynamica Sinica,2001,19(2):210-216(in Chinese)

[7]Yang Xiaodong,Ma Huiyang.Investigation of nonlinear turbulence models for separated supersonic flows[J].Acta Aerodynamica Sinica,2002,20(4):458-463

[8]Wilcox D C.Turbulence modeling for CFD[M].La Canada:DCW Industries,1994:203-205

[9]Spalart PR,Allmaras SR.A one-equation turbulence model for aerodynamic flows[R].AIAA-92-0439,1992

[10]Wilcox D C.Reassessment of the scale determining equation for advanced turbulencemodels[J].AIAA Journal,1988,26(11):1299-1310

[11]Meter F.Zonal two equation k-ωturbulencemodels for aerodynamic flows[R].AIAA-93-2906,1993

[12]Gao H,Fu D X,Ma Y W,et al.Direct numerical simulation of supersonic turbulent boundary layer flow[J].Chinese Physics Letters,2005,22(7):1709-1712

(编 辑 :李 晶)

Evaluation of engineering turbulence models for comp lex supersonic flows

Zhao Rui Yan Chao

(School of Aeronautic Science and Engineering,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)

Supersonic flows pasta series of two-dimensional compression ramps were simulated by employing three popular engineering turbulence models,namely Spalart-Allmaras(SA),k-ω,shear stress transport(SST).The performance of the three engineering turbulence models was evaluated and summarized.All three turbulence models are reasonably accurate to predict the surface pressure,skin friction and heat transfer distribution for“weak”shock/boundary-layer interactions,but show significantdis crepancies with experimental data for“strong” interactions.Each turbulence model shows much different simulation capability with the separation lengths increased,and the numerical method has much effect too.

supersonic flow;turbulence models;shock;boundary layers;computational fluid dynam ics

V 211.3

A

1001-5965(2011)02-0202-04

2009-12-23

国家 973计划资助项目(2009CB724104)

赵 瑞(1987-),男,山东阳谷人,博士生,zr8800@gmail.com.