直达滑模控制

姜玉宪 周尹强 赵 霞

(北京航空航天大学 自动化科学与电气工程学院,北京 100191)

直达滑模控制

姜玉宪 周尹强 赵 霞

(北京航空航天大学 自动化科学与电气工程学院,北京 100191)

用传统到达条件综合而成的滑模控制系统不能保证所有出发于滑动模态邻域的相轨线都能直接到达邻近的滑动模态分支,导致状态转移过程超调,这对于某些控制工程是不允许的.为使滑模控制过程单向收敛,提出了直达滑模控制方法.通过对传统到达条件表述中的不足的分析,介绍了直达函数的定义和直达条件的建立.直达条件是用直达滑模控制法综合滑模控制系统的依据.直达滑模控制系统由指令模态及开关型直达滑模控制组成.与传统到达条件不同,满足直达条件的控制,可保证所有出发于滑动模态邻域的相轨线都能直接到达邻近的滑动模态分支,沿滑动模态趋向零态,状态转移过程快速而无超调.将直达滑模控制应用于示例系统并进行仿真,仿真结果符合对直达滑模控制性能的预期.

滑模控制;到达条件;直达条件

滑模控制具有许多优点,也存在一些问题,例如滑模控制过程的非单向收敛性(或称之为超调).这对于某些控制工程是不允许的,例如飞机着陆、航天器对接、机器人装配等.现有研究认为,产生这一现象的原因有:①到达条件太简单,仅仅一个到达条件可能导致到达过程的正常运动段历时很长、超调量很大等不良品质[1],因而提出了“趋近律”的概念[1-2];②开关型滑模控制不连续,改进措施是把控制改为连续-开关混合型控制[3-4].此类研究收到了一定的效果,但未找到真正原因.滑模吸引区的研究与滑模非单向收敛有关,却未发现滑模非单向收敛与到达条件表述之间的联系[5-7].

经研究发现,滑模控制过程非单向收敛的产生是由于传统到达条件所选择的控制不能保证出发于滑动模态邻域的相轨线都能直接到达滑动模态的邻近分支,而是有的先离开邻近的分支、反向绕到另一个分支而后到达.此现象称之为绕达,绕达必然导致超调的出现.本文对绕达现象的成因进行了分析.由于直达无超调,是研究滑模控制系统综合所期望达到的目标之一.实现直达滑模控制的首要任务是建立直达条件.以直达条件为依据综合滑模控制系统的方法叫直达滑模控制.本文介绍了直达条件的建立、直达滑模控制方法和仿真结果.

1 相轨线的直达和绕达

滑模控制问题的被控对象是

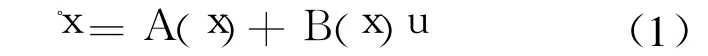
其中 x∈ Rn,其初值为 x(0)=x0,A∈ Rn×n,B∈Rn×m,u∈Rm是非连续且无界(依据需要任意界定)控制.滑模控制由 2部分组成,即滑动模态 s和控制 u.

1.1 滑动模态

通常 s是状态变量线性组合而成的函数等式:

式中,σ(x)为切换函数;C∈ Rm×n为 σ(x)的线性组合系数.式(2)给定后,C为常数.如滑模控制中被控对象为

假定期望的系统镇定动态过程是指数衰减的,则对应的 s是

依据 x(t)的渐近稳定性要求,c1的允许取值范围是:0≤c1＜∞.式(4)所限定的 x1和 x2的取值范围称为 s的存在区域,记作 Ω.根据x1可能变化的范围(例如:-2＜x1＜2)和对系统动态过程的要求,若指定 c1=0.5,则系统式(3)的 s定义为

它是 s的存在区域 Ω中斜对称于零点的两条线段sP和 sN,如图 1所示.图中 ΩNH为 s的邻域.

1.2 直达与绕达

u将 x从 x0拉到 s上的途径有两条:x10＞0将 x拉到 sP上,或 x10＜0将 x拉到 sN上,为直达;x10＞0将 x拉到了 sN上,或 x10＜0将 x拉到了 sP上,则为绕达.虽然它们都到达了 s,但动态过程x1(t)不同,直达过程中 x1(t)单向收敛无超调,绕达过程中 x1(t)有超调.直达还是绕达,取决于 u的选择方法.图 2为直达和绕达的相轨迹示意图.

图1 s的存在域和邻

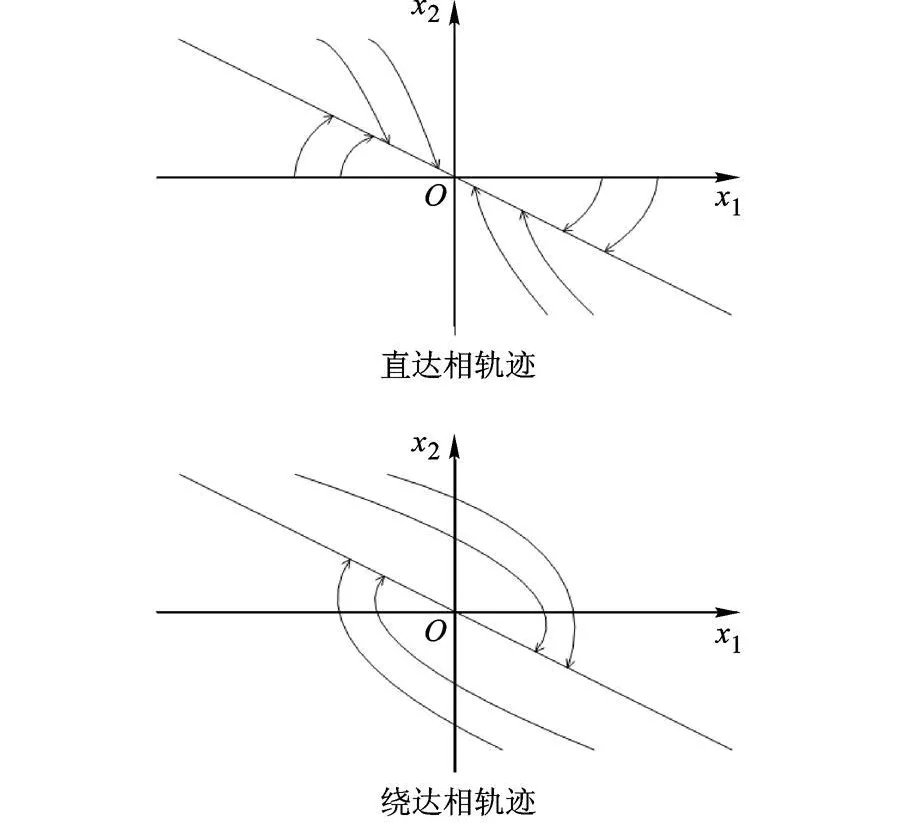
图2 直达和绕达的相轨迹示意图

1.3 传统到达条件下的滑模控制

依据传统到达条件:

选择u,在C为常数的前提条件下,有σ·(x)=Cx·,将式(1)中的x·代入得σ·(x)=CA(x)+CB(x)u.假定(CB(x))-1存在,开关型滑模控制u为

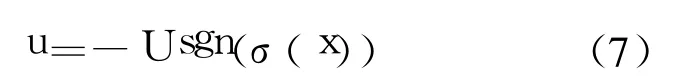
其中,U满足(CB(x))-1CA(x)⊂U的要求,sgn x为符号函数.

由式(7)的 u与式(1)形成了闭环滑模控制系统.

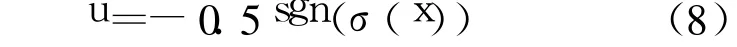
u与式(3)形成闭环滑模控制系统.

2 滑模控制的直达和绕达双重性

对于用传统到达条件综合出来的开关型滑模控制系统,从 s邻域中 x0出发的相轨线存在着直达和绕达 s的两种可能性,以下将复现这种现象并分析其产生的原因.

2.1 s的邻域

到达条件:

满足式(9)的 x0所在子空间叫 s的邻域,记作ΩNH.对式(3)系统,到达条件的有关公式为

因此,符合式(9)要求的 x0为 -2＜x10＜2,-1＜x20＜1,如图 1中的 ΩNH.

2.2 滑模控制系统的直达和绕达现象

表 1是式(3)系统 ΩNH中符合式(9)要求的 4个 x0及其对应的

表 1 s邻域的 x0及其到达条件

虽然它们都符合式(9)的要求,但它们的动态过程仿真结果却不同,其中 1,2,3为直达,而 4为绕达,如图 3所示.

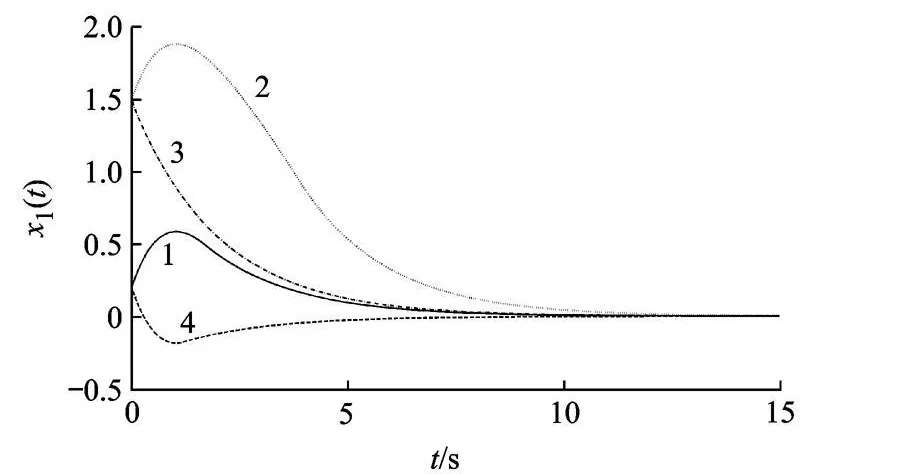
图3 滑模控制的直达和绕达现象

2.3 绕达原因的分析

滑模控制 u(式(7))是依据到达条件式(6)选择出来的.式(6)中,σ(x)＞0,σ(x)＜0,这意味着 x必不在 s上,因而 xj+1与 xj之间的比值就不应仍然保持为常数 Cij,应该是一个变量,例如表示为 dij.dij是随 x的变化而变化的,如示例系统中 1,2,3,4号 x0,其对应 d的值分别为 -4.5,-0.6,0.6,4.5,可见它们的值不是固定的 d=0.5,而是各不相同.而到达条件中的 σ·(x)的表达式却是σ·(x)=Cx·.不言而喻,该式等于把x的变化限制在了 s上,因为只有在 s上,xj+1与 xj之间的比值才是 Cij.所以传统滑模控制的到达条件的表述有误,致使滑模控制综合的结果错误,这是造成绕达现象的真正原因.

3 滑模控制的直达条件

滑模控制直达条件是选择开关型滑模控制的准则,按这种准则选择出来的控制,可使从 s邻域内 x0出发的相轨线直接到达其邻近的 s,相应的状态转移过程快速而无超调.

3.1 直达函数

定义 σd(x)=dx为直达函数,其中 d∈Rm×n是直达函数的状态变量之间的线性组合系数,每个组合系数表示为

其中,din=1.当 x的变化使得 d→C时,则有σd(x)→σ(x)=0.如果 d→C的过程中 d是单调变化的,则 σd(x)对于 s是直达的.

3.2 直达条件

容易证明,从 x0出发的相轨线到达 s的过程中,若不等式:

总是成立的(即存在改变的可能性),则该相轨线对于 s是直达的.对于式(3)所示系统,有 m=1,n=2,代入式(10)和式(11)分别得

直达条件是

其中,Δd＞0和 Δd＜0称为切换条件.它与传统滑模控制的切换函数中的 σ(x)＞0和 σ(x)＜0不等价.前者是 σd(x)绕相空间原点的正反方向旋转,后者是 σ(x)相对 σ(x)=0的平移.

4 直达滑模控制

直达滑模控制由指令运动模态及开关型直达滑模控制组成.

4.1 指令模态

指令模态 sc的形式多种多样,渐近稳定(或稳定)是它们共同的属性,等式 σc(x)=Cx=0是其中的一种.sc的动态品质完全取决于 C.

4.2 开关型直达滑模控制设计与仿真

满足不等式(11)的开关型控制 u,可将出发于 ΩNH的相轨线直接引导到 sc,并在 sc上趋向原点,称为开关型直达滑模控制 uDR.对式(3)所示系统,满足直达条件式(12)的控制是

将 1,2,3,4号 x0的相关参数代入式(13),分别计算 Δd=d-C及满足直达条件的控制 uDR,列于表2.

表 2 满足直达条件的控制uDR

表 2中数据表明,不同的 x0,uDR不同.如果选择开关型滑模控制:

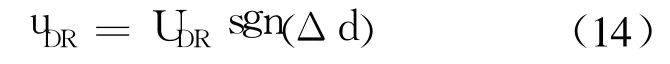
其中,UDR幅值满足条件

则 uDR可以使所有出发于以上 x0的相轨线直达sc.例如,对于式(3)所示系统取 UDR=3.2,则对于从 1,2,3,4号 x0出发的相轨线都可以直达 sc.

用式(13)检查到达条件开关型滑模控制的直达性.由于到达条件开关型滑模控制式(8)的U=0.5,而 4号 x0的 uDR＞3.15,4号相轨线不应该是直达的.而 1,2,3号 x0的 uDR都满足不等式-0.5＜uDR＜0.5,它们的相轨线当然都是直达的,这与相轨线的仿真结果一致.

把式(3)和式(14)合并在一起,对应1,2,3,4号 x0,x1(t)的仿真结果如图 4所示,可看出所有x1(t)均单向收敛.

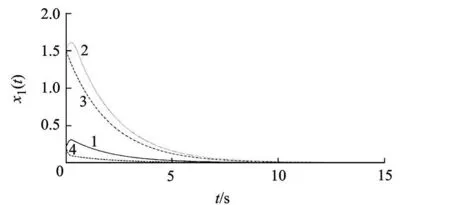
图4 直达滑模控制的动态过程

5 结束语

综上所述,导致滑模控制过程非单向收敛的原因是传统滑模控制到达条件表述不准确,致使对滑动模态的邻域界定有误.开关型直达滑模控制方法的核心组成是指令模态及开关型直达滑模控制,后者是通过指令模态的直达条件获取的.对于控制有界的直达滑模控制,需要界定满足直达条件的初始状态子空间.采用上述方法设计直达滑模控制系统,可保证滑模控制过程的单向收敛.

References)

[1]高为炳.非线性控制系统导论[M].北京:科学出版社,1991:544 GaoWeibing.Introduction to nonlinear control system[M].Beijing:Science Press,1991:544(in Chinese)

[2]Gao Weibing,Hung J C.Variable structure control of nonlinear system:a new approach[J].IEEE Transactions on Industrial electronics,1993,40(1):45-55

[3]Utkin V,Guldner J,Shi Jingxin.Sliding mode control in electromechanical systems[M].London:Taylor＆Francis Ltd,1999:36-39

[4]Gao Zhe,GuoWeian,Zheng Yan.Improved nonsingular term inal sliding mode controller design for high-order systems[C]//Proceedings of the 21st Annual International Conference on Chinese Control and Decision Conference.Piscataway:IEEE Press,2009:4874-4879

[5]Kuo K S,Shang Ruchen.Estimation of asymptotic stability region and sliding domain of uncertain variable structure systems with bounded controllers[J].Automatica,1996,32(5):797-800

[6]Choi H H,Chung M J.Estimation of the asymptotic stability region of uncertain systems with bounded sliding mode controllers[J].IEEE Transactions on Automatic Control,1994,39(11):2275-2278

[7]李文林.一种新的滑动模态到达条件[J].控制与决策,1995,10(4):322-326 Li Wenlin.A new reaching condition of sliding mode[J].Control and Decision,1995,10(4):322-326(in Chinese)

(编 辑:赵海容)

Direct reaching sliding mode control

Jiang Yuxian Zhou Yinqiang Zhao Xia

(School of Automation Science and Electrical Engineering,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)

Sliding mode control(SMC)system synthesized by traditional reaching condition can not grantee all phase trajectories from the neighborhood of the sliding mode to direct reach the nearby sliding mode branch.It will cause the state transition to be slow and overshooting which are not allowed in some engineering.In order to make the dynamic procedure of a SMC system unidirectional convergent,the direct-reaching SMC(DRSMC)was presented.By analyzing the shortcomings in the expression of traditional reaching condition,the definition of direct-reaching function and the establishment of direct-reaching condition were introduced.Direct-reaching condition(DRC)is the basis of using DRSMC to synthesizea SMC system.ADRSMC system is composed ofa command mode model and an on-off type DRSMC model.Different from the traditional reaching condition,the control which satisfies the DRC can guarantee all phase trajectories from the neighborhood of sliding mode to direct reach the nearby branch of the sliding mode and then go to zero state.Therefore the state transition process will be fast and monotonous.The DRSMC was applied to an example system and was simulated.The simulation resultaccords with the performance expectation of DRSMC.

sliding mode control;reaching condition;direct-reaching condition

TP 273

A

1001-5965(2011)02-0132-04

2009-11-27

姜玉宪(1937-),男,山东东阿人,教授,Jiangyuxian@buaa.edu.cn.