缝道参数对多段翼型气动性能的影响

秦绪国 刘沛清 屈秋林 彭国辉

(北京航空航天大学 航空科学与工程学院,北京 100191)

缝道参数对多段翼型气动性能的影响

秦绪国 刘沛清 屈秋林 彭国辉

(北京航空航天大学 航空科学与工程学院,北京 100191)

数值模拟研究缝道参数对着陆构型多段翼型气动性能的影响,采用有限体积法求解雷诺平均 N-S(Navier-Stokes)方程,湍流模型采用 S-A(Spalart-Allmaras)模型,给出了多段翼型升力系数与表面压力系数随各缝道参数的变化规律.计算结果表明:采用的计算模型可用于二维多段翼型的计算;缝道参数对多段翼型气动性能的影响显著,在各个缝道参数的变化范围内升力系数均存在最优值,适当的缝道参数可以抑制后翼上表面逆压梯度,消除后翼分离,并保持前翼尾迹不与后翼边界层相掺混,提高多段翼型的气动性能.

数值模拟;多段翼型;缝道参数;气动特性

多段翼型由前缘缝翼、主翼、后缘襟翼等组成.各段翼型形成的缝隙使流动变得非常复杂,其中包括边界层转捩、流动分离、尾迹流动的互相干扰等[1],各段翼形成的尾迹使后翼逆压梯度得到抑制,避免后翼分离,又与后翼边界层相互作用.因此多段翼型的缝道参数对流动影响很大,设计时必须考虑最优的缝隙参数[2-3].

国内外已有针对多段翼型缝道参数的实验研究[4]和数值研究[5].实验研究耗费成本高,模型尺寸小,缝道参数变换容易引起误差,多段翼型气动性能对缝道参数敏感,因此研究受限,未准确展现缝道参数的细微影响.采用数值模拟研究缝道参数的影响,能够研究缝道参数的细微影响,还能消除雷诺数效应.随着计算流体力学的发展,数值模拟已开始应用到多段翼型的模拟,并已有大量关于多段翼型计算的湍流模型的研究,文献[6]对近年来多段翼型的数值模拟进行总结,发现早期代数模型和经典 k-ε模型用于计算多段翼型分离绕流不够准确,而 S-A(Spalart-Allmaras)模型和SST k-ω(Shear Stress Transportk-ω)模型对多段翼型的气动特性、压力分布和空间速度分布等方面的模拟都比较准确.

本文数值研究缝道参数对多段翼型气动性能的影响规律,研究其流动机理,及其变化引起的流动特性.

1 数值方法

本文运用有限体积法求解非定常雷诺平均N-S(Navier-Stokes)方程,动量方程采用二阶迎风格式,粘性项采用二阶中心差分格式,速度与压力耦合求解,翼型表面采用无滑移边界条件.为使雷诺平均 N-S方程封闭,应用 S-A一方程湍流模型[7],该湍流模型从经验和量纲分析出发,由针对简单流动再逐渐补充发展,适用于带有层流流动的固壁湍流流动,引入了湍流运动粘性系数 ν～的输运方程,在多段翼型的计算方面取得了很好的结果.

2 结果与讨论

2.1 数值验证

为验证数值方法的正确性,首先与三段翼型30P30N的风洞实验结果[8]比较.实验马赫数Ma=0.2,雷诺数 Re∞=9×106.采用分区结构网格,数量为 18万.图 1为计算升力系数 Cl与实验对比,结果与实验吻合良好,在大迎角时缝翼偏差稍大,引起总的升力系数偏差稍大.图 2给出 α=19°时翼型表面压力系数 Cp与实验值吻合良好.

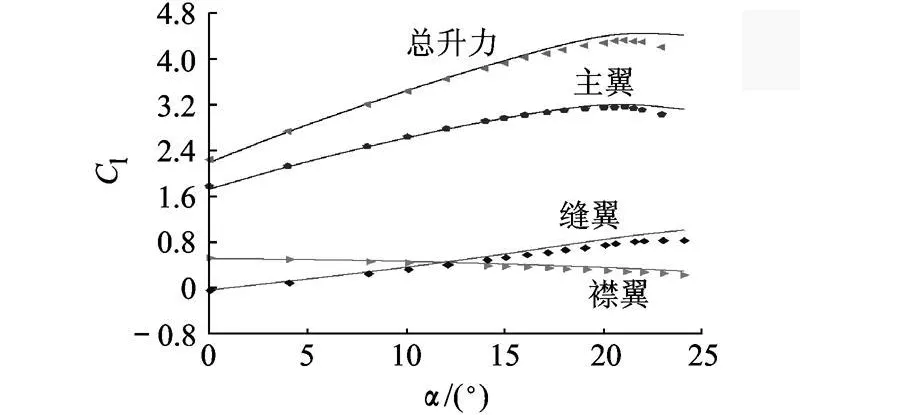
图1 计算升力系数与实验值对比

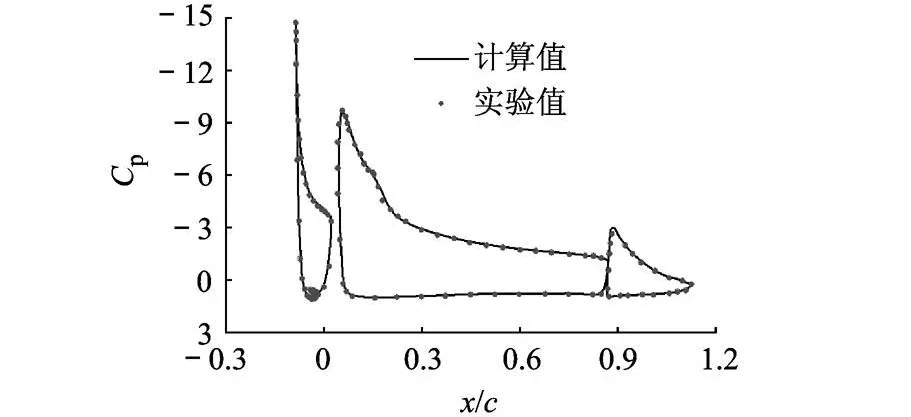
图2 计算压力系数分布与实验值对比

2.2 数值结果与分析

对某型客机着陆构型翼剖面的多段翼型气动性能进行数值模拟,研究缝道参数对其气动性能的影响.主要研究前缘缝翼与后缘襟翼的重叠量(Os,Of)、高度 (Gs,Gf)以及偏角 (δs,δf)6个参数.图 3为多段翼型变量示意图,规定重叠量的符号为:正值为重叠量的大小,负值为不存在重叠,其值为相离的距离.初始缝道参数为 Os=-0.02,Gs=0.0182,δs=33.18°,Of=0.013 76,Gf=0.008,δf=32.57°.固定迎角 α=18°,马赫数Ma=0.2,基于干净翼型弦长的雷诺数为 Re∞=5×106.图 4为计算区域翼型附近网格,采用分区结构网格,数量为 18.5万,壁面第一层网格厚度为10-5m.

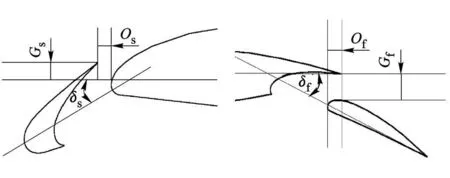
图3 缝道几何参数定义示意图

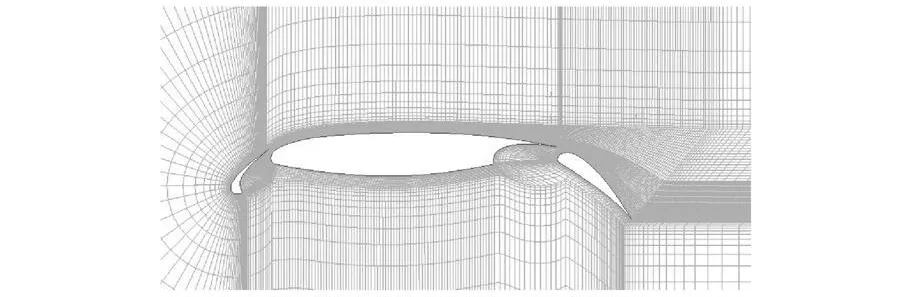
图4 计算区域网格分布示意图

2.2.1 前缘缝翼参数的影响

首先研究前缘缝翼重叠量 Os的影响.图 5为升力系数随 Os的变化,升力系数存在最大值,此时 Os=-0.006,Clmax=4.532.图 5b为翼型表面压力系数随 Os的变化,当 Os较小时,缝翼离主翼较远,缝翼尾迹对主翼上表面吸力峰值抑制作用较弱,主翼上表面逆压梯度太大,后缘出现了分离,随着缝翼逐渐靠近主翼,缝翼尾迹使主翼上表面逆压梯度减小,升力逐渐增加,达到最大值后,继续增大 Os,缝翼尾迹与主翼边界层掺混,使主翼上表面吸力损失较大,翼型升力迅速减小.

Gs对多段翼型升力系数的影响见图 6.升力系数随 Gs的变化存在最大值,此时 Gs=0.0182,Clmax=4.532.图 6b为翼型表面压力系数随 Gs的变化规律.Gs通过影响缝道宽度影响主翼前缘吸力峰值,适当减小 Gs可以使缝翼尾迹对主翼上表面气流影响增大,主翼段逆压梯度减小,延缓主翼气流分离的出现.达到最大升力系数后继续减小Gs,缝翼尾迹对主翼前缘吸力峰的抑制作用更强,主翼段上翼面吸力严重衰减,翼型升力系数降低.

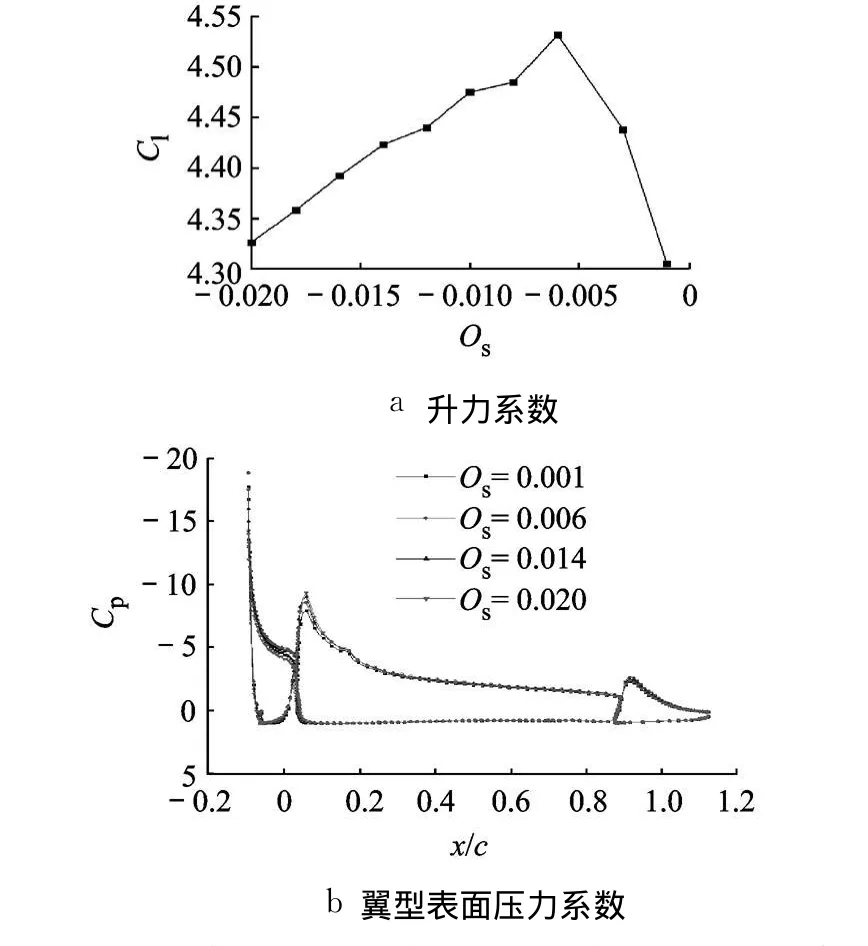
图5 前缘缝翼缝隙重叠量对多段翼型的影响

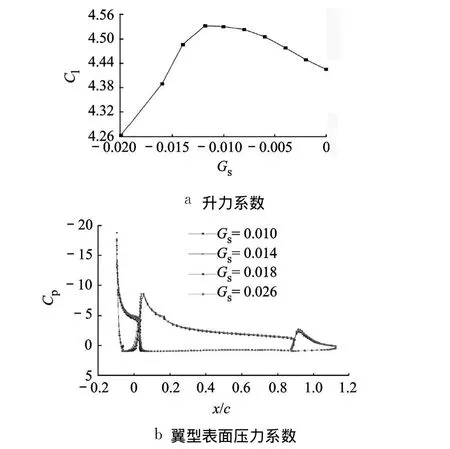
图6 前缘缝翼缝隙高度对多段翼型的影响

δs对升力系数的影响见图 7,升力系数随 δs的变化存在最大值,此时 δs=33.18°,Clmax=4.532.δs的影响主要体现在对缝翼尾迹厚度的控制,适当的 δs可以改善缝翼尾迹的厚度,减弱尾迹对主翼前缘吸力峰值的抑制作用,提高主翼吸力.图7b为 δs对翼型表面压力系数的影响,缝翼在小偏角时,前缘缝翼上的最大吸力峰值较大,但缝翼尾迹较厚,主翼吸力峰值较小,随着 δs的增大,缝翼尾迹流动变薄,主翼上表面吸力增加,升力系数增大,达到最大值后,继续增大偏角 δs,缝翼尾迹流动变厚,主翼上表面吸力降低,升力系数降低.

2.2.2 后缘襟翼缝道参数的影响

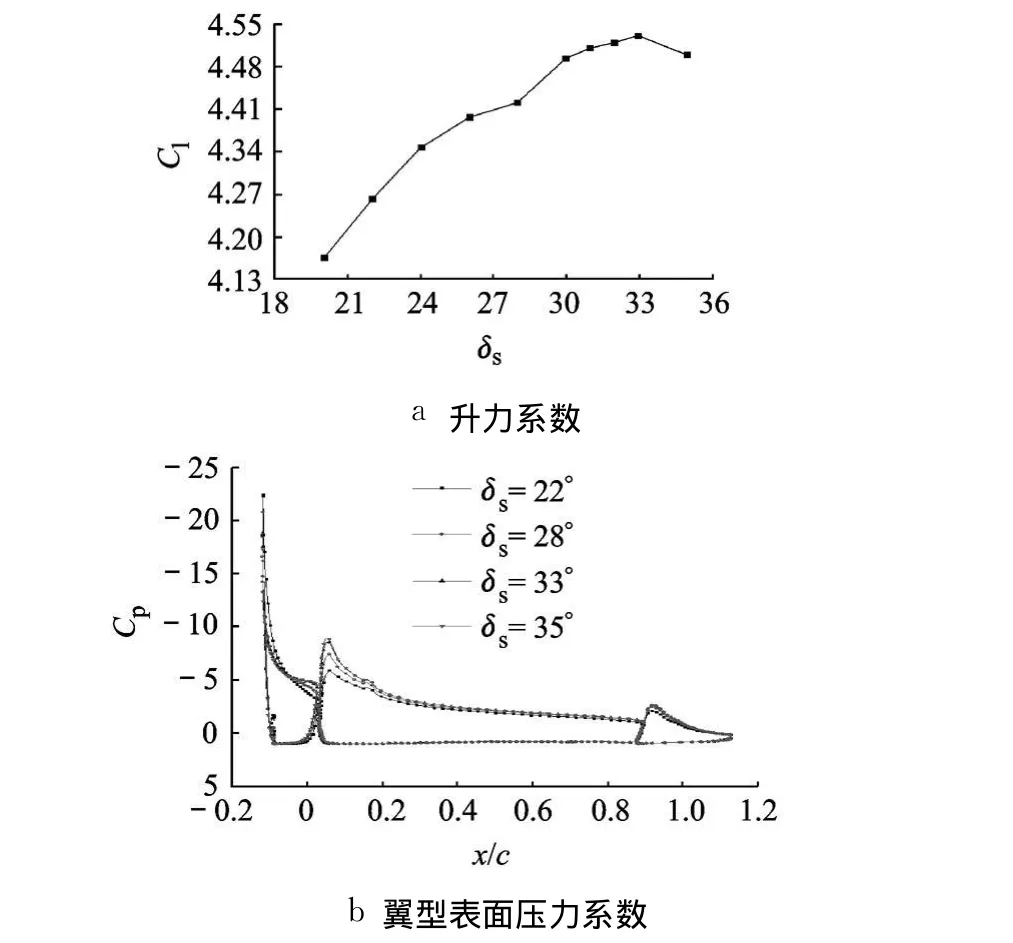
图7 前缘缝翼偏角对多段翼型的影响

研究后缘襟翼缝道参数的影响时,缝翼缝道参数为 2.2.1节中的最优值不变,即 Os=-0.006,Gs=0.0182,δs=33.18°.图 8为 Gf对升力系数的影响,Gf=0.015时达到最大值 Clmax=4.637.图 8b为 Gf对翼型表面压力系数的影响,Gf＜0.015时,随着 Gf的增大,主翼段尾迹对襟翼吸力峰的抑制作用减弱,襟翼的倾卸作用与环量均增强,使多段翼型总的升力增加;Gf＞0.015后,主翼尾迹对襟翼上表面吸力峰的抑制作用进一步减弱,逆压梯度增加,继续增大 Gf,襟翼开始出现分离,如图 9所示,襟翼对主翼的环量诱导作用迅速减小,升力系数也迅速降低.

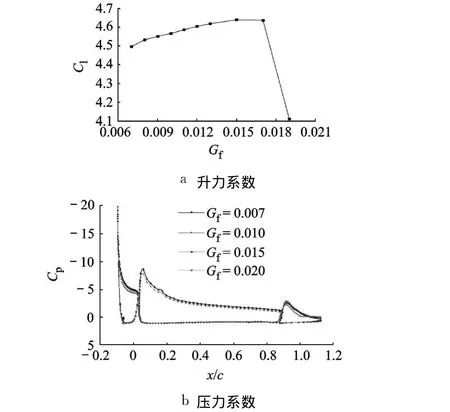
图8 后缘襟翼缝隙高度对多段翼型的影响

Of对多段翼型升力系数的影响如图 10所示,Of=0.02时,达最大值 Clmax=4.65.图 10b为 Of对翼型表面压力系数的影响,Of＞0.02时,Of对表面压力系数的影响较为微弱,升力系数变化不大,后缘襟翼均保持附着流动;Of＜0.02后,襟翼距离主翼较远,主翼尾迹对襟翼上表面逆压梯度的抑制作用减弱,襟翼继续远离主翼,襟翼上表面流动出现分离,襟翼对主翼的环量诱导作用迅速减少,翼型升力系数也迅速降低.

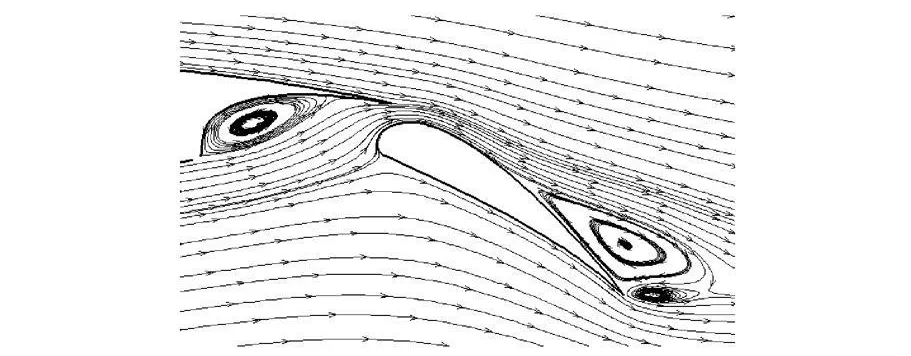
图9 多段翼型空间流线图,Gf=0.02

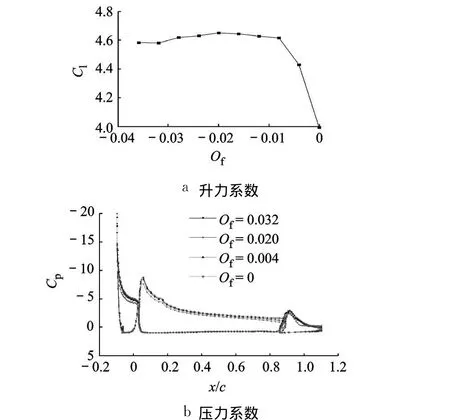
图10 后缘襟翼重叠量对多段翼型的影响

δf对升力系数的影响如图 11所示,δf=40°时,达到最大值 Clmax=4.793.

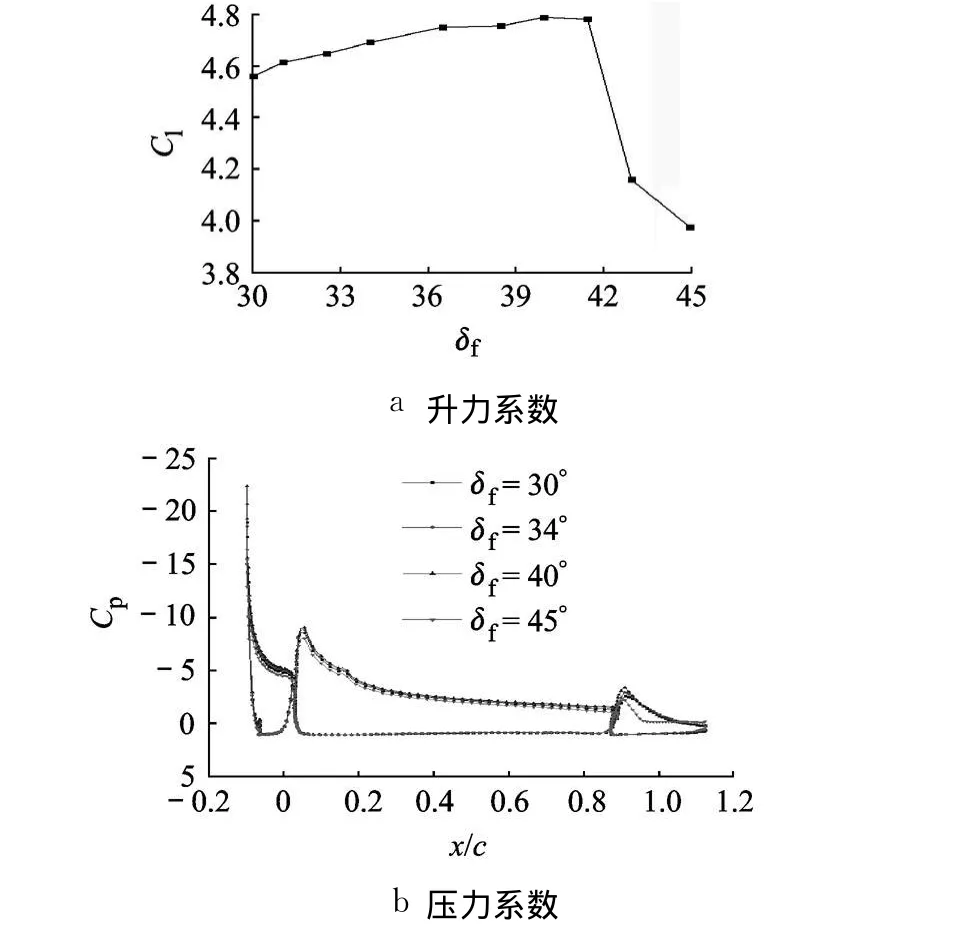
图11 后缘襟翼偏角对多段翼型的影响

图11b为 δf对翼型表面压力系数的影响,δf＜40°时,δf增大,襟翼环量增加 ,诱导主翼环量增大,主翼下表面后缘气流流速增加,主翼上表面逆压梯度减小,使得主翼上表面吸力增加;δf＞40°时,主翼尾迹对襟翼流动的控制减弱,导致襟翼上表面出现分离,襟翼对主翼的环量诱导作用迅速减弱,主翼上表面吸力下降,因此翼型升力系数迅速减小.

3 结 论

本文利用数值模拟研究缝道参数对多段翼型气动性能的影响,结果表明缝道参数对多段翼型气动性能的影响是非常显著的,缝道参数均存在最优值.

优化的缝道参数能明显改善多段翼型气动性能,使多段翼型环量增大,抑制后翼吸力峰值,避免产生分离,并避免前翼尾迹与后翼边界层掺混,提高升力系数.

References)

[1]朱自强,陈迎春,吴宗成,等.高升力系统外形的数值模拟计算[J].航空学报,2005,16(3):257-262 Zhu Ziqiang,Chen Y ingchun,Wu Zongcheng,et al.Numerical simulation of high liftsystem configuration[J].Acta Aeronautica et Astronautica Sinica,2005,16(3):257-262(in Chinese)

[2]Meredith P T.Viscous phenomena affecting high lift systems and suggestions for futureCFD development[C]//AGARDCP 315.London:[s.n.],1993:19-1-19-8

[3]Smith A M O.High lift aerodynam ics[J].Journal of Aircraft,1975,12(6):501-530

[4]Thomas F O,Nelson R C,Liu X.Experimental investigation of the confluent boundary layer of a high-lift system[J].AIAA Journal,2000,38(6):978-988

[5]Balaji R,Bramkamp F,Hesse M.Effect of flap and slat riggings on 2-D high-lift aerodynamics[J].Journal of Aircraft,2006,43(5):1259-1271

[6]Rumsey C L,Ying S X.Prediction of high lift:review of present CFD capability[J].Progress in Aerospace Science,2002,38(2):145-180

[7]Spalart P R,A llmaras SR.A one-equation turbulence transport model for aerodynam ic Flows[R].AIAA 92-0439,1992

[8]Chin V,Peters DW,Spaid FW,et al.Flow fieldmeasurementsabout amulti-elementairfoil at high reynolds Numbers[R].AIAA 93-3137,1993

(编 辑 :李 晶)

Influence of gap parameters on aerodynamics of multi-element airfoil

Qin Xuguo Liu Peiqing Qu Qiulin Peng Guohui

(School of Aeronautic Science and Engineering,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)

The effect of flap and slat riggings on the multi-element airfoil was investigated numerically.The compressible Navier-Stokes equations were solved by the finite-volume method.Spalart-Allmaras(S-A)turbulencemodel was used.The effects of flap and slat riggings on lift coefficients and pressure coefficients were provided.The validation of computation agreed well with the experimental results.The computations on the effect of flap and slat riggings shows that lift coefficient has an optimum with every design parameter.With proper flap and slat riggings,the adverse pressure gradient and the separation on the backward wing section could be suppressed,and the wake from forward wing section does not mix with the boundary layer of backward wing section.So the performance of the airfoil can be improved.

numerical simulation;multi-elementairfoil;gap parameter;aerodynamic character

V 211.4

A

1001-5965(2011)02-0193-04

2009-12-10

国家 973重点基础研究发展计划(2009CB72400101);“凡舟”青年科研基金资助项目(20090504)

秦绪国(1982-),男,山东青岛人,博士生,qinxuguo@ase.buaa.edu.cn.