飞机拦停网强度及拦停系统性能评估的数值方法

邓 瑛 闫晓军 张 辉

(北京航空航天大学 能源与动力工程学院,北京 100191)

飞机拦停网强度及拦停系统性能评估的数值方法

邓 瑛 闫晓军 张 辉

(北京航空航天大学 能源与动力工程学院,北京 100191)

为了评估飞行器拦停系统性能以及拦停网强度裕度,采用非线性动力学有限元方法模拟了飞机拦停系统的工作过程,考虑了飞机外形、飞机和捕获装置间的相互作用、捕获装置重量、材料性能等因素对拦停过程的影响,解决了建立有限元模型、添加边界条件以及计算中非线性因素多,收敛困难等关键技术问题,获得了捕获装置在工作过程中应力的演化规律,完成了捕获装置拦停性能验证以及拦停系统结构强度、裕度评估.通过将理论分析结果与试验数据对比后表明:该方法可用于评估拦停系统拦停效率并预测捕获系统的强度储备,为今后设计拦停系统提供有效的分析方法.

飞行器拦阻装置;数值模拟;冲击;强度

飞机拦停系统的使用可追溯到 20世纪 50年代,主要用于对故障飞机进行紧急制动,将事故可能造成的损失降至最低,是机场的重要地面设备之一[1].

为了更为有效地保护飞行器,人们不断地推出新型的拦停系统.一般而言,拦停系统的设计工作可分为以下几个方面:①根据拦停对象、飞行跑道的几何特征确定的捕获系统的大致尺寸,对捕获系统的设计要求为能够捕获不同外形的飞机,并且具备足够的强度;②根据拦停对象特征提供相应的拦停控制规律,该规律反映拦停过程中不同时刻所对应的拦阻力,在此基础上完成捕获系统具体结构设计;③选择适当的制动器、控制器.

拦停控制规律是整个拦停系统的核心之一,直接决定了拦停系统的性能:拦停距离和最大拦停加速度.其中拦停距离定义为从拦阻网所在地到飞机停止位置间的距离.目前,拦停控制规律的设计过程大致分为两步:①针对整个系统建立数学模型,该模型的实质是一系列的二阶微分方程,以飞机的触网速度、重量为初始条件,以拦停距离、拦停最大加速度为控制参量求解方程,从中选定满足要求的拦停控制规律及参数;②根据拦停控制规律估算出作用在拦阻网、刹车带上的载荷,并根据载荷大小最终完成捕获系统、刹车带的结构设计.

通过以上分析可以看出,现有的设计方法[2]存在一定的不足:在设计拦停控制规律时所建立的数学模型将飞机简化为一个质量块,拦阻网、刹车带仅作为力传递介质,作用在拦阻网、刹车带上的载荷则根据拦停控制规律获得.在该数学模型中,飞机的几何特征,网体、刹车带材料性能、几何特征、重量等因素以及飞机和网体间的相互作用对拦停过程的影响几乎没有得到考虑.这种简化所导致的不利因素为:①难以考虑拦阻时的冲击对捕获系统强度的影响,为保证捕获系统具备足够的强度,往往需要根据经验选取较大的安全系数;②不能考虑飞机几何特征对拦停过程的影响;③不能评估所设计的拦停控制规律在真实情况下拦阻飞机的效果.

综上所述,传统的设计方法存在不足,尤其是其难以验证拦停控制规律并进行捕获系统的强度分析,针对以上缺陷,本文开展了相关的研究.

1 分析过程及思路

由于拦停过程复杂,研究中存在较多的难点:首先,拦阻系统结构复杂,包含捕获装置、刹车带以及制动装置,如何对系统进行简化,建立合理的有限元分析模型是研究中首先遇到的难题;其次,如何在有限元模型中添加合理的边界条件也是研究中的难点;最后,拦停过程中加载率高,存在着接触、大变形等诸多非线性因素,因此还需采用适当的措施保证计算的收敛性.本文在研究中选用有限元软件 PAM-Shock作为求解器,具体分析过程分为 3步:①利用有限元软件对拦停过程进行模拟;②对比实验数据及计算结果,验证计算方法的可行性与计算精度.③对验证后的计算模型进行拦停控制规律验证并对捕获系统强度进行评估、验证拦停控制规律.

1.1 系统简化及建模

本文的研究目的为验证拦停控制规律以及捕获系统强度,因此,研究对真实拦停系统(如图 1所示)进行简化建立的有限元模型,如图 2、图 3所示.其中图 2为整个有限元模型;图 3为拦阻网网体细节.

建立有限元模型的难点在于如何对拦停系统进行合理的简化.研究中根据拦停系统的工作过程及结构特征进行简化:通常,拦停系统由拦阻网、刹车带以及制动器等部件构成,其中,拦阻网用于捕获飞机;刹车带用于连接拦阻网与制动装置,其一端与拦阻网连接,另一端缠绕在绞盘上,制动装置与绞盘连接.但制动装置并非研究对象,因此没有建立有限元模型.由于在有限元模型中省略了绞盘及制动装置,刹车带模型将被展开,放置在飞机两侧并平行于飞机运动的方向.建模时保证刹车带具备足够的长度,如图 2所示,在该图中仅显示部分刹车带模型.

研究所建立的有限元模型省略了制动装置,因此如何添加边界条件,特别是拦停控制力边界条件将是研究中面临的另一个难点.

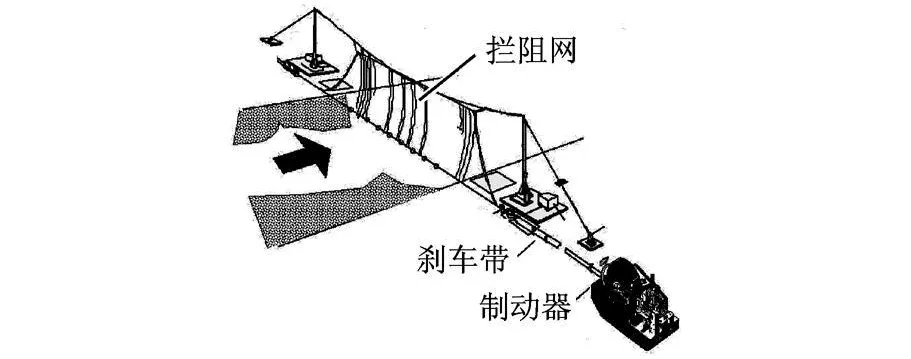
图1 拦阻系统组成示意图

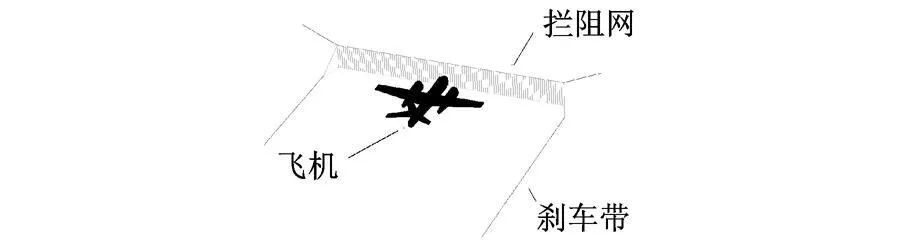
图2 有限元模型

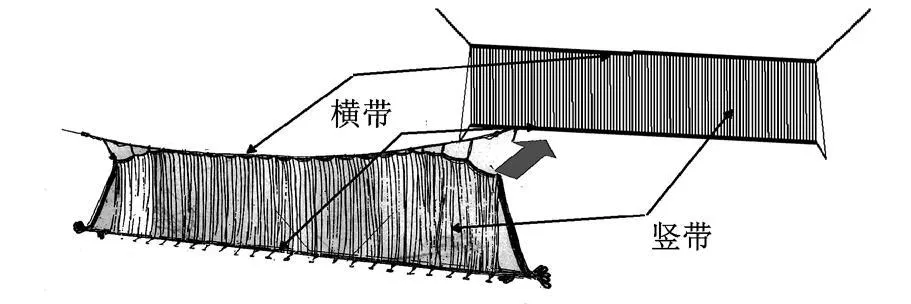
图3 网体及其有限元模型

1.2 边界条件的施加

在建立有限元模型后还需要添加合理的边界条件,如拦停控制规律.拦停控制规律是拦停系统的重要控制参数,对于特定拦停系统,所需拦截飞机的重量、速度等拦停参数确定后即可确定相应的拦停控制规律,该规律可以表示为时间的函数,如图 4所示.本文中将采用如下步骤把拦停控制规律添加到有限元模型中.

1)在拦停过程中,制动器根据拦停控制规律对刹车带施加的拦停控制力 F可表示为拦停时间 t的函数,该函数可转换为刹车带伸长量 L同F的函数,如图 5所示.其中 L的含义如图 6所示.通常情况下,拦停系统控制器记录 F-t的数据,然而在拦停过程中刹车带由于力作用将会发生变形.为了考虑刹车带变形对拦停过程的影响,故选用 L-F函数关系作为边界条件.该函数关系可根据拦停距离、拦停时间与拦停控制力间函数关系转换后得到,在转换过程中耦合了飞机的运动方程和刹车带材料的本构方程.

图4 拦停力随时间变化规律

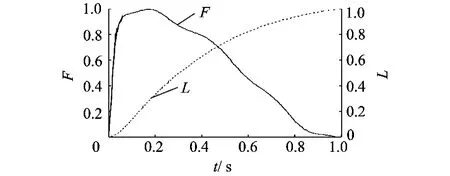
图5 拦停力、刹车带伸长量随时间变化规律

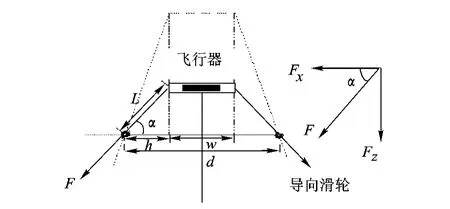
图6 F的分解

2)将作用在刹车带上的拦停力将按照图 6所示分解为两个分量:Fx,Fz.

3)Fx,Fz作为边界条件被添加到刹车带特定单元的节点上.通过对拦停过程分析可知,刹车带被拖离绞盘后都将通过一个导向滑轮,如图 6所示.因此,当某一节点在特定时刻到达导向滑轮处时,该节点上即被施加对应时刻的拦停控制力.而与此同时,刹车带其余节点上拦停力为 0,作用在该节点上的拦停控制力将被保持一段时间,当下一个节点运动到导向滑轮处后作用于上一个节点的拦停力被撤销,相应的拦停控制力也随之转移到下一个节点上.

当边界条件施加完毕后即可对拦停过程进行模拟,但是在拦停过程中还存在诸多非线性因素,因此需要采取相应措施保证计算收敛.

1.3 非线性因素及收敛条件

对拦停过程的研究面临着大量的非线性因素,例如:材料性能、接触问题、大变形、高应变率等.因此,如何保证计算收敛性是研究中的另一个难点,研究中本文采用了以下一系列的措施.

1)飞机从被捕获并在拦阻网体的作用下最终停止运动,网体和机体间的相互作用可看作刚性体和柔性体的接触问题,并且在捕获瞬间,其相对运动速度较高.为了保证网体能顺利捕获飞机,对拦阻网体施加几对作用力,这些力很小并且作用时间被限制在网体对飞机的捕获过程内,力方向则处于拦阻网体平面内.

2)由于较高的加载率而造成的高应变率,研究中采用了能够考虑应变率的 Johnson-Cook模型描述飞机结构在拦停过程中的力学行为,如式(1)所示,研究发现,如果采用其他本构模型,在分析过程中将出现收敛困难的问题.

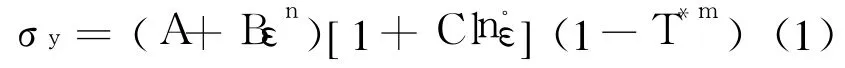
其中,T*为等效温度,A,B,C,n,m为常数,分别为:A=265MPa,B=426MPa,n=0.34,C=0.015,m=1.0,T*m=775K[3].网体、刹车带材料相同,材料性能如图 7所示.

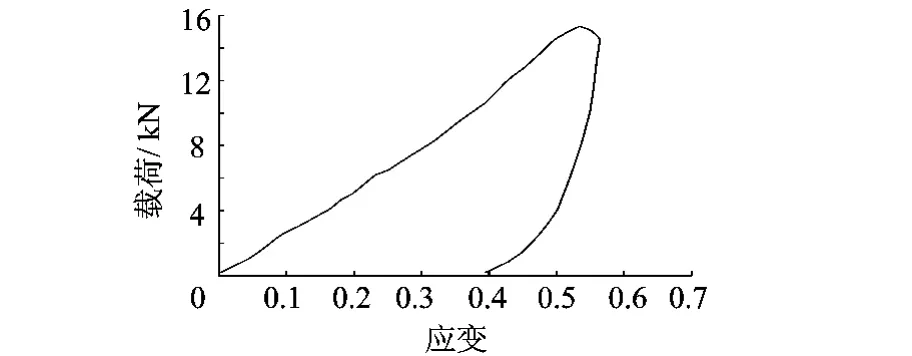
图7 拦阻网体材料单调拉伸实验数据

2 结果及分析

研究中,所需拦停的飞机重 14 t,触网速度为185km/h,计算中使用的拦停力控制规律由控制器提供,变化规律如图 8所示.

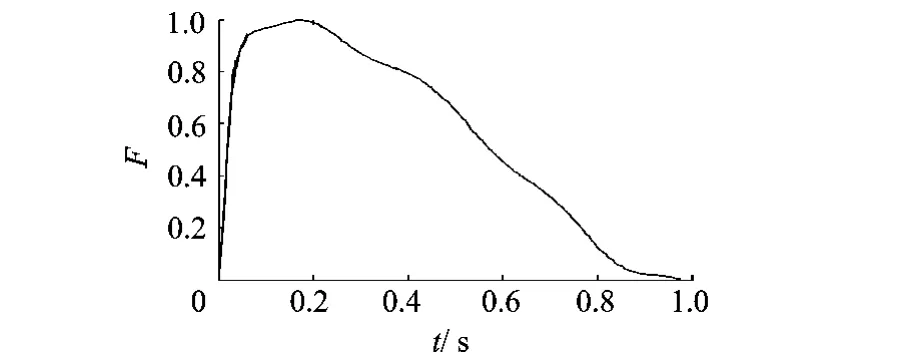
图8 拦停控制力随时间的变化规律

拦停系统设计过程中的两个重要指标,拦停距离、最大拦停加速度的演化规律如图 9、图 10所示.计算结果和实验数据的对比如表 1所示,可以看出,实验数据和计算结果吻合得很好.

表 1 实验数据与计算结果对比

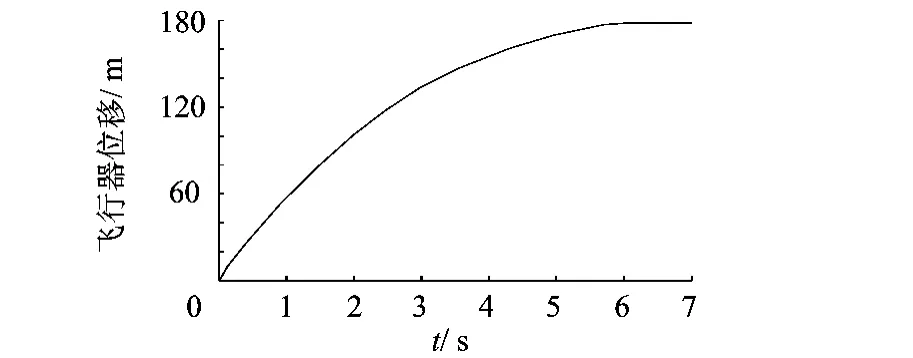
图9 计算得到的拦停时间/拦停距离曲线

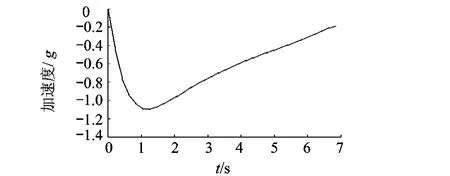
图10 计算得到加速度/时间曲线

为了评估拦阻网、机体在拦停过程中的强度裕度,给出了最大加速度时刻所对应的机体、拦阻网体的应力分布,如图 11所示.危险点应力随时间的演化规律如图 12所示.其中,横带危险点最大载荷为 8.64 t,远低于该带的强度(90 t).竖带的危险点载荷演化规律也如图 12所示,其最大值为 4.48 t,小于竖带的拉伸强度(5 t),但其强度储备不充足.

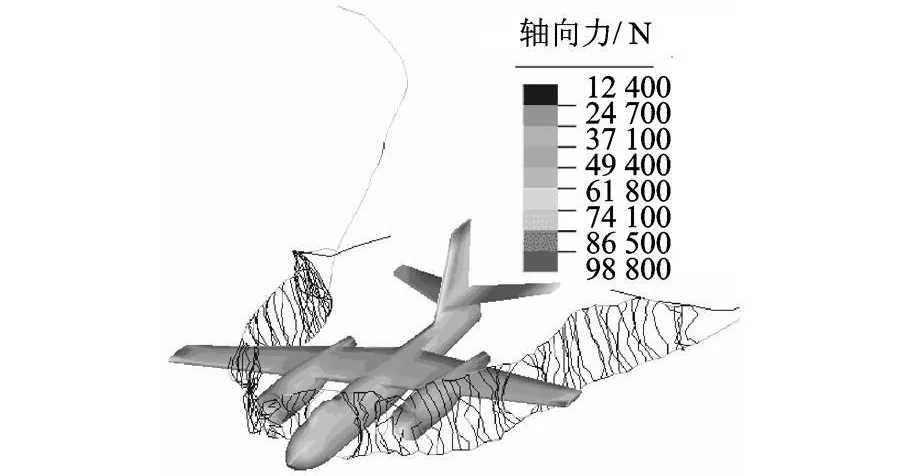
图11 拦阻网及机体应力分布云图

图12 拦阻网体危险点应力随时间变化规律

该方法的另一个优点为可以很方便地分析飞机在拦停过程中的应力演化规律,其应力云图如图 13所示,根据机体应力水平可以对拦停过程对机体造成的损伤进行评估,计算得到拦停对飞机产生的应力远低于机体的材料强度.因此,可认为飞机机体结构在拦停过程中是安全的.

图13 机体正应力分布云图

3 结 论

目前,针对飞机拦停系统的设计方法未能考虑飞机的几何特征,网体、刹车带材料性能、几何特征、重量等因素以及飞机和网体间的相互作用对拦停过程的影响,难以预测捕获系统结构强度裕度,评估所确定的拦停控制规律的拦停效果,因此,该方法不能满足未来捕获系统强度设计的要求.

对于拦停系统设计中存在的不足,本文采用了有限元方法研究了拦停过程,提出了建立有限元模型的方法,解决了在有限元模型中添加边界条件困难及数值计算过程中非线性因素造成的收敛困难问题.计算结果表明该方法可对飞机拦停过程进行模拟,可获得捕获系统应力分布及演化规律,从而可对拦阻网体的结构强度进行评估.此外,该方法还可获得拦阻过程中飞机加速度变化规律及运动规律,可用于已有拦停控制规律的验证.

References)

[1]Hartzer R B.From sandbags to MAAS:aircraft arresting systems[J].Air Force Civil Engineer Magazine,1993,7:1-3

[2]Hsin CC.Arresting landing studies for STOL aircraft[J].Journal of Aircraft,1974,11(3):159-165

[3]Edit group of world aircraft manual.World aircraft manual[M].China:Aviation Industry Press,2001

[4]Hsin CC.Arrested landing studies for STOL aircraft[C]//Hsin CC.Annual Meeting and Technical Display,Washington D C:Virginia University,Charlottesville,1973:1-10

[5]李启明,冯蕴雯,于立明.飞机拦阻着陆动力学分析与仿真[J].计算机仿真,2010,27(1):27-31 LiQiming,Feng Yunwen,Yu Liming.Kinetics Analysis and simulation of aircraft arrested shore-landing[J].Computer Simulation,2010,27(1):27-31(in Chinese)

[6]张明晖,袁理,洪冠新.航空母舰液压拦阻系统拦阻力建模与仿真[J].北京航空航天大学学报,2010,36(1):100-103 Zhang Minghui,Yuan Li,Hong Guanxin.Aircraft carrier hydraulic arresting gear arresting force modeling and simulation[J].Journal of Beijing University of Aeronautics and Astronautics,2010,36(1):100-103(in Chinese)

(编 辑 :张 嵘)

Net barrier strength and perform ance evaluation of AAS by FE method

Deng Ying Yan Xiaojun Zhang Hui

(School of Jet Propulsion,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)

The performance of aircraft arresting system(AAS)and strength of net barrier was evaluated by means of nonlinear finite element(FE),considering contact,net mass and material properties.Key problems,such as FEmodel,boundary condition and numerical convergence caused by compl exnonlinear system,were solved.The simulation results provide stress distribution of AAS to evaluate strength margin of the net barrier.It is worth well of pointing out that the method can also be used to check effectiveness of controller's method.The results also show that this method could describe arresting processes closely to actual state.Consequently,the procedures can be effective in an AAS design.

arresting device;simulation;impact;strength

V 351.392

A

1001-5965(2011)02-0171-04

2009-12-24

全国优秀博士学位论文作者专项资金资助项目(200351);教育部“新世纪优秀人才支持计划(NCET-06-0178);北京航空航天大学博士创新基金

邓 瑛(1980-),男,云南昭阳人,博士生,YingDeng@sjp.buaa.edu.cn.