关于镇墩稳定计算的探讨

谭永华 许长红 昌彩霞

（中国水电顾问集团中南勘测设计研究院 长沙市 410014）

镇墩是重要的水工建筑物，镇墩的安全与否直接关系到泵站或电站的安全，因此，必须重视镇墩的作用，务必使镇墩保持稳定。镇墩本身是比较简单的建筑物，但由于埋入其内的压力钢管的布置可能比较复杂，而且由于镇墩所处的地质条件往往变化较大，在诸多不利因素的组合下，可能会使得镇墩的受力非常复杂。

镇墩的稳定计算主要包括抗滑移、抗倾覆、地基承载力和沉降计算四个方面。经验表明，起控制作用的因素经常是基底应力，而且往往不是由最大基底应力控制，而是由最小基底应力控制。目前国内没有关于镇墩设计的专用规范，故在工程设计中只能参考 《水电站厂房设计规范》、《混凝土重力坝设计规范》、《泵站设计规范》等规范的规定进行设计。

1 力矩的分解

在实际设计中，由镇墩上、下游钢管传给镇墩的力矩可能与镇墩主轴不正交或平行，使得镇墩的抗倾覆和基底应力计算复杂化。笔者认为，将此类力矩分解可以使计算简化。举例如图1所示：

以AB为转动轴进行抗倾覆计算，作用的外力矩有M，M与X轴的夹角为α。计算时，倾覆力矩应为

可以采用等效替代的方法进行分析。可以用一个集中力F和力臂a，使M=F×a，且集中力F产生的力矩方向与M相同，同时，在截面中心点O处作用一个与集中力F大小相等方向相反的集中力F′，如此，则F和F′的共同作用即等效于 M。而F则可以在X轴和Y轴上分解为Fx和Fy，其中Fx=F×cos（α），Fy=F×sin（α）。显然，此时倾覆力矩应为：

图1 力矩M示意图

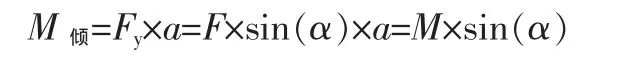
同理，在基底应力计算中，相对于X轴的转动力矩应为：

相对于Y轴的转动力矩应为：

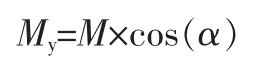
以角点B为例，其基底应力值为

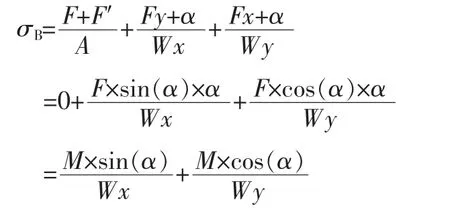
只要等效替代的F与α满足M=F×α，上式恒成立。故基底应力计算时也可以对力矩进行分解。

2 抗倾覆稳定计算时应避免的错误

根据 《泵站设计规范》（GB/T50265-97）附录C.0.2.3条的规定，镇墩抗倾覆稳定应按下式计算：

式中 K0——抗倾覆稳定安全系数；

[K0]——允许的抗倾覆稳定安全系数；

y0——作用在镇墩上的垂直合力的作用点距倾覆原点的距离；

x0——作用在镇墩上的水平合力的作用点距倾覆原点的距离；

Σy——荷载在y轴方向的投影之和；

Σx——荷载在x轴方向的投影之和。

对上式进行展开即：

在图2中，镇墩自重为G，高度为h，宽度为b，点B处作用一外力F，F恰好穿过角点C。以C点为转动点。将F分解为Fx和Fy，如下图3所示。

图2 作用力F示意图

图3 作用力F分解示意图

按式（1）计算抗倾覆稳定安全系数为：

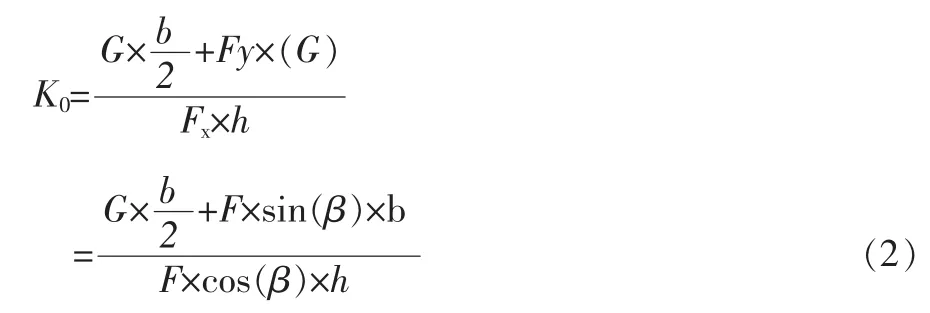
在计算镇墩抗倾覆稳定时，应避免以下错误计算，即

式（3）的错误在于没有认清式（1）的实质是抗倾覆力矩与倾覆力矩之比，称为抗倾覆稳定系数。F通过C点，力矩MF为0，是不错的，但并不等于F产生的抗倾覆力矩为0，也不等于F产生的倾覆力矩为0。F产生的抗倾覆力矩为F×sin（β）×b，产生的倾覆力矩为F×cos（β）×h。所以式（3）计算所得的K0不是抗倾覆稳定系数，式（3）是错误的。在设计镇墩时应注意避免类似错误的发生。

《混凝土重力坝设计规范》（SL319-2005）和《砌石坝设计规范》（SL25-2006）在稳定计算中均已取消抗倾覆稳定计算，因为只要坝基应力满足规范控制要求，即可满足抗倾覆稳定要求，不必进行抗倾覆稳定复核，笔者认为只要规范对镇墩基底应力的控制要求参照 《混凝土重力坝设计规范》和《砌石坝设计规范》制定，在镇墩设计时可取消抗倾覆稳定复核，减少设计工作量。

3 如何确定底截面的形心主轴

形心主轴对于计算基底应力是至关重要的。所有的外力矩都必须是相对于形心主轴而言的，否则便会得出错误的计算结果。

对于规则的镇墩底截面而言，形心主轴是很容易确定的，但在实际设计中，完全可能因为布置的需要而将镇墩的底截面设计成较不规则甚至很不规则的形状，那么，对于这种不规则的底截面应该如何确定其形心主轴呢？常规的做法是先求出截面形心，再通过积分方法求出底截面相对于选定的坐表轴的惯性积，若求出的惯性积不为0，再旋转一下坐标轴后再积分求惯性积，直到达到满意的精度为止。事实上，这是理论方法，对于手工计算而言是不可能的，既浪费时间又得不出结果。但是，在AutoCAD上却可以快速而准确地找到形心主轴，方法很简单。首先，将底截面做成一个面域，然后通过查询“质量特性”功能就可以轻松地找到截面形心点，再将坐标原点移至找到的截面形心点上，通过反复地微调旋转面域，当最后惯性积趋近于0时，所得到的坐标轴即是要找的底截面的形心轴。

4 镇墩计算时如何简化各力的计算

在镇墩稳定计算中，由于由压力钢管传至镇墩的分力数量多，且一些力方向多变，工况组合复杂，因此，计算时很容易混淆出错。其实，可以利用矩阵来解决这个问题。数学计算软件MathCAD中，可以自由定义计算式和矩阵，可以将众多分力赋为矩阵的变量，对各矩阵根据需要进行叠加运算。矩阵法的优点很明显，数据容量大，计算明了，不易出错；但矩阵法也有不足之处，在于物理概念不甚清晰，同是了为追求数据的“整齐”而忽略了压力钢管传至镇墩的力的精确性，会带来一定的误差。不过，总体而言，矩阵法误差相对较小，是可以接受的。

5 台阶形镇墩的处理方法

通常镇墩底面都是平底，但也有相当部分镇墩底面是台阶状，这就带来了一个问题，计算基底应力时这些台阶如何处理？在常规计算中，工程设计人员仍然视台阶底为平底。事实上，这样做是有误差的。在外力和外力矩作用下，镇墩底部的地基受力，发生变形，与台阶相接触的地基与镇墩一起协调变形，与平底是有区别的。如果想要精确地得知地基的应力分布，靠目前的刚体极限平衡法是不行的，只有将各分力计算清楚后，按有限元法建立计算模型进行计算。应该讲，有限元建模虽然精度较高，但费时费力，远不如刚体极限平衡法快捷，故在日常设计中刚体极限平衡法虽有一定的误差，但设计经验丰富，安全余度可控，应用相对较多，只有对很复杂又很重要的镇墩才采取有限元法进行复核计算。

6 对于抗倾覆不易满足要求的情况的处理

在实际设计中，也有那种地基较低，压力钢管较高且伴有平面弯段，致使镇墩较高，因而抗倾覆计算时较难满足规范要求的情况。对于此种情况，盲目加大、加高镇墩是不经济的，可以采用摊大镇墩底截面、加厚压力钢管上覆厚度、尽可能浅挖、基底置换的办法来达到抗倾覆稳定的目的；同时，也可以将镇墩四周回填碴土并压实，利用土压力的有效作用。需要说明的是，土压力也不是任何情况下都有利；同时，土压力也不方便量化取值，难以精确计算；因此，实际设计时多将有益土压力作为安全储备，而将有害土压力按最不利情况计其影响。

7 结语

镇墩的受力是复杂的，而其布置是多变的，在工程设计中尚有许多问题需要进一步探讨。

1 SL266-2001.水电站厂房设计规范[S].

2 SL319-2005.混凝土重力坝设计规范[S].

3 GB/T50265—97.泵站设计规范[S].

4 SL379-2007.水工挡土墙设计规范[S].