基于小波包变换的FED驱动电路故障诊断

2011-03-15林雪芬郭太良姚剑敏林志贤

电视技术 2011年11期

林雪芬，郭太良，姚剑敏，林志贤，徐胜

（福州大学物理与信息工程学院，福建福州 350002）

0 引言

由于模拟电路故障诊断过程庞大、繁琐，元件容差带来的不确定误差以及众多非线性因素等[1]容易影响故障诊断结果。采用一般的故障诊断方法存在一定的局限性，如基于冯·诺依曼计算机的故障字典法只能检测单硬故障，K故障法仅适用于线性电路，且受网络拓扑的限制。基于神经网络的故障诊断法克服了这些问题。

目前，人工神经网络日益成熟并且大量运用于模拟电路故障诊断中，如BP网络、Hopfield网络和自组织网络。但对于FED驱动电路这种自主研制的规模较大的电路，仅采用如BP神经网络进行故障诊断，存在输入数目太多、结构规模大、训练时间太长等不足[2]。采用小波与神经网络相结合的方法，有效减少了神经网络的输入单元数，提高了网络的预测能力，可以很好地解决这些问题。本文采用小波包变换来提取模拟电路故障信号的特征，并通过归一化处理，将能量样本作为神经网络的输入，减小了神经网络的输入数目，从而简化了神经网络的结构。

1 基于小波包变换的FED驱动电路信号特征

1.1 小波包变换

目前，基于小波分析对电路的故障诊断方法中，大多都是对低频信号进行分解，而FED驱动电路信号的能量很多集中在高频部分，小波包变换是在小波分解的基础上，将高频系数继续分解，因此使用小波包分解更合适[3]。小波包的系数为

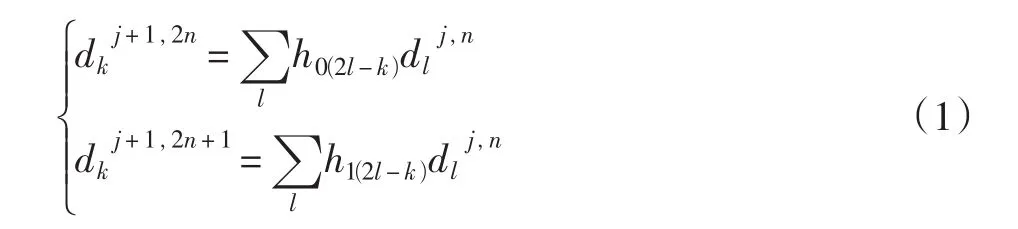
小波包分解实际上是对上层所有的子带都进行划分，对输出的电压信号进行高频分解，不但保留了小波分解的多分辨率特性，而且充分利用了输出信号的细节信息，成为有效的特征向量，从而提高了准确率。

1.2 FED驱动电路信号特征

FED驱动电路的行板扫描脉冲信号非常短，信号的局部特性较明显[4]。在靠近脉冲的时刻，信号的能量比较大，而在远离脉冲的时刻，信号的主要成分是平稳噪声以及低频干扰，信号能量较小。在FED驱动电路系统中，检测到的电阻容差的信号波形，在时域看来有时是非常相似的，通过小波包系数提供了许多有用的信息，完成特征信号的提取，确定故障信号。图1为电路在正常信号和故障信号下的波形特征。

从图1可以看出，信号的幅值和下降沿的变化速度有着极大的区别，运用小波包基提取信号在0.05～1.00 ms时间段的信息具有重要的意义。

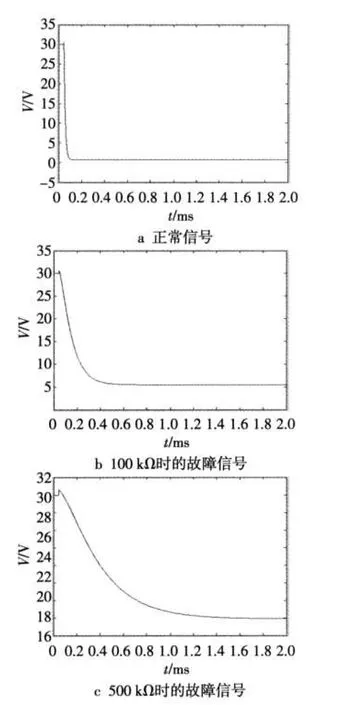
图1 FED驱动电路输出电压信号正常和故障时的波形特征

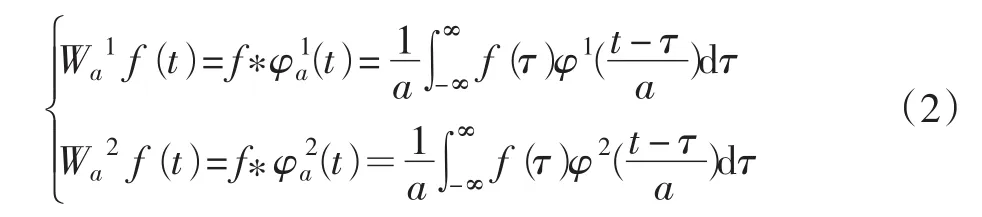
把小波函数看作平滑函数的导数，|Wa1f(t)|的极值点对应信号快变化点和慢变化点的位置[5]，通过对Wa2f(t)的值能判定拐点的位置，因此采用局部极值点对信号进行检测可以有效提取信号的特征信息。

2 信号的能量特征提取与故障识别

2.1 信号的能量特征提取

FED驱动电路的信号具有窄宽度和快速变化的特征，选择db2小波包对电压信号进行N层的小波包分解，分解成2N个子频带，取第N层尺度函数空间上的低频分解系数序列和高频分解系数序列[6]，各小波包分解系数序列的能量为

当系统发生故障时，会对各个频带内的能量产生较大的影响[7]，因此以能量为元素构造反映故障的特征向量T，T的构造如下

则T=(E1′,E2′,E3′,…）就是归一化后的故障特征向量。

2.2 故障识别

人工神经网络具有学习、记忆、识别和推理等功能，适合用作故障状态分类器。在人工神经网络的实际应用中，绝大部分的神经网络模型采用BP网络及其变化形式。BP网络是一种多层前馈型神经网络，又称误差反向传播算法网络。FED驱动电路故障诊断流程图如图2所示。

在对FED驱动电路的行板高压单元模块进行故障诊断时，通过小波包变换对数据进行预处理，确定可能出现的故障状态。将特征向量T输入到神经网络，并给定期望输出[8]。神经网络通过修改权值和阈值进行训练学习，最后再收敛到允许的误差范围之内。训练完成后，将实际测得的特征向量输入到训练过的神经网络，用于识别故障。

3 实验结果

将上述提到的方法运用于FED驱动电路的行板高压单元模块，电路图如图3所示。

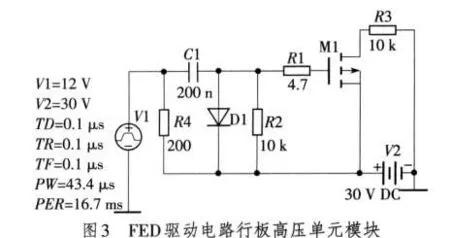
FED的行板是768路，行扫描电压是奇偶场，帧速60帧/秒（f/s），故采用幅度为12 V，宽度为1÷60÷（768÷2）=43.4 μs的窄带脉冲作为激励源，经过PSpice仿真，将仿真得到的波形数据导入Matlab中。对电路输出电压信号进行3层小波包变换，对各类故障进行容差分析并构成训练样本。图4～图6分别表示R3正常和故障时的原始信号和小波分解系数。

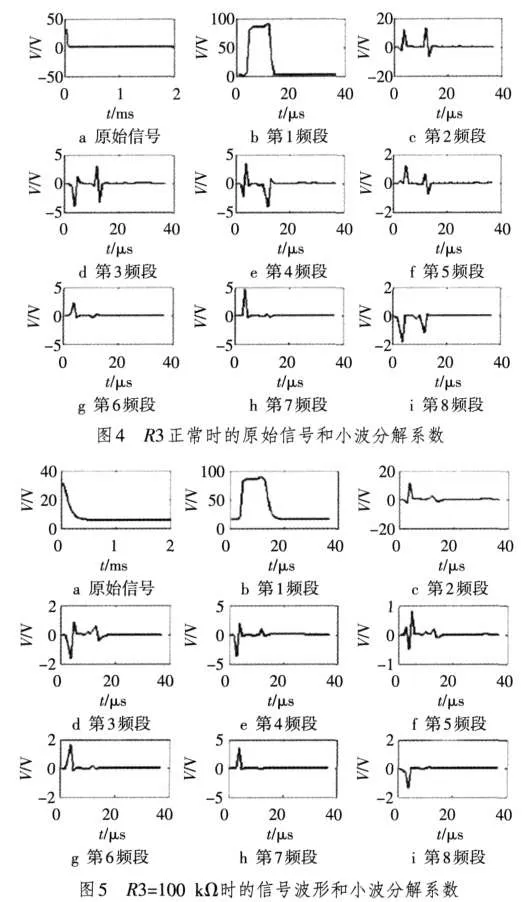
从图4～图6可以看出，小波分解系数的波形明显不同，R3正常时的特征值为T=[99.175 9，0.6361，0.062 9，0.065 2，0.004 1，0.009 3，0.036 6，0.009 9]，R3=100 kΩ时的特征值为 T=[99.748 8，0.193 7，0.006 3，0.025 9，0.001 4，0.004 4，0.016 8，0.002 6]，R3=500 kΩ时的特征值为 T=[99.939 7，0.042 9，0.000 7，0.013 3，0.000 2，0.000 5，0.002 2，0.000 5]。当电路发生故障时，小波系数有明显的变化。

电路的输出电压信号进行3层的小波包变换，将归一化处理后的故障特征向量作为神经网络的输入[9]。根据文献[10]的算法在Matlab中设计神经网络。对神经网络进行训练，隐含层和输出层的激励函数为非线性Sigmoid函数。以8个输入神经元，5个输出神经元，12个隐含层神经元构造神经网络。利用表1中的数据进行网络训练，不断调整修正网络权值和阈值，使误差满足要求。经过425次训练后，训练结果误差小于目标误差，数据见表1。