基于大小掩码区的图像修补研究
2011-03-15朱玉颖
张 岩,吴 斌,朱玉颖
(西南科技大学 信息工程学院,四川 绵阳 621010)
0 引言
现代生活中,图像已然成为不可或缺的生活元素,而数字图像更是渗透到生活中的方方面面,如数码相机、数字电视等等。但是,图像的传播过程中未免会发生数据丢失[1],影响图像显示效果,因此,各类数字图像修补算法也不断涌现。归纳各类算法,可发现图像修补过程往往是首先确定掩码区,而后结合其在图像中的位置,利用修补算法完成对图像的修补。但是,多数算法只是将掩码区统一归类,统一处理,而这也不可避免地造成修补过程效率降低。实际上,多数小掩码区域的修补并不需要复杂修补算法,利用简单便捷的结构修补便可实现,而大掩码区的修补可以利用纹理修补等较为复杂的算法来实现。此外,迭代次数上,小掩码区可以少一些,大掩码区则可以多一些。这样,通过掩码区将复杂与便捷算法相结合,既可提高效率,也可改善修补结果。
当然,手工也可以划分大小掩码区,但是如有大量图像需要修补,而其大小掩码区仍然利用手工确定,那势必会影响修补效率,而这也与图像修补领域掩码区的自动确定的发展方向相违背。因此,自动快捷的大小掩码区确定算法具有研究价值。
1 数字图像修补技术简介
图像修补技术发展已较为成熟,形成了一定的理论基础,并应用到生活中的多个方面,就目前取得的研究成果来看,图像修补技术可分为两个研究方向:结构修补和纹理合成。其中,结构修补利用图像周边信息,完成对图像缺失信息的修补,这与早期社会通过观察受损图像四周纹理与色彩信息,利用润色的方法完成修补的原理类似,如图1所示。
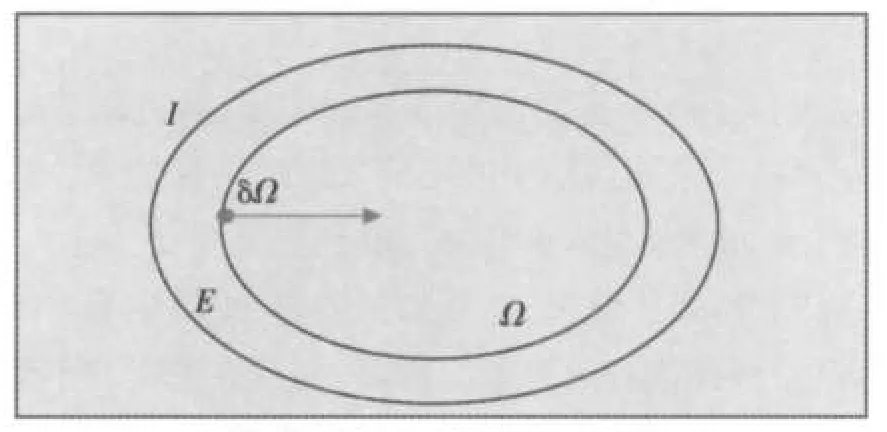
图1 结构修补原理图
图1中,I为待修补图像,Ω为修补区,δΩ为其边界,经典算法中,Bertalmio等人称其为等照度线(Isophtoes),E为可利用的图像修补区域,箭头指向梯度方向。修补过程用数学语言描述为

因此,修补过程就是不断更新Int(i,j)的过程。在结构修补领域,对Int(i,j)的更新方法有多种,如M.Bertalmio,G.Sapiro,V.Caselles一同提出的偏微分方程BSCB模型[2],以及T.Chan和J.Shen提出的更便捷的全变分Total Variational[3](简称TV)与曲率驱动扩散(CDD)模型[4]等,均产生很好的效果。此外,在这些经典算法的基础上,又延伸出了多种算法,如Masnou和Morel,Chan,Kang和Shen提出并研究的弹性函数图像修补模型[5],Esedoglu和Shen为图像修补提出的Mumford-Shah-Euler图像模型[6]等。
而后,Bertalmio等人又由起初像素(微观)层面,扩展到了样本块(宏观)的研究,即从结构层面扩展到纹理方向,开辟了纹理修补的方向。并且随着研究的深入,也提出了多种算法,如基于区域纹理合成的图像修补算法[7],以及基于样本块的图像修补算法[8]等。此外,现在流行的小波分析[9]、BP-神经网络[10]等高端技术也渗入这个行列中,开辟了图像修补研究的新方向。下面主要介绍两种文中利用的算法——TV模型与Manuel M.Oliveira提出的快速修补算法。
2 应用算法简介
2.1 TV模型
Rudin,Osher,Fatemi 3人观测到带噪图像整体变分明显比无噪图像大,便将整体变分方法引入图像处理领域[11],而Chan和Shen受到Rudin的启发,提出了两种图像修补算法,其中之一便是TV模型。该模型利用等照度线扩散方向的不同来进行图像的修补,有很好的效果,数学语言表述为其中

式中:λ发挥了一个重要的尺度参数作用,通过调节λ,能够在恢复结果中获得期望的不同尺度的图像信息。通过Euler-Lagrange方程求解上式,得到更新量Int(i,j),在经过迭代获得最终结果,需要指出的是,该模型为二阶偏微分方程,因此修补效率有所提高,而且在去噪和小区域的修补中效果明显,但是在连接破损边缘上,还存在一定问题[12]。
2.2 快速修补算法
该算法由Manuel M.Oliveira等人提出,其前提在于修补区域要满足局部小,以及人类视觉可以容忍在一定区域内的模糊,只要该区域未涉及到高对比度的边缘[13]。在此基础上,算法从像素入手,对于要修补的像素点,利用扩散核卷积该像素四周的像素,从而得到该点的值,之后进行迭代,直至达到满意的效果。更进一步说,算法就是利用n×n模板,从掩码区边界开始,对其周围进行卷积,并不断深入,直至整个掩码区全部被处理,然后再迭代多次,得到最终图像,用数学语言描述为
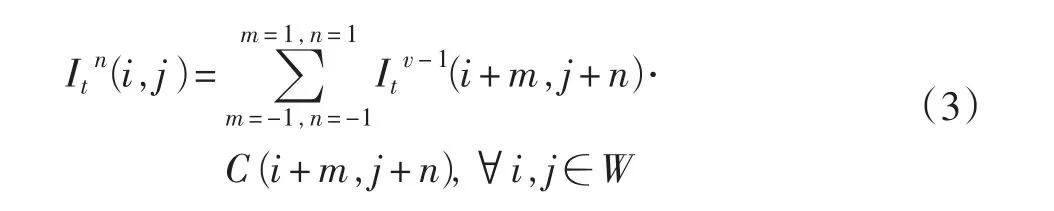
Ω为掩码区,即修补区域,I(i,j)为掩码区的像素值,C(i,j)为预设模板中的值,这里利用3×3模板,见图2。该算法与滤波器原理类似,掩码区为噪声成分,修补过程就是利用滤波器来去除这些成分的过程,并且同时还添加上了平滑、均值等效果,令修补区周围的信息得以延伸,从而达到修补的目的。

图2 模板C取值
3 划分大小掩码区
在处理掩码区前,需要了解关于连续性的问题。这里的连续性,指连续的亮点数量(二值化后图像中,值为1的区域为掩码区,即亮点区域),通过其与给定阈值的比较,得到其连续性强弱关系,即大于阈值则为强,小于阈值则为弱。对于要处理的掩码区,图像二值化后,观察得到的图像,不难发现大掩码区连续性强,小掩码区连续性弱。由此,得到掩码区划分流程:
1)给定一个阈值,将原图二值化,得到掩码区mask(亮区域)。
2)分配一片与原图大小相同的区域maskB,将其初始化为0(黑点),用来存储大掩码区。
3)搜索掩码区mask亮点所在的行r和列c,并将其存储起来。再建立两个新数组x(n)和y(n),且初始化x(1)=r(1),y(1)=c(1),以及累加器n=0。
4)按列(行)搜索下一个掩码区数据,如果r(i)-1=r(i-1),说明掩码区两个亮点相连,将数据保存x(i)=r(i),y(i)=c(i),并累加n=n+1,一直到此列(行)搜索完毕。之后,再判断连续性强弱关系,即n与阈值的大小关系,大于阈值则将存储maskB的数组x和y的相应像素位置标记为1(亮点)。
5)按照上面的步骤直至整幅图像扫描完毕,至此大掩码区全部确定。然后将mask中对应于大掩码所在的行列标注为0(黑点),并将其保存到masks,至此完成划分,得到大、小掩码区maskB与masks。效果如图3所示。

图3 掩码处理效果
但是,上面的算法仍然存在问题,如图4所示,原因在于部分掩码区按行(列)搜索时,连续性强,可是按列(行)搜索时,连续性则变弱。为了解决这个问题,可以将得到的maskB旋转90°,再按照步骤4)~5)运算,并将结果倒转90°,便可得到最终结果,如图5所示。
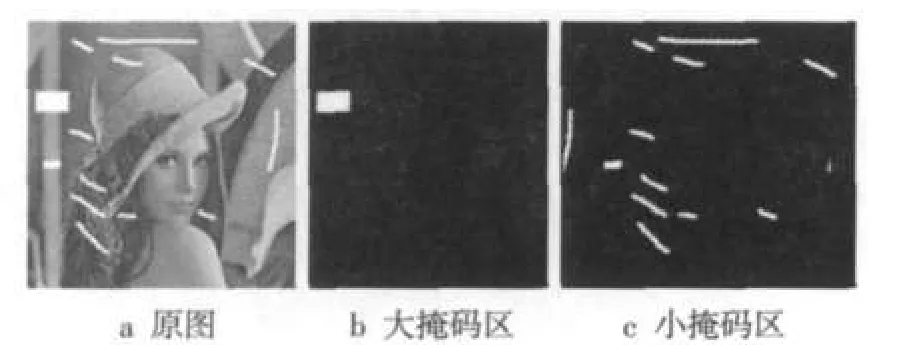
图4 算法存在问题示意

图5 改进后的效果
4 实验对比
采用Matlab7.0仿真,计算机配置为AMD双核4000+,2 Gbyte内存。由图6与表1可以看出,为达到一个较好的效果,TV算法的迭代次数要多一些,而快速图像修补算法则较少,且效果也有所提高,但仍然存在瑕疵,而利用改进算法进行修补,同TV和未划分前的修补图相比,修补效率与修补效果都有了改善。

图6 最终效果
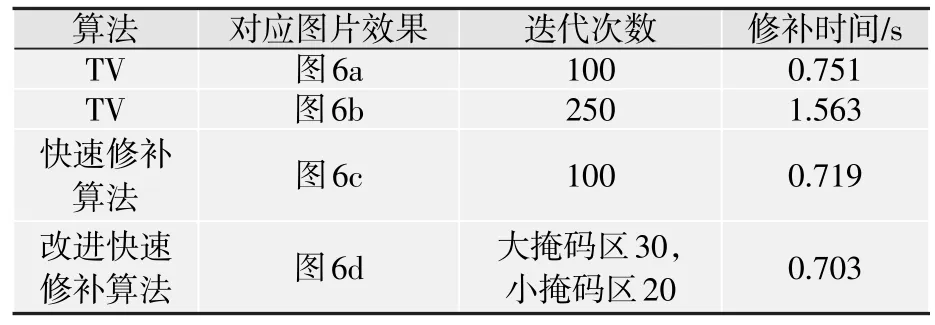
表1 实验结果
5 总结
本文算法的提出,主要在于为修补速率与修补效果的改善方向提出了一种新思路,且当一幅图片为灰度图或纹理不复杂的矢量图时,将会更快更好地达到要求。但是,由于它是图像修补领域中的新概念,仍然存在不足之处,如处理合并在一起的大小掩码区和部分不规则掩码区时,效果不明显,影响修补结果,因此仍有待完善。
[1]张利平,张红英,吴斌.基于多种边缘检测的视频划痕检测技术[J].电视技术,2010,34(1):85-87.
[2]BERTALMIO M,SAPIRO G,CASELLES V,et al.Image inpainting[C]//AKELEY K.Proc.ACM Conf.Comp.Graphics(SIGGRAPH2000).New Orleans,LA:ACM Press,2000:417-424.
[3]CHAN T F,SHEN J H.Mathematical models for local nontexture inpaintings[J].SIAM J.Appl.Math.,2001,62(3):1019-1043.
[4]CHAN T F,SHEN J.Non-texture inpainting by curvature driven diffusion(CDD)[J].Journal of Visual Communication and Image Representation,2001,12(4):436-449.
[5]CHAN T F,CHAN TF,KANG S H,SHEN J.Eider’s elastica and curvature based inpaintings[J].SIAM J.Appl.Math.,2002,63(2):564-592.
[6]ESEDOGLU S,SHEN J.Digital inpainting based on the Mumford-Shah-Euler image model[J].Euro.J.Appl.Math.,2002,13(4):353-370.
[7]付绍春,楼顺天.基于区域纹理合成的图像修补算法[J].电子与信息学报,2009,31(6):1319-1321.
[8]雷鸣,王春东,薛彦兵,等.一种新的样本块图像修补方法[J].光电子激光,2009,20(5):677-679.
[9]孙晓丽.偏微分方程和小波在图像修复与特征提取中的应用[D].西安:西安电子科技大学,2008.
[10]李宇鹏,王秋梅,孙红胜,等.基于RBF-BP神经网络的图像修补[J].燕山大学学报,2007,31(6):471-475.
[11]RUDIN L,OSHER S,FATERNI E.Nonlinear total variation based noise removal algorithms[J].Physica D,1992,60(1-4):259-261.
[12]庄红林,施国兴,范菁,等.基于轮廓-纹理分解的图像修补技术研究[J].昆明理工大学学报,2008,33(3):58.
[13]OLIVEIRA M M,BOWEN B,MCKENNA R,et al.Fast digital image inpainting[C]//Proc.The International Association of Sicence and Technology for Development Conference on Visualization,Imaging and Image Processing.Marbella,Spain:[s.n.],2001:261-266.
