参数化可配置IP核浮点运算器的设计与实现

刘竹松，陈平华，陈 璟

（广东工业大学 计算机学院，广东 广州 510006）

参数化可配置技术是指在集成开发环境下，利用设计中的可配置资源，根据需求重新配置一个运算系统，以实现兼顾高性能硬件设计和可配置特征的系统，即成为参数化可配置运算系统。参数化可配置系统的原理是：通过对参数可配置元件的利用，将硬件系统由专门的电路设计转变成为功能模块的组装，因此具有灵活、高效、低耗、易于开发与升级等特性。

在混沌电路、信号及图像处理中有大量的浮点数加、减、乘、除操作，浮点数本身的复杂性决定其需要专用的硬件来实现[1]。传统硬件电路的实现依靠手工搭建，过程复杂，存在电路参数分布性大、元器件老化、易受温度影响及通用性差等问题，尤其是对网格状多涡卷混沌吸引子的电路设计和调试需要花费更多时间。此外，要求电路设计者要有较高的技巧和经验[2]。基于IP核模块的设计方法是采用IP核模块而不是采用基本逻辑或电路单元作为基础单元，是以功能组装代替功能设计，用户只需通过设置参数即可方便地按需要定制自己的宏功能模块。使用户可以将精力集中于系统顶层及关键功能模块的设计上，致力于提高产品整体性能和个性化特性，加快了芯片设计速度，提高了芯片设计能力。

此外，IP核通常要经过严格的测试和优化，并且已经封装完毕,利用IP核进行电路设计可以在FPGA等可编程逻辑器件中达到最优的性能和最低的逻辑资源使用率，以保证电路的性能和质量。基于参数可配置IP核的浮点运算器的设计可大大提高混沌电路及其他电路设计者的电路设计能力，有力推动了混沌电路在相关领域的应用。

1 参数化IP核

IP核的本质特征之一是可重用性，在不同的应用场合对IP核功能、性能、面积及功耗等要求也不同，这就要求IP核具有较好的可伸缩性和灵活性。为了使IP核在使用中具有更好的灵活性和可配置性，IP核应该被设置为参数化可配置的。根据参数配置时机的不同，参数化IP核的配置参数可分为静态参数和动态参数[3]。

(1)静态参数：静态参数是指在系统运行前，一次性将参数化IP核的参数配置为系统所需的某个或数个功能，这些配置好的功能，在系统运行期间不会改变，直到系统完成任务后,参数化IP核才配置成为其他功能去完成其他任务。也就是说,当硬件要重新配置参数时，系统必须先停止运行，待参数配置完成后系统才能继续运行。

(2)动态参数：动态参数是在系统运行过程中，可随时重新配置参数化IP核的功能，参数配置与系统运行是同时的。因此，在设计IP核的动态参数时，必须先把参数配置所需的电路模块包含在其中，并将可配置的参数保存在寄存器中，这样在系统运行时才能随时配置参数调用所需的功能。图1为动态参数的控制结构。

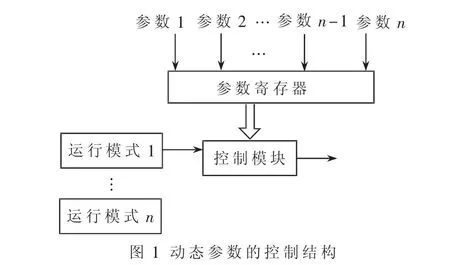
(3)动态参数与静态参数的比较：动态参数的使用大大提升了IP核的运行灵活性，但其缺点也很明显。因为动态参数属于“运行时配置”的参数。采用动态参数设计的IP核,在设计时已经将所有的功能模块包含在电路中，通过参数寄存器来实时选择IP核的功能，因此，电路设计功能越多、参数越复杂，其芯片面积的占用和功耗也越大。而静态参数属于“编译时配置”的参数[4]，它在流片之前就已经将IP核的参数确定好，因而在实现过程中不会产生冗余电路，减小了设计成本。

2 参数化浮点运算器IP核设计

在参数化浮点运算器IP核的设计中,由于浮点减法器与浮点除法器都可通过参数化浮点加法器和参数化浮点乘法器实现，故本设计只重点探讨参数化浮点加法器和参数化乘法器的优化算法和设计技术。

2.1 参数化浮点加法器设计

浮点加/减法在浮点运算中占有很大的比例,在浮点加法器的设计中，尾数的计算是影响浮点运算性能的关键，而其中进位运算对尾数计算速度影响最大。因此，围绕如何提高浮点运算器的进位产生速度，科研人员在传统串行的行波进位加法器的基础上，提出了一些并行快速产生进位的方法,如:超前进位加法器CLA(Carry Lookahead Adder)、条件进位选择CCS(Conditional Carry-Selection)加法器等。本文采用的是对超前进位加法器改进后的、适用于参数化浮点运算器设计的分块超前进位加法器BCLA(Block Carry Look-ahead Adder)。

2.1.1 分块超前进位加法器算法

图2是一个 4 bit超前进位加法器模块，通过将数个CLA分成相同大小分组级联，组间采用行波进位的方式连接，以加强加法器件的模块性。

设组间的进位传递函数为G*，进位产生函数为P*，若分组大小为4:如果进位输出是内部传递的，则G*=1;如果进位输入是内部产生的,则P*=1。组间进位的G*、P*计算如下：

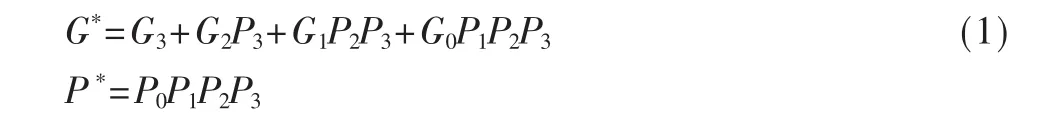
依据式(1)，组间产生和传递的进位，可以采用相类似的方式产生,通过增加一个组间CLA以组合方式设计成为分块超前进位加法器组合电路。图3为采用BCLA以及CLA组合设计的16 bit加法器逻辑图。对于n位操作数的加法，可将其分为 n/4个分组，每4 bit一个CLA的模块完成一次超前进位运算需要2ΔG的时间(假设每个门电路延迟为 ΔG)。其中需要 1ΔG的时间产生 Pi和Gi，2ΔG的时间来产生本位输出，因此，整个电路的总运算时间为：

从式(2)可以看出，与完全的行波进位加法器的延迟2nΔG相比，采用BCLA方法设计的加法器的延迟理论上只有其1/4，性能得到了很大的提升。

2.1.2 分块超前进位加法器设计

根据IEEE-754标准的浮点加/减法的基本原理[5]，对于两个浮点数的加/减法，可将其分解为8个步骤：符号运算、指数运算、尾数移位、尾数运算、规格化、指数调整、舍入、封装。然后根据这8个步骤,对浮点加/减法进行运算的细化。在细化流程的基础上，把尾数对位划分为对阶和移位，在符号运算电路中加入加减法操作的信号,根据IEEE-754标准的浮点格式的限制及异常处理，划分浮点数的加/减法运算电路的功能模块。图4为分块超前进位加法器的功能模块。

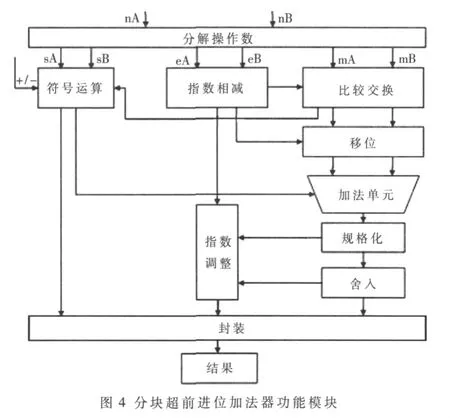
为了使基于VHDL设计的参数化IP核开发流程明确、设计目标清晰，需要在进行VHDL描述之前对浮点加法器的参数的提取进行研究，分析出可提取参数和可实现的参数。在浮点运算器中对参数的配置主要要求是：

(1)各参数之间的耦合度应该比较小；

(2)可进行参数配置的模块，能够显著改变浮点运算器的性能、面积、功耗等；

(3)参数化应该比较容易实现。

2.2 参数化浮点乘法器设计

浮点乘法在浮点运算器中的使用比例仅次于浮点加/减法，因此也是非常关键的浮点运算部件之一。按照IEEE-754标准，浮点运算被分为符号位运算、指数运算、尾数相乘三个步骤，从20世纪60年代至今，已经提出了许多种定点乘法运算单元的实现方法。各种乘法器运算方式都是先将乘法转换为加法，再通过快速求和的方法来得到最终的计算结果。本文采用的是适用于参数化浮点运算器设计的Booth算法。

(1)为解决有符号数乘法运算中复杂的符号修正问题，Booth提出了一种针对乘数进行编码的Booth编码。Booth编码在乘数最低位增加一个零值，在循环求部分积时，每次取乘数的相邻两位（基-4）进行判断，依据这两位的值，判断其部分积是被乘数的一倍或是两倍[6]。

Booth编码乘法运算可分三步进行：①产生部分积；②加法阵列累加部分积；③应用加法器求得最终结果。

采用Booth编码设计的乘法器原理如图5所示。

对于两个 32 位定点数 A=a31a30…a0，B=b31b30…b0，其中 a31、b31为符号位。有：

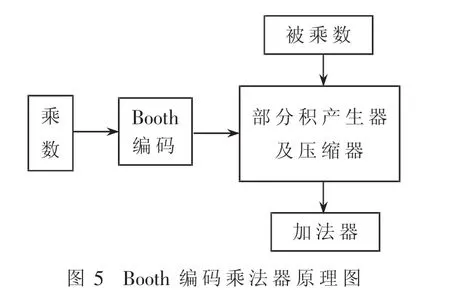
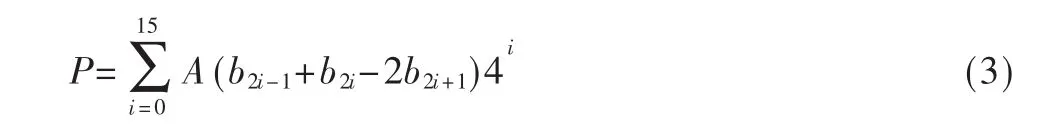
其中,X=b2i-1+b2i-2b2i+1是部分积。因此，可归纳出二阶Booth算法的重叠扫描操作如表1所示。

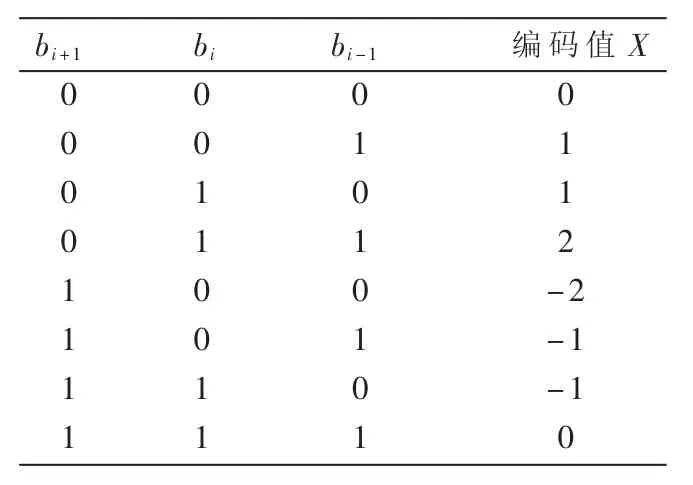
表1 二阶Booth算法操作

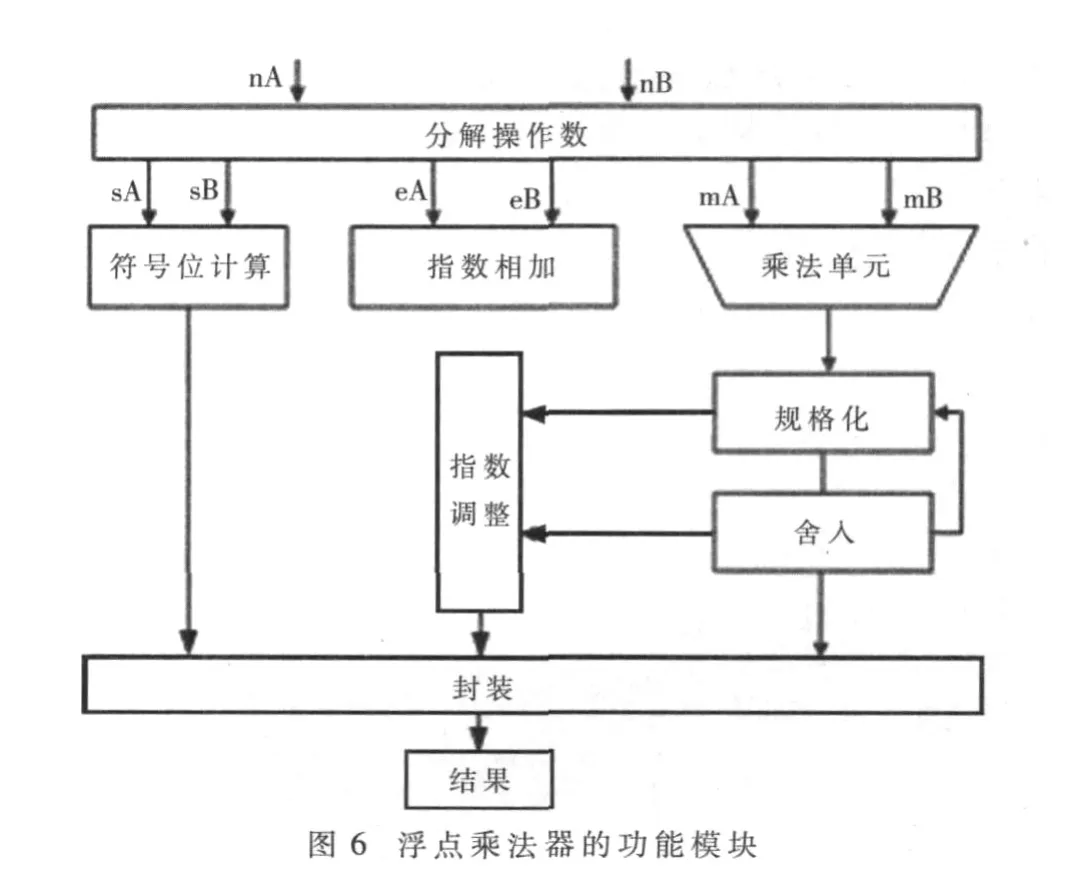
(2)根据IEEE-754标准的浮点乘法的基本原理，对于两个浮点数的乘法，可将其分解为7个步骤[7]：符号运算、指数运算、尾数移位、尾数运算、规格化、指数调整、舍入。根据这7个步骤，对浮点加/减法进行运算的细化，在细化流程的基础上，根据IEEE-754标准的浮点格式的限制及异常处理，划分浮点数乘法运算电路的功能模块。图6是浮点乘法器的功能模块设计。

3 综合与仿真

3.1 综合

综合是使用指定的元件，通过综合工具将一个设计从硬件描述(VHDL)转变为一个电路的过程,是VHDL在数字设计中不可缺少的一步[8]。而综合工具可大大缩短数字系统的设计周期，设计人员只需在高层对系统进行综合，可大大提高设计效率，缩减系统开发时间。

依据在参数化浮点加法器和浮点乘法器的参数配置，设定参数wE=8,wM=23,分别采用RCA和BCLA配置，使用Xilinx ISE 10.1在VirtexE XCV400E上分别综合一个单精度浮点加法器，综合结果如表2所示。

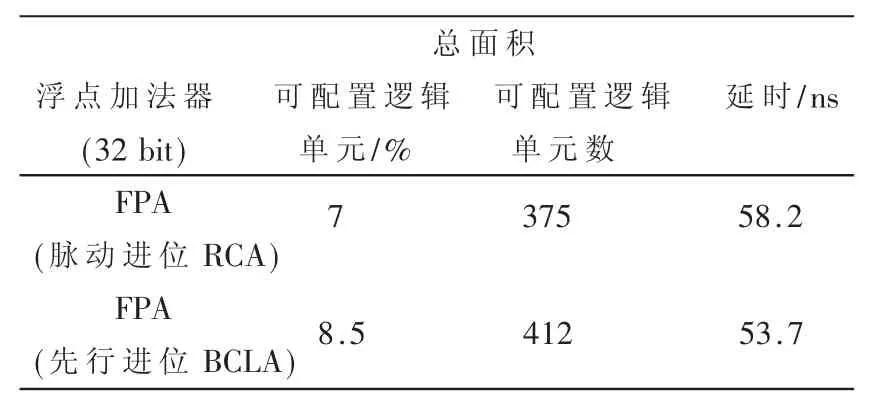
表2 32 bit浮点加法器综合结果

设定参数wE=8,wM=23,分别采用默认的方式和Booth配置综合一个单精度浮点乘法器综合结果如表3所示。

表3 32 bit浮点乘法器综合结果

3.2 仿真

仿真验证是保证一个项目设计成功的重要方法。IP核的设计过程中，利用可编程逻辑器件进行电路验证,对保证设计的正确性和投片成功十分重要。

依据仿真的基本方法，依照自底向上的仿真流程，在ModelSimPE环境下，对各模块进行仿真验证。图7～图9给出了仿真验证的实例。其中，RCA模块采用wM参数赋值8 bit，综合成一个 8 bit行波进位加法器，进行独立的仿真验证；Booth模块采用wM参数赋值8，综合成一个8×8位乘法器，进行独立的仿真验证。

本文对参数化IP核、浮点运算器设计的相关技术以及参数化在浮点运算器设计中的应用，作了比较深入的研究。给出了参数化IP核的设计方案和设计流程。依照IEEE-754标准，分析了浮点加/减法、乘法的基本原理，并细化设计了适合参数化的浮点运算器流程；最后在Xilinx ISE 10.1和Modelsim 6.6a平台上进行了综合与仿真。

[1]Liu Zhusong.A novel fourth-order chaotic circuit and its implementation[C].9th International Conference for Young Computer Scientists,2008:3045-3050.

[2]周武杰,禹思敏.基于现场可编程门阵列技术的混沌数字通信系统——设计与实现[J].物理学报,2009,58(1).

[3]Zhao Junchao,Chen Weiliang,WEI Shao Jun.Parameterized IP core design[C].Proceedings:4th International Conference on,2001:744-747.

[4]徐晨,袁红林.基于 VerilogHDL的IP核参数化设计[J].微电子学与计算机,2005,12(1):85-88.

[5]陈弦,张伟功,于伦正.并行浮点加法器架构与核心算法的研究[J].计算机工程与应用,2006,17(1):53-55,75.

[6]Chen Pinghua,Zhao Juan.High-speed parallel 32×32-b multiplier using a radix-16 booth encoder[C].Third International Symposium on Intelligent Information Technology Application Workshops,2009:406-409.

[7]周德金,孙锋,于宗光.一种32位高速浮点乘法器设计[J].电子与封装,2008,65(1):35-38.

[8]江思敏.VHDL数字电路及系统设计[M].北京：机械工业出版社,2006.