基于Copula-GARCH模型的外汇期货最优套期保值比率研究

马超群，王宝兵

（湖南大学 工商管理学院，长沙 410082）

0 引言

外汇期货是指交易双方约定在未来某一时间，依据约定的比例，以一种货币交换另一种货币的标准化合约，是期货市场一个重要的交易品种。它是以汇率为标的物的期货合约，能用来规避外汇风险。随着全球经济一体化和对外贸易的深入发展，我国企业特别是跨国公司、进出口型公司将面临更为动荡的外部市场环境，同时承受来自产品市场和要素市场的各种风险，其中外汇风险是企业必须面对的重要风险之一。那么，如何降低由于汇率变动可能带来的风险，乃是我国企业迈向国际化过程中不容忽视的重要课题之一。因此，使用外汇期货进行套期保值分析，对于我国企业减少套期保值成本，从而规避外汇风险，具有十分重要的研究意义。

期货市场的风险转移功能主要通过套期保值策略实现，而套期保值理论的核心是套期保值比率的确定。现有研究主要可以分为以下两大类：一类是从组合收益风险最小化的角度，研究最小风险套期保值比率；另一类是综合考虑组合收益和组合收益的方差，从效用最大化的角度研究均值-风险套期保值比率。本文研究属于第一类，即从组合收益风险最小化的角度研究外汇期货最优套期保值比率问题。

本文首先简要介绍最小方差套期保值比率和三类套期保值模型：ECM-GARCH模型、CCC-GARCH模型和Copula-GARCH模型，其次使用欧元、英镑现货和期货数据进行实证分析，进而计算最优套期保值比率，并对比分析上述三类模型的套期保值效果。

1 模型及方法

1.1 最小方差套期保值比率

考虑一个包含Cs单位的现货多头头寸和Cf单位的期货空头头寸的资产组合，记St和Ft分别为t时刻现货和期货的价格,则此资产组合的收益ΔVH为：

式(1)中：ΔSt=St-St-1,ΔFt=Ft-Ft-1。

那么，资产组合套期保值的风险为：

Johnson(1960)通过最小化期货与现货组合的方差提出了最小方差套期保值比率，其计算公式为：

考虑到协方差和相关系数之间的关系，式(3)可变为：

其中 ρΔSt,ΔFt表示现货和期货的相关系数，σΔSt和 σΔFt分别表示现货和期货的标准差。

1.2 ECM-GARCH模型

Engle(1982)最先提出了自回归条件异方差模型(A简称ARCH)，并由Bollerslev(1986)发展成为GARCH-广义自回归条件异方差模型，该模型特别适用于对金融时间序列数据的波动性和相关性进行建模，一般由两个方程组成，一个是条件均值方程，一个是条件方差方程，GARCH(p,q)模型的表达式为：

其中Rt是t时刻的收益率，ut是条件均值，残差εt服从均值为0，方差为的正态分布。ω为常数项，p是GARCH项的阶数，q是ARCH项的阶数，Ωt-1为期信息集。为保证GARCH过程是宽平稳的，需要对模型参数施加如下约束条件：αi≥0，βj≥

Kroner和Sultan(1993)认为GARCH模型忽略了时间序列间存在的协整关系，于是将考虑了协整关系的ECM模型和GARCH模型结合成为ECM-GARCH模型，该模型的表达式为：

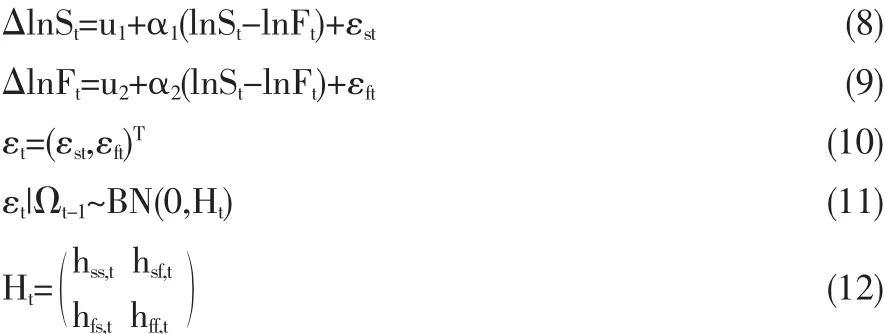
其中△lnSt和△lnFt分别为t时刻现货和期货的一阶差分对数收益率，u1和u2、α1和α2均为常数项，残差εt服从均值为0，条件协方差为Ht的二元正态分布，Ωt-1为t-1时刻信息集，hss,t和hff,t分别为t时刻现货和期货的方差，而hsf,t为t时刻现货和期货的协方差。

1.3 CCC-GARCH模型

Bollerslev(1990)在BGARCH模型基础上提出了静态条件相关模型 (Constant Conditional Correlation，简称CCC模型)，该模型可表示为：

其中 Rt=(△lnSt,△lnFt)T,ut=(ust,uft)T，εt=(εst,εft)T,Ωt-1为期信息集，BN为二元正态分布，Ht为时变正定的条件协方差矩阵，Dt=diag(hi,t)是条件方差取对角项所形成的n×n的对角矩阵，R是固定的n×n条件相关系数。Bollerslev假定残差εst和εsf之间的相关系数ρst为常数，此时，Ht可表示为：

式(17)中t时刻现货方差hss,t、期货方差 hff,t、现货和期货协方差hsf,t分别由以下等式给出：

1.4 Copula-GARCH模型

Slkar(1959)最早提出Copula函数的概念。Slkar指出，Copula函数可以理解为“连接函数”，它把多维随机变量的联合分布用其一维边际分布连接起来。对于一个具有一元边缘分布的联合分布F1,F2,…,Fn函数F，一定存在一个Copula函数，满足：

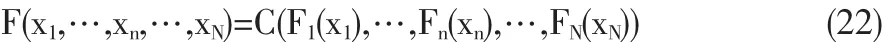
若F1(x1),…,Fn(xn),…,FN(xN)连续，则C唯一确定；反之，若F1(x1),…,Fn(xn),…,FN(xN)为一元分布，那么由上式定义的函数F是边缘分布F1(x1),…,Fn(xn),…,FN(xN)的联合分布函数。由此可见，Copula函数描述了变量间的相关结构，从概率角度上反映了变量间的相关性，为求取联合分布函数提供了一条便捷的通道。

运用Copula理论构建金融模型，可分为以下两个步骤：

第一，确定边缘分布。由于金融时间序列多呈现随机波动特性和尖峰厚尾等现象，而GARCH类模型特别适用于对金融时间序列数据进行建模，可用来估计或预测其波动性和相关性。因此，本文使用GARCH(p,q)模型描述变量的边缘分布。

第二，定义一个适当的Copula函数，以便描述边缘分布的相依结构。本文研究的是现货和期货两类资产价格在上升和下降时的套期保值比率，因此选用 Gumbel Copula和Clayton Copula函数度量现货和期货间的尾部相关性。

Copula-GARCH模型是将GARCH模型和Copula函数结合起来，以此分析变量间相关关系和分布特性，其中GARCH模型用于描述各变量的边缘分布，而Copula函数则用于连接各变量的边缘分布以得到总体的联合分布。

由于本文研究涉及现货和期货两个随机变量，因此采用二元Copula-GARCH模型。结合Copula函数和GARCH模型，可得到如下一般形式的模型：

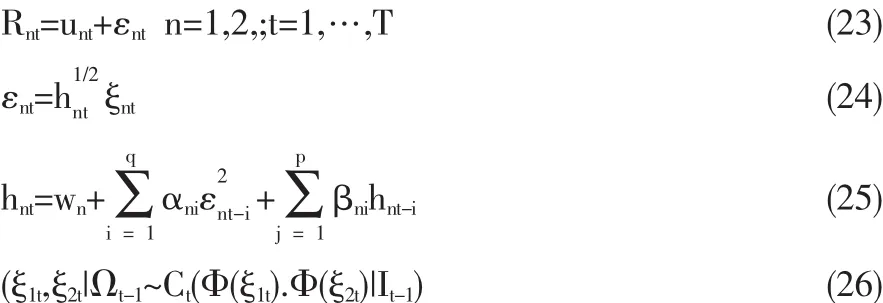
其中Rnt表示t期第 n个随机变量，unt和 hnt分别表示t期第n个随机变量的均值和方差，而εnt和ξm则分别表示t期第n个变量的残差和标准残差，ε1t和ξ2t均独立同分布，Ωt-1表示t-1期信息集，Copula函数Ct(Φ(ξ1t).Φ(ξ2t)|It-1)表示t期两个随机变量R1t和R2t之间的相关结构，Φ(·)为标准一元正态分布函数。

Archimedean Copula函数有一个重要特性，即Kendall秩相关系数均τ为单参数Copula函数参数θ的解析函数。对于Gumbel Copula函数，Kendall秩相关系数τ、参数θ及上尾相关数λu三者的关系是：θ=1/(1-τ)，λtt=2-21/θ；对于Clayton Copula函数，Kendall秩相关系数τ、参数θ及下尾相关数λl三者的关系是：θ=2τ/(1-τ)，λl=2-1/θ。

由于本文考虑到现货和期货资产价格在上升和下降时的不同情况，因此我们选取上尾相关数λu和下尾相关数λl的平均数作为期货和现货的相关系数，以计算最优套期保值比率。此时，最优套期保值比率的计算公式为：

其中λit和λl分别表示上尾相关数和下尾相关数，而σs,t和σf,t分别表示现货和期货时变的标准差。

2 实证分析

2.1 数据来源及处理

本文选取自2007年5月1日至2010年4月30日期间欧元、英镑现货和期货数据，除去缺失数据，共计751对日数据，其中2007年5月1日至2009年12月31日共计668对日数据为样本内数据，用于计算套期保值比率；2010年1月1日至2010年4月30日共计83对日数据为样本外数据，以此对比各模型的套期保值效果。外汇现货数据是从美国联邦储备委员会网站上（http://www.federalreserve.gov/econresdata/releases/statisticsdata.htm）下载，为纽约中午电汇买入价，均以一外币折合一美元表示。外汇期货数据来源于美国芝加哥商品交易所CME国际货币市场（IMM）日交易报告，选取欧元（EU）、英镑（GBP）的收盘价，具体是从华尔街日报上手工收集，均以一外币折合一美元表示。为避免价格异动和实物交割，不选取交割月份的期货合约，因此，前一年12月份和本年1、2月份交易本年3月份的期货合约，本年3、4、5月份交易本年6月份的期货合约，本年6、7、8月份交易本年9月份的期货合约，而本年9、10、11月份交易本年12月份期货合约，这样就可以构造出一个连续的期货价格序列。

在平稳性检验和协整检验之前，我们首先计算出各货币收益率序列的“对数收益率”，即对原序列作一阶对数逐期查分，△lnRt=lnRt-lnRt-1，再对各收益率序列进行统计特征描述，从而得到各货币收益率数据描述统计表，具体结果见表1。

从表1中可见，对比各货币收益率的均值发现欧元、英镑现货和期货收益率的均值在0附近，其中欧元现货和期货的均值大于0，而英镑现货和期货的均值小于0，欧元现货均值最高，其值为7.86E-05，而英镑期货收益率均值最低，其对应的值为-0.000320。在偏度上，欧元现货的偏度值大于零，右偏，而欧元期货和英镑现货、期货收益率的偏度值均小于零，左偏。在峰度上，各货币现货、期货收益率均大于3，说明它们都呈现出尖峰厚尾的形态。J-B统计量检验证实这四个收益率序列都不符合正态分布。总之，欧元、英镑的现货和期货收益率序列均呈现时变、尖峰厚尾等分布特征。

表1 收益率序列基本统计特征

2.2 平稳性及协整检验

首先，对各货币收益率序列分别进行单位根检验，检验结果表明，在1%显著性水平下，欧元现货和期货收益率序列ADF统计量的值分别为-25.71276、-25.51398，均小于1%显著性水平下对应的临界值-3.439940和-3.439940，说明欧元现货和期货收益率序列均为平稳序列；对英镑现货和期货收益率序列进行单位根检验，ADF统计量的值分别为-25.21986和-24.03839，同样小于1%显著性水平下对应的临界值-3.439940和-3.439940，这表明英镑现货和期货也是平稳性序列。

其次，采用Engle-Granger提出的E-G两步法来检验各货币现货和期货之间的协整关系。E-G两步法协整检验从检验对象上可分为两种：一种是基于回归系数的协整检验，即Johansen协整检验；另一种是基于回归残差的协整检验，如CRDW检验、DF检验、ADF检验。本文采用第二种方法检验现货和期货间的协整关系。先使用OLS线性回归方法对各货币现货和期货收益率进行简单线性回归，再对线性回归方程的残差进行单位根ADF检验，计算结果表明，在1%显著性水平下，两个线性回归方程的残差ADF统计量的值分别为-23.92534和-23.30802，均小于1%显著性水平对应的临界值-3.439970和-3.439970，因此可以认为线性回归后方程的残差为平稳序列，由此表明欧元的现货和期货以及英镑的现货和期货之间都存在长期稳定的协整关系。

2.3 Copula-GARCH模型估计

表2 GARCH(1,1)模型估计结果

我们首先分别对各货币收益率序列进行线性回归分析，建立均值方程，并检验残差的自相关性和ARCH效应，结果表明，各均值方程不存在自相关性，但都存在ARCH效应。为消除均值方程存在的ARCH效应，我们使用GARCH(p,q)模型描述各货币现货和期货收益率序列的边缘分布。一般而言，GARCH(1,1)模型形式最简单，在实际应用中也最为常用，能够很好地满足建模要求，因此本文选用GARCH(1,1)模型描述变量的边缘分布，模型估计结果见表2。

从表2中可见，除常数项外，GARCH(1,1)模型的参数在5%显著性水平上均是显著的。检验各货币现货和期货收益率序列GARCH(1,1)模型的自相关性和ARCH效应，检验结果发现均不存在序列自相关和ARCH效应，且各模型α+β＜1，说明GARCH(1,1)模型是宽平稳的，且拟合效果较好，能够较好地描述各货币现货和期货收益率序列的边缘分布。使用QQ图拟合各GARCH(1,1)模型标准残差的分布，结果表明，使用正态分布拟合效果较好。再对标准残差序列进行概率积分变换，运用K-S检验方法检验概率积分变换后的序列是否服从(0,1)均匀分布从而得到K-S检验统计量对应的概率值，从表2中可见，K-S检验统计量对应的概率值均不显著，因此无充分理由拒绝“变换后的序列服从(0,1)均匀分布”的零假设。此外，检验概率积分变换后标准残差序列的自相关性，结果表明，各标准残差序列均不存在自相关，说明概率积分变换后的序列是相互独立的，因此使用GARCH(1,1)模型估计得到边缘分布的标准残差序列均服从i.i.d(0,1)均匀分布，满足Copula-GARCH的建模要求。

利用MATLAB 7.0软件编程，分别估计欧元现货和期货以及英镑现货和期货之间的Kendall秩相关系数，并计算对应的Gumbel Copula和Clayton Copula函数的尾部相关数，计算结果详见表3。从表3中可见，英镑现货和期货的Kendall秩相关系数较高，为0.73697，高于欧元现货和期货对应的Kendall秩相关系数的值0.69033，说明英镑现货和期货间的相关性比欧元现货和期货间的相关性更强；此外，对比Gumbel Copula和Clayton Copula函数估计的尾部相关数，英镑现货和期货的尾部相关数分别为 0.80000和 0.88365，高于欧元现货和期货尾部相关数对应的估计值0.76057和0.85601，说明英镑现货和期货收益率序列的尾部更敏感，更易受到收益率波动的影响。

表3 Copula函数估计结果

2.4 不同模型套期保值比率计算结果

本文使用Gumbel Copula和Clayton Copula函数的尾部相关数代替传统的线性相关数作为各货币现货和期货收益率序列之间的相关系数，再利用GARCH(1,1)模型计算现货和期货收益率序列的波动率，将其带入最优套期保值比率方程(27)，从而求出Copula-GARCH模型的套期保值比率，并与CCC-GARCH模型和ECMGARCH模型计算出的套期保值比率相比较，计算结果如表4所示。

表4 不同模型套期保值比率估计

由于各模型计算出的套期保值比率均为动态套期保值比率，因篇幅限制，无法具体列出，因此本文只对比其均值和方差。从表4中可见，对于欧元期货，Copula-GARCH模型套期保值比率的均值和标准差最小，其值分别为0.815335和0.046425，均小于其他模型对应的计算结果，其次为CCCGARCH模型，而ECM-GARCH模型计算出的均值最大，且标准差最大，其值分别为0.961102和0.080238，由此可见，使用Copula-GARCH模型能够获得最优套期保值比率，且波动性最小；对于英镑期货，Copula-GARCH模型计算的套期保值比率均值和标准差最小，其值分别为 0.847049和0.065567，其次为CCC-GARCH模型，而ECM-GARCH模型计算出的均值和标准差最大，同样说明Copula-GARCH模型能够获得最优套期保值比率，且波动性最小。综上，运用Copula-GARCH模型计算出的套期保值比率最优，波动性最小，能够显著降低套期保值者的套期保值成本。此外，对比欧元和英镑期货各模型计算出的套期保值比率的均值和标准差，结果表明，欧元期货相对于英镑期货具有较小的套期保值比率且波动性相对较小，说明相对于英镑期货而言，对欧元期货进行套期保值，其套期保值成本低且风险较小。

2.5 套期保值效果对比

Lien(2002)给出了套期保值绩效的衡量指标，即和未参与套期保值时收益方差相比，参与套期保值后收益方差的减少程度，计算公式如下：

其中，He为套期保值绩效指标，Var(ut)为未进行套期保值现货收益率的方差，Var(ht)为套期保值组合收益率的方差。套期保值绩效指标He越大，说明其套期保值效果越好。不同模型套期保值效果的计算结果见表5。

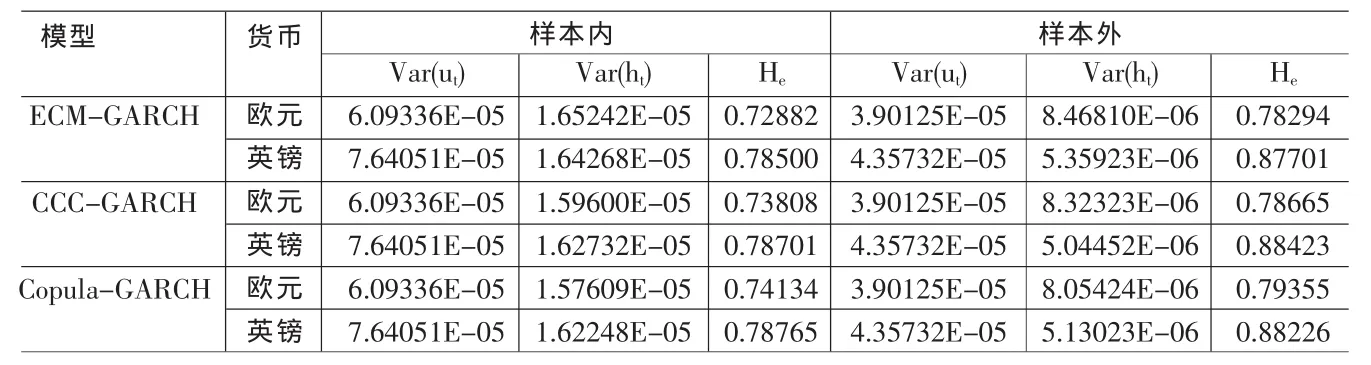
表5 不同模型套期保值效果对比

从表5中可见，在样本内，对于欧元期货，Copula-GARCH模型的套期保值绩效He最大，其值为0.74134，说明其套期保值效果最好，其次为CCC-GARCH模型，而ECMGARCH计算的套期保值绩效He最小，其值为0.72882，说明其套期保值效果最差；对于英镑期货，也可以得到同样结论。在样本外，对于欧元期货，Copula-GARCH模型的套期保值绩效He最大，其值为0.79355，说明其套期保值效果最好，其次为CCC-GARCH模型和ECM-GARCH模型；对于英镑期货，CCC-GARCH模型的套期保值绩效He的值为0.88423，略大于Copula-GARCH模型对应的值0.88226，说明CCCGARCH模型在样本外具有较好的套期保值效果，而ECMGARCH模型的套期保值绩效He最小，其套期保值效果相对较差。此外，样本外的套期保值效果好于样本内的套期保值效果；在样本内和样本外，对比欧元期货和英镑期货的套期保值绩效He，计算结果表明，英镑期货的套期保值绩效He均大于欧元期货的套期保值绩效He，说明使用不同模型对英镑期货进行套期保值，套期保值效果好于欧元期货的套期保值效果。

总之，与CCC-GARCH模型和ECM-GARCH模型相比，运用Copula-GARCH模型能获得相对较好的套期保值效果。

3 结论

最优套期比率的确定是套期保值操作中的一个十分重要的问题。本文使用Copula-GARCH、CCC-GARCH和ECMGARCH等三类模型分析比较了欧元和英镑两类期货的动态套期保值比率，并且评价了它们的套期保值效果，通过实证分析得出了如下结论：

（1）欧元现货和期货收益率以及英镑现货和期货的收益率均为平稳性时间序列，且相同货币的现货和期货收益率之间存在协整关系，具有长期的稳定性。

（2）运用Copula-GARCH模型计算出的套期保值比率最优，且套期保值效果相对于其它两个模型而言较好。在实际套期保值操作过程中，企业可考虑使用Copula-GARCH模型估计的套期保值比率来规避外汇风险，从而降低套期保值成本，获得较好的套期保值效果。

由于本文未考虑到交易成本、资金限制等现实问题，且只考虑了一对一的套期保值策略，因此仍存在一些不足。未来研究将考虑以上因素深入探讨最优套期保值比率问题，使其更符合企业运用外汇期货进行套期保值的实际需要。

[1]Ederington L H.The Hedging Performance of the New Futures Markets[J].Journal of Finance,1979,34(1).

[2]Embrechets P.,Mcneil A.Straumann D.Correlation and Dependence in Risk Management:Properties and Pitfalls[J].RISK,1999.

[3]Power,GJ,D.V.Vedenov.The Shape of the Optimal Hedge Ratio: Modeling Joint Spot-futures Prices Using an Empirical Copulagarch Model[C].Proceedings of the NCCC-134 Conference,St.Louis, Missouri,2008.

[4]YiHao Lai,Cathy W.S.Chen,Richard Gerlach.Optimal Dynamic HedgingVia Copula-threshold-GARCH Models[J].Mathematics and Computers in Stimulation，2009,(79).

[5]韦艳华,张世英.金融市场的相关性分析:copula-garch模型及其应用[J].系统工程,2004,22(4).

[6]赵家敏,沈一.股指期货最优套期保值比率:基于Copula-GARCH模型的实证研究[J].武汉金融,2008,(5).

[7]王玉刚,迟国泰,杨万武.基于copula的最小方差套期保值比率[J].系统工程理论与实践,2009,29(8).

[8]Johnson,L.L.The Theory of Hedging and Speculation in Commodity Futures[J].Review of Economic Studies,1960,(27).

[9]Engle,R.Autoregressive Conditional Heteroskedasticity with Estimates of the Variance of U.K.Inflation[J].Econometrica,1982,(50).

[10]Bollerslev,T.Generalized Autoregressive Conditional Heteroscedasticity[J].Journal of Econometrics,1986,(31).

[11]Kroner,K.F.,Sultan,J.Time-varying Distributions and Dynamic Hedging with Foreign Currency Futures[J].Journal of Financial and Quantitative Analysis,1993,(28).

[12]Bollerslev,T.Modeling the Coherence in Short-run Nominal Exchange Rates:Multivariate Generalized ARCH Approach[J].Review of Economics and Statistics,1990,(72).

[13]SklarA.Functions de Repartition an Dimensions et Leursmarges [J].Publications de Linstitut de.Statistique de L’Universite de Paris,1959,(8).

[14]Lein D,Tse Y K,Albert K C.Evaluating the Hedging Performance of the Constant Correlation GARCH Model[J].Applied Financial Economics,2002，12（11）.