原子质量的相对论效应和应用

朱正和，傅依备，蒙大桥，唐永健

(1.四川大学原子分子物理所，成都 610065;2.中国工程物理研究院，四川 绵阳 621900)

原子质量的相对论效应和应用

朱正和1，傅依备2，蒙大桥2，唐永健2

(1.四川大学原子分子物理所，成都 610065;2.中国工程物理研究院，四川 绵阳 621900)

应用相对论理论(Dirac)来计算 C、O、S、Se、Te、Sm和Pu原子的相对论和非相对论的电子状态和能量，比较相对论和非相对论的能量差别后得到:如果以 O原子的相对论和非相对论能量差为1，则 S、Se、Sm和Pu原子的相对论和非相对论能量差分别为17.5、479、6781和46166。就钚和氧相比，质量的相对论效应增加46166倍。Pu的相对论的和非相对论的能量的差占总能量的8.72%，所以对重元素，应用相对论的计算是很必要的。

Dirac理论;质量的相对论效应;钐和钚原子

1 前言

由于在相对论中，时间与空间的等价性，所以，对于相对论而言，则有量子力学方程必须服从Lorentz covariance协变，同时，和空间反转的对称性一样，也有时间反转的对称性。同时考虑空间和时间的对称操作后的群，称为全对称群，所以必须用全对称群的 Dirac 理论［1～3］.

在非相对论中，哈密顿算符不含自旋，即自旋与空间的对称性分开，正如LS偶合中，轨道角动量和自旋角动量是两个独立的运动常数。而在相对论中，自旋对称已失去意义。例如，在非相对论中，H2O是C2V群，而在相对论中，要由双群代替，并引入新元素¯Ε，对称元素增加1倍，而不可约表示增加1个，这第五个不可约表示称为费密子不可约表示(fermion表示)，它可由费密函数展开。而单群C2V的不可约表示称为玻色子不可约表示。而对于原子可有O(n)和对应的双群O'(n)。

应用相对论理论(Dirac)来计算 C、O、S、Se、Te、Sm和Pu原子的相对论和非相对论的电子状态和能量，比较相对论和非相对论的差别，考查质量的相对论效应。

2 相对论量子力学方法［5，6］

在相对论Dirac－Fock(MCDF)理论中，相对论轨道即单电子轨道波函数即角动算符和的本征函数，也是相对论宇称算符的本征函数。在坐标表象中，Dirac 轨道表示为

式(1)中，n代表主量子数;k代表相对论角量子数，它是一个复合量子数，可以同时表示单电子轨道波函数的角动量和宇称性，即，分别代表单电子的角动量和z分量分别是和m。Pnk(r)和Qnk(r)分别是径向波函数的大小量，由全部单电子轨道波函数反对称化乘积可以建立多电子总波函数，即所谓的组态波函数(configuration state function，CSF)，而组态波函数 |γPJM〉是宇称算符 ^P、总角动量算符^j2和^Jz的本征函数:

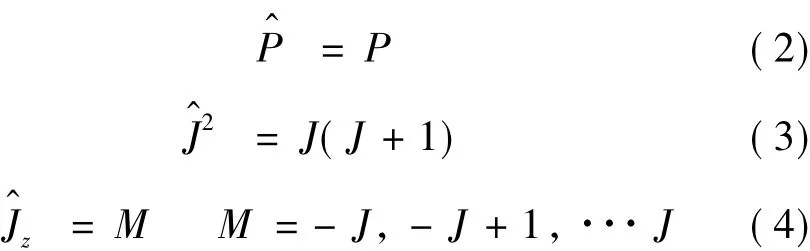
原子态波函数(atomic state function，ASF)可在组态波函数的组基上线性展开，即ASF是P、J和M相同的CSF的线性迭加:

式(5)中，crΓ是组态混合系数;N电子的Dirac－Coulomb哈密顿量为

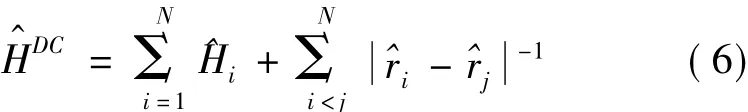
式(6)中，第一项 H^i是第i个电子单体作用的贡献，它包括除去电子静止能量c2后单电子动能及电子与核的相互作用势能，并由下式给出

式(7)中，c是真空中光速;α是Dirac矢量矩阵，α ={αi，i=1，2，3} ，其标准表示为

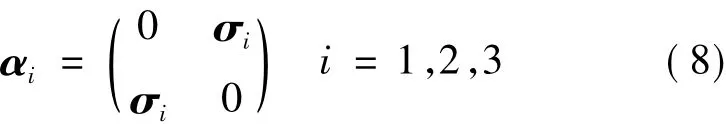
σi是Pauli矩阵，β是Dirac标量矩阵，其形式为

Vnuc.(ri)是核势场，在不考虑核的体积效应情况下，取Coulomb场形式－Z/r。

3 计算结果

计算C、O、S、Se、Sm和Pu原子的相对论和非相对论的电子状态和能量，比较相对论和非相对论的差别，考查质量的相对论效应。

为了比较同族而不同周期的原子的质量的相对论效应，计算了O、S和Se原子，见表1到表3。其中电子状态分别表示相对论的和非相对论的。已知氧原子基电子组态为，其非相对论的LS偶合得到的电子状态为和，而有三个光谱支项，相对论的电子只有总角动量有效，例如，对，其2和+分别表示相对论的总角动量为2和宇称为偶宇称，而对应的非相对论状态为。表中给出相对论和非相对论的和两者能量的差，都为原子单位au。

相对论和非相对论的能量的差，对于O原子为0.0558 到0.0561;对于 S 原子分别为 0.9754 到0.9764;对于 Se 原子分别为26.771 到 26.777 ，如果以O原子的能量的差为1，则S和Se原子的能量差分别为17.5和479。所计算的光谱支项能量的差，对O、S和Se原子都与实验值比较相合。

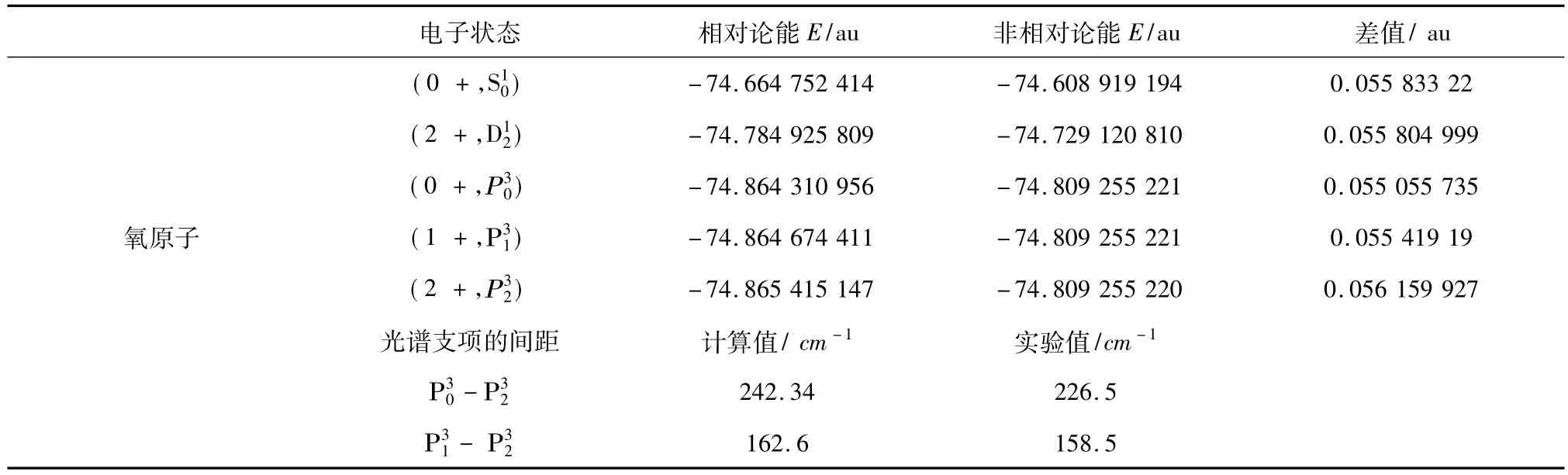
表1 O原子的质量的相对论效应Table 1 The relativistic effect of atomic mass for atoms O

表2 S原子的质量的相对论效应Table 2 The relativistic effect of atomic mass for atoms S

表3 Se原子的质量的相对论效应Table 3 The relativistic effect of atomic mass for atoms Se

为了比较同周期而不同族的原子的质量的相对论效应，计算了C原子，见表4。其中电子状态分别表示相对论的和非相对论的。已知碳原子基电子组态为1s22s22p2，其非相对论的LS偶合得到轨道角动量分别为 s和 d和 p的电子状态为和，而，其中 S和D状只有一个光谱支项，而P状有三个光谱支项，都满足洪特第二规律。所计算的光谱支项的能量的差，都与实验值比较相合。

相对论的和非相对论的能量的差，对于O原子为0.0558到0.0561;对于 C 原子为 0.01205到 0.01218.两者的相对差约为 4.62∶1。

在表5中列出了同族而不同周期的重原子钐和钚的质量的相对论效应。与表1比较，相对论的和非相对论的能量的差，对于O原子为0.0558到0.0561;对于 S 原子为0.9754 到0.9764;对于 Se原子为 26.771到 26.777;对于 Sm 原子为379.054;对于Pu原子为2580.67。如果以 O原子的能量的差为1，则S、Se、Sm 和Pu原子分别为17.5、479、6781和46166。可以看出，就钚和氧比，质量的相对论效应增加46166倍。对于Pu，相对论的和非相对论的能量的差占总能量的 0.0872，即8.72%。所以，对重元素，应用相对论的计算是很必要的。

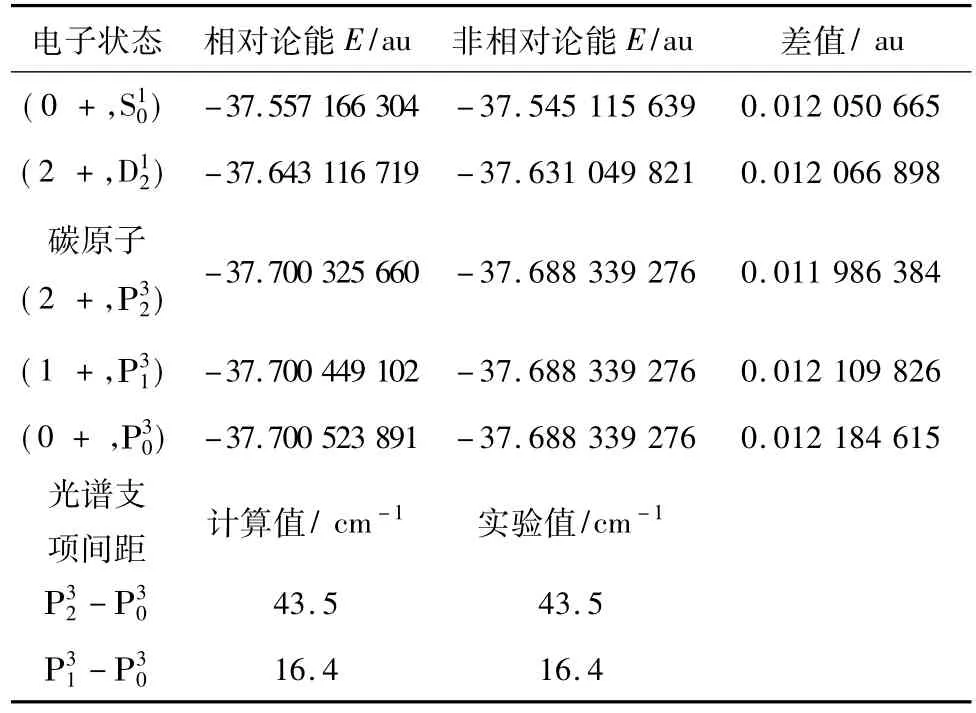
表4 C原子的质量的相对论效应Table 4 The relativistic effect of atomic mass for carbon

表5 重原子钐和钚的质量的相对论效应Table 5 The relativistic effect of atomic mass for Samarium and Plutonium

4 结语

1)比较相对论和非相对论的光谱项和光谱支项可以看出。以碳原子和氧原子为例，非相对论只能给出光谱项Ρ3，而不能给出光谱支项，更谈不上光谱支项的间距。对光谱支项的能级顺序也是不同的，如碳原子为，其能级顺序为对碳原子为和;氧原子为，的能级顺序正好相反，即为和。在实验上，这些都由洪特第一规则和洪特第二规则所确定。然而，由相对论效就自然给出了，并且计算的光谱支项的能量的差，都与实验值比较相合。

2)质量的相对论效应是一种重要的相对论效应，它与系统的能级、光谱结构和电子状态表述等有关。正如钱学森院士所指出，要从认识客观世界转向改造客观世界，提倡“从理论力学转向应用力学”和“从原子与分子物理转向原子与分子工程 ”［7］。基于相对论效应的重要性，需要发展相对论工程，即是说对重元素，要开展相对论量子力学研究和应用。

［1］Lu Ding，W Falter C .Symmetries in Physics［M］.Heidelberg Berlin:Springer－ Verlag，1996.

［2］朱正和.原子分子反应静力学［M］.北京:科学出版社，2007.

［3］Cornwell J F.Group Theory in Physics［M］.London:Academic Press，1994.

［4］Saue T，Jensen H J Aa.Quatermion symmetry in relativistic moleculav calculations:The Dirac－Hartree－Fock method［J］.Chem Phys，1999，111:6211 －6222.

［5］Grant I P，McKenzie B J.The transverse electron － electron interaction in atomic structure calculations［J］.J Phys B，1980，13:2671－2681.

［6］Dyall K G.A general purpose relativistic atomic structure program［J］.Comput Phys Commun，1989，55:425 －456.

［7］朱正和.学习和继承钱森思想［J］.原子与分子物理学报，2009，26(6):988.

The relativistic effect and application of atomic mass

Zhu Zhenghe1，Fu Yibei2，Meng Daqiao2，Tang Yongjian2

(1.Institute of Atomic and Molecular Physics，Sichuan University，Chengdu 610065，China;2.China Academy of Engineering Physics，Mianyang，Sichuan 621900，China)

The present work devotes to the calculation of relativistic and non-relativistic electronic state and energy for atoms C，O，S，Se，Te，Sm and Pu.In comparison between the relativistic and non-relativistic electronic energy，it is concluded that if energy difference of relativistic and non-relativistic electronic energy for O atom is supposed as unit，then there will be 17.5，479，6781 and 46166 for S，Se，Sm and Pu ，respectively.The energy difference of relativistic and non-relativistic electronic energy for Pu is about 8.72%of its total energy.Therefore，it is quite necessary to calculate heavy atoms using relativistic theory.

Dirac theory;relativistic effect of atomic mass;samarium and plutonium

O056

A

1009－1742(2011)01－0021－04

2009－12－20

朱正和(1932―)，男，湖北监利县人，四川大学原子分子物理所教授，博士生导师，研究方向为原子分子物理，E－mail:zhuxm@scu.edu.cn;傅依备(1929―)，男，湖南岳阳县人，中国工程院院士，主要研究方向为核科学技术，E－mail:fuyb@cieb.ac.cn