只测视线角速度的目标可观性判据
2011-03-15田宏亮梁晓庚贾晓洪郭晓楠
田宏亮 梁晓庚 贾晓洪 郭晓楠
(中航工业空空导弹研究院,洛阳 471009)
只测视线角速度的目标可观性判据
田宏亮 梁晓庚 贾晓洪 郭晓楠
(中航工业空空导弹研究院,洛阳 471009)
在二维平面内,把已有的只测视线角的目标可观判据扩展到只测视线角速度的情况.针对N阶机动目标,在直角坐标系中,通过分析导弹与目标相对运动方程,给出了只有视线角速度量测值情况下目标不可观的充分必要条件(目标不可观判据).目标不可观判据分为两种简单的表达形式:一种是对弹目相对距离的约束;另一种是对视线角的约束.在修正极坐标系中,通过分析系统的Fisher信息阵,得到了在只有视线角速度量测值情况下常加速度目标可观的充分必要条件.结果表明:目标不可观判据与在修正极坐标系中得到的充分必要条件是一致的,与只测视线角的目标可观判据不冲突;推理简单,不要求分析可观性矩阵和非线性微分方程,因此简单易用.
制导与控制;可观性;目标运动;加速度;角速度
纯方位角情况下分析目标运动参数估计的可行性(即目标可观性)的研究已经很广泛[1-4],但在只有视线角速度量测值的情况下分析目标可观性的研究却很少.其原因之一是,后者的系统无法精确线性化,并且视线角速度量测值与目标运动参数的关系式较复杂.
红外成像导引头通常只能提供满足精度要求的视线角速度信息,因此研究这种情况下目标可观性判据很有必要.文献[5]基于近似线性化方法和一些假定得出以下结论:测量导弹与目标的视线角速度和测量导弹与目标的视线角相比,可增加系统的可观性;沿着视线方向的目标机动通过测量视线角或视线角速度是不可观测的.但文献[5]没有给出只有视线角速度量测值情况下目标可观测的充分必要条件.
对N阶机动目标,本文直接对导弹与目标相对运动的基本关系式进行研究,推理出只有视线角速度量测值情况下目标不可观测的充分必要条件(即目标不可观判据);根据文献[6]的方法,通过分析系统的Fisher信息阵,研究了常加速度目标在只有视线角速度量测值情况下的可观性,得到的结果符合本文给出的目标不可观判据.
1 导弹与目标的相对运动模型
目标和导弹的轨迹在直角坐标系分别用二维函数 m(t)和 d(t)表示,r(t)和分别表示弹目相对距离和弹目相对速度,β(t)和分别表示弹目视线角和弹目视线角速度,如图1所示.显然有r(t)=m(t)-d(t),这里假设‖r(t)‖不为0.

图1 导弹和目标运动状态示意图
在导弹攻击目标的时间段[0,tf]内,假设目标机动可表示为一个N阶动态模型,表达式为

其中,z=[1 t t2… tN];M为2×(N+1)的未知系数矩阵.
假设导弹的运动轨迹已知,并且可以表示为
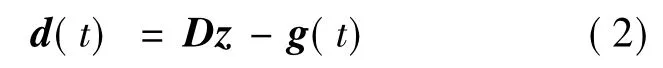
其中,g(t)=[gX(t) gY(t)]为导弹的“机动”;D为2×(N+1)矩阵.
假设g(t)满足:

其中,i={X,Y};k={0,1,…,N}.
由式(1)和式(2)可得

其中,R=M-D为弹目相对运动N阶动态系数矩阵.目标轨迹估计就是估计矩阵R的相关信息.
弹目相对方位关系式为
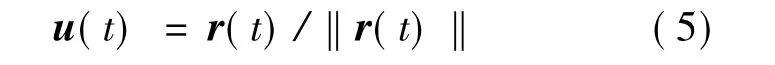
式(5)几何含义为
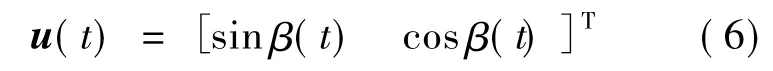
r(t)与u(t)的关系式为
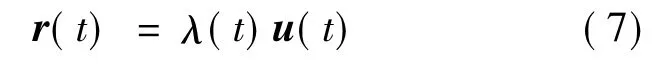
其中,λ(t)为正值函数标量.
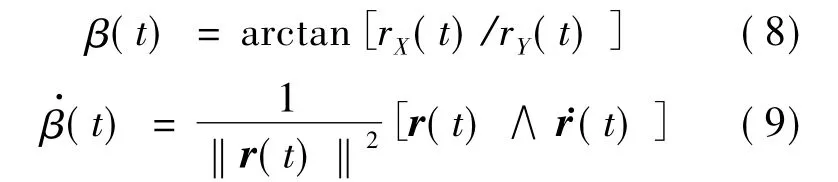
这里定义集合 E,E={χ={r(t),rX(t),λ(t)}:χ同时满足式(3)、式(4)和式(6) ~ 式(9)}.
2 目标不可观判据的推理
定理1只有视线角速度测量值的目标不可观判据 1 .设 χ1和 χ2∈E,如果 g1(t)=g2(t),,则存在 r1(t)≠r2(t)的充分必要条件为

其中,θ为任意常数;α(t)为任意实函数标量;Q为2×(N+1)系数矩阵.
下面根据文献[7]的方法给出定理1的证明.
2.1 定理1必要条件的证明
证明已知 χ1和 χ2∈E,g1(t)=g2(t),等价于 β2(t)=β1(t)+θ.r1(t)和 r2(t)的方向矢量转换关系为
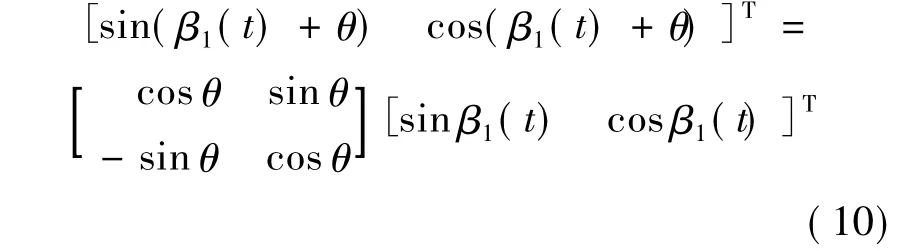
根据式(7)可得

由式(6)、式(7)和r1(t)≠r2(t)的条件可推知,所以由式(11)可得
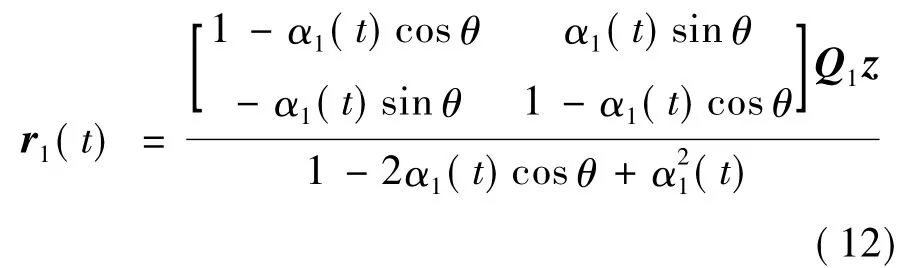
同理可得r2(t)的表达式,与式(12)对比,考虑到β1(t),β2(t)和θ取值的任意性,则结论得证.
证毕
在定理1的必要条件中,如果β2(t)=β1(t)即 θ=0 时,则仍成立,这时定理 1的必要条件与文献[7]对应的必要条件一致.
2.2 定理1充分条件的证明
证明设 χ1和 χ2∈E,{χ1,α1(t),θ1,R1,Q1}满足式(12).令 λ2(t)=α1(t)λ1(t),可得

定义r2(t),使其满足:
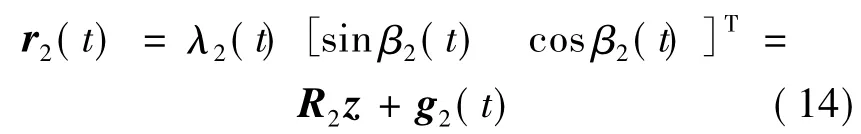
易知r1(t)≠r2(t).根据式(3)可得
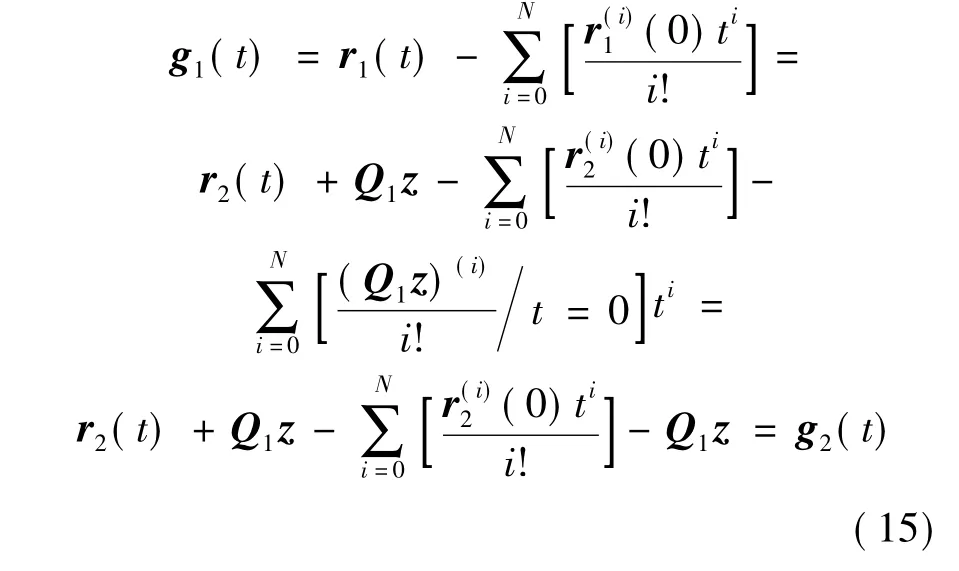
证毕
推理1只有视线角速度测量值的目标不可观判据 2.设 χ1和 χ2∈E,如果 g1(t)=g2(t),,则存在 r1(t)≠r2(t)的充分必要条件为
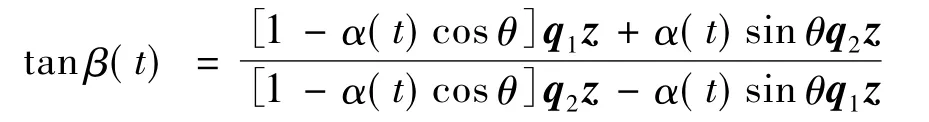
其中,θ为任意常数;α(t)为任意实函数标量;Q为2 ×(N+1)的系数矩阵,Q=[q1q2]T.
证明略.
定理1和推理1对比文献[7]知:目标运动状态在只测视线角情况下可观测时,在只测视线角速度情况下未必可观测;在只测视线角情况下不可观测时,在只测视线角速度情况下必不可观测.但这并不意味前者在目标运动状态可观性方面一定优于后者,因为在系统有干扰时估计参数还和滤波器的性能有关[5].下面针对Fisher信息矩阵的特性进行目标运动状态可观性分析.
3 基于信息阵的目标可观性分析
3.1 弹目运动状态离散测量方程
在修正极坐标系(MPC)[8]中增加目标加速度分量得到向量φ,表达式为
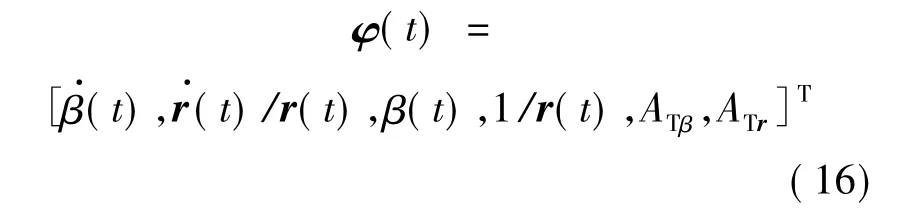
其中,ATβ为目标加速度垂直于弹目视线的分量;ATr为目标加速度沿着弹目视线的分量.设目标加速度是常值.
令下式成立:

其中,aOX(t),aOY(t),aTX(t)和 aTY(t)分别为导弹加速度和目标加速度在X轴和Y轴上的分量.
在MPC中,弹目运动信息离散测量方程是线性的,表达式为

其中,ε(ti)为均值为0和方差为σ2的高斯白噪声;φ1(ti)的精确解表达式为

3.2 目标运动状态可观性分析
Fisher信息矩阵J(tn,t0)用来判断在任意时刻t0∈[0,tf),通过测量值y(ti)观测状态变量φ(t0)的可能性,J(tn,t0)可以简化为
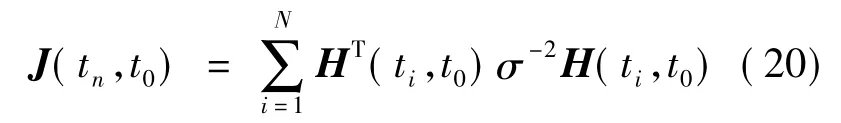
其中,i=1,2,…,n,n≥6;H(ti,t0)为 1 ×6 行向量,表达式为

因为在量测方程式(18)中,ti的值是任意的,所以可以用 t代替 ti.根据一组量测值 y(t1),y(t2),…,y(tn)(n≥6)可以使式(16)和式(18)对应的系统可观测的充分必要条件是:对任意一个6×1非零常数向量μ,都能找到某个时刻t∈(t0,tf],使 H(t,t0)μ≠0 成立[9].限于篇幅,下面只给出H(t,t0)的第4个分量的表达式为

当导弹和目标都匀速运动时,S1W(t,t0),S2W(t,t0),S3W(t,t0) 和 S4W(t,t0) 都为 0,由式(22)知这时φ4(t0)不可观测,与定理1相符.
4 结论
针对N阶机动目标,本文给出了只有视线角速度量测值情况下目标不可观测的充分必要条件(即目标不可观判据),这一条件表明欲保证目标状态可观测,必须根据定理1设计导弹的弹道.针对常加速度目标,通过分析系统的Fisher信息阵,本文研究了只有视线角速度量测值情况下目标的可观性,得到的结果符合本文给出的目标不可观判据.因而本文给出的不可观判据,对利用红外导引头量测值获得目标运动状态估计的工作,在理论和实际应用上都有意义.
References)
[1] Nardone SC,Aidala V J.Observability criteria for bearings-only target motion analysis[J].IEEE Transactions on Aerospace and Electronic Systems,1981,AES-17(2):162 -166
[2] Hammel SE,Aidala V J.Observability requirements for three-dimensional tracking via angle Measurements[J].IEEE Transactions on Aerospace and Electronic Systems,1985,AES-21(2):200-207
[3]杨国胜,窦丽华,侯朝桢.基于纯角度的三维运动目标可观性研究[J].兵工学报,2004,25(2):182 -185 Yang Guosheng,Dou Lihua,Hou Chaozhen.Observability criteria based on bearing-only measurments for three-dimensional moving targets[J].Acta Armamentarii,2004,25(2):182 - 185(in Chinese)
[4]刘健,刘忠,玄兆林.方位时延的TMA算法及其可观测性研究[J].声学技术,2007,26(3):371 -375 Liu Jian,Liu Zhong,Xuan Zhaolin.Bearing and time delay measurement using TMA algorithm and its observability[J].Technical Acoustics,2007,26(3):371 -375(in Chinese)
[5] Hepner SA R,Geering H P.Observability analysis for target maneuver estimation via bearing-only and bearing-rate-only measurements[J].Journal of Guidance,Control and Dynamics,1990,13(6):977-983
[6] Song T L,Um T Y .Practical guidance for homing missiles with bearings-only measurements[J].IEEE Transactions on Aerospace and Electronic Sytems,1996,32(1):434 -442
[7] Fogel E,Gavish M.N th-order dynamics targetobserv-ability from angle measurements[J].IEEE Transactions on Aerospace and Electronic Systems,1988,24(3):305 - 308
[8] Aidala V J,Hammel SE.Utilization ofmodified polar coordinates for bearings-only tracking[J].IEEE Transaction on Automatic Control,1983,AC-28:283 -294
[9] Song T L.Observability of target tracking with range-only measurements[J].IEEE Journal of Oceanic Engineering,1999,24(3):383-387
(编 辑:刘登敏)
Target observability criteria from bearing-rate-only measurements
Tian Hongliang Liang Xiaogeng Jia Xiaohong Guo Xiaonan
(AVIC Airborne Missile Academy,Luoyang 471009,China)
Target observability criteria previously established for bearing-only tracking in two dimensions was extended to that for bearing-rate-only tracking.For unobservability of N th-order dynamics target from bearing-rate-only measurements,by an analysis of the relative movement equation of missile and target,the necessary and sufficient conditions(target unobservability criteria)were presented in Cartesian coordinates.The unobservability criteria has two simple forms,one is the restriction of relative distance of missile and target,and the other is the restriction of line-of-sight angle.For observability of constant acceleration target from bearing-rate-only measurements,by an analysis of the system fisher information matrix,the necessary and sufficient conditions were obtained in modified polar coordinates.Result shows that the target unobservability criteria is identical with the necessary and sufficient conditions established in modified polar coordinates,and is consistent with the target observability criteria for bearing-only tracking,besides which,is derived easily without examination of an observability matrix and nonlinear differential equations,which fits it for appliance.
guidance and control;observability;objectmotion;acceleration;angle rate
V 448.133
A
1001-5965(2011)05-0534-04
2010-01-27
田宏亮(1972-),男,河南鹤壁人,博士生,thlnhy666@163.com.
