基于随机鲁棒分析的输出反馈特征结构配置

金宪哲 吴森堂

(北京航空航天大学 自动化科学与电气工程学院,北京 100191)

基于随机鲁棒分析的输出反馈特征结构配置

金宪哲 吴森堂

(北京航空航天大学 自动化科学与电气工程学院,北京 100191)

针对输出反馈特征结构配置在参数不确定性系统设计中的鲁棒性问题,提出一种基于随机鲁棒分析的输出反馈特征结构配置优化方法.该方法通过随机鲁棒分析准确度量了闭环系统的鲁棒性,确立控制系统设计要求与待设计参数间的直接联系,并运用优化技术实现闭环系统稳定性与性能间的折衷,最大化控制系统的鲁棒性.通过在某高超声速飞行器横侧向解耦控制系统设计上的应用,验证了该方法的有效性.

特征结构配置;随机鲁棒分析;鲁棒控制;反馈控制

特征结构配置(EA,Eigenstructure Assignment)是一种通过极点配置,使闭环特征值及其相应的特征向量满足指定的设计要求,以获得期望的闭环系统响应的现代控制设计方法,其广泛应用在飞行控制系统的静态解耦设计上[1-3].由于实际系统中不是所有状态都是可测的,当采用输出反馈特征结构配置时,因系统信息的缺失,在设计过程中无法获知未配置特征值的变化情况,设计结果可能导致系统是不稳定的.同时,外界干扰等因素引起的参数不确定性也会影响闭环系统的稳定性.另外,运用 EA设计出的定常增益输出反馈矩阵能否使系统的特征结构在整个不确定性参数变化范围内满足设计要求,也是需要重点关注的问题,这在进行解耦控制设计时尤为重要.目前,鲁棒特征结构配置已经取得了许多研究成果[3-7],但在系统参数不确定性信息的利用、鲁棒性优化以及工程实用性等方面仍需要更进一步的探讨.

鲁棒控制的重要元素之一是分析控制系统鲁棒性的技术,本文中引入随机鲁棒分析[8-9](SRA,Stochastic Robustness Analysis)对控制系统的鲁棒性进行度量.SRA是一种用于评估线性时不变系统鲁棒性的数值方法,通过对闭环系统特征值以及性能的蒙特卡罗估计,获得不确定性参数统计意义下的闭环系统不稳定概率和性能不满足概率,作为闭环系统的鲁棒稳定性度量和鲁棒性能度量.使用不稳定概率和性能不满足概率量化系统鲁棒性的一个优点是:它能够明确地指出系统可允许多大的参数不确定性而不失鲁棒性.SRA中二项置信区间的应用保证了鲁棒性度量的精确性.

本文针对输出反馈特征结构配置在参数不确定性系统设计中的鲁棒控制问题,提出一种基于SRA的特征结构配置方法——SRA-EA.SRA-EA在设计过程中充分考虑了设计要求以及系统参数不确定性的信息,同时兼顾特征值及相应特征向量的变化情况,最大化地实现了控制系统的鲁棒性.

1 特征结构配置

考虑线性时不变系统:

式中,x∈Rn,u∈ Rm,y∈ Rr和 q∈Rl分别为系统的状态向量、输入向量、输出向量和系统参数向量;A(q),B(q)和 C(q)分别为系统矩阵、输入矩阵和输出矩阵,它们是关于系统参数向量 q的任意函数.假设 q有已知的或估计的概率密度函数f(q),统计地描述了系统的参数不确定性.

对某一确定的 q0,采用输出反馈

进行特征结构配置,K∈Rm×r为增益输出反馈矩阵,闭环特征值 λi(i=1,2,…,r)与相应的特征向量 vi(i=1,2,…,r)有如下关系:

式中,I为单位矩阵.由于缺少足够的系统信息,输出反馈特征结构配置一般无法将 vi精确配置到期望的特征向量,实际得到的特征向量只是一种最可能的结果,它是由(λiI-A(q0))-1·B(q0)的列所张成子空间上的投影.有关的计算在文献[10]中有详细描述.

为便于计算,通过线性变换 x=Tx～,其中

Q为使 rank(T)=n的任意矩阵,将原系统

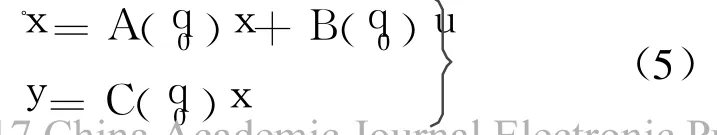
变换为

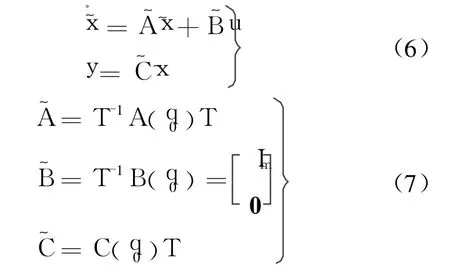
原系统的特征值与变换后系统的特征值一致,而相应的特征向量之间有如下关系:

由文献[10],有

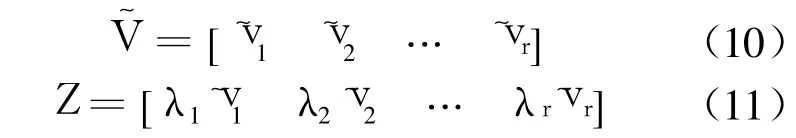
根据以上算法得到的 K,虽能够精确配置闭环系统的 r个特征值,但缺少其余 n-r个特征值的信息而无法确定闭环系统是稳定的.这种情况在系统存在参数不确定性,即 q按 f(q)指定的规律变化时,会变得更为复杂,因为 K只是在 q0的条件下得到的.此外,闭环系统特征向量也会因参数不确定性而偏离期望特征向量,闭环系统可能无法达到期望的性能.

2 SRA-EA

针对上述问题,本文在输出反馈特征结构配置过程中,运用 SRA设计对控制系统的鲁棒稳定性和鲁棒性能进行分析,并在此基础上对 K进行寻优,最大化闭环系统的鲁棒性.

2.1 待设计参数向量的选取

若确定了特征向量各元素的构成形式,期望闭环特征值与 K之间存在着某种映射关系.这里将需要配置的闭环特征值 λi(i=1,2,…,r)作为待设计参数向量 h,h∈Rr,即

期望闭环特征值的可允许变化范围构成了 h的设计参数空间.

K可根据 h和标称系统由上述算法得到.一般地,将 q变化范围内的 A(q)、B(q)和 C(q)的均值所构成的系统设为标称系统.

2.2 鲁棒稳定性度量

对于某一确定的 K,若输出反馈配置的闭环特征值 λi(i=1,2,…,r)在整个参数不确定性变化范围内满足设计要求,同时,未配置的特征值λi(i=r+1,r+2,…,n-r)均具有负实部,则认为控制系统是鲁棒稳定的.

由于每次关于稳定性的蒙特卡罗估计只会产生两种结果:稳定或不稳定,因此,每次的蒙特卡罗估计可用二项随机变量 X1表示.若闭环系统在一次蒙特卡罗估计中是鲁棒稳定的,则令 X1=0;否则,X1=1.闭环系统的不稳定概率估值可近似为[9]

式中,J为蒙特卡罗估计次数.J越大,p1越接近真实的不稳定概率.

2.3 鲁棒性能度量

若将闭环系统的性能指标转化成二项决策(binomial decision)的形式,就可用类似地的方法得到闭环系统的性能不满足概率估值,以描述控制系统的鲁棒性能.一般地,系统的性能很难仅用一个指标描述其优劣,常用的性能指标有调节时间、超调量以及特定应用要求(如解耦设计中特征结构所要满足的条件)等.控制系统的鲁棒性能由各项鲁棒性能度量综合描述.

本文采用确定的性能可接受边界作为此项性能的判据,若闭环系统的某项性能在可接受边界内,则相应的二项随机变量 Xi=0(i≥2);否则,Xi=1.因此,闭环系统该项指标的性能不满足概率估值为

2.4 二项置信区间的应用

由于 pi都是估计值,它接近真实不稳定概率或性能不满足概率 p-i的精度需要通过二项置信区间来保证.

由文献[9]可知,关于不稳定概率(或性能不满足概率)P的置信水平为 1-α的置信区间为

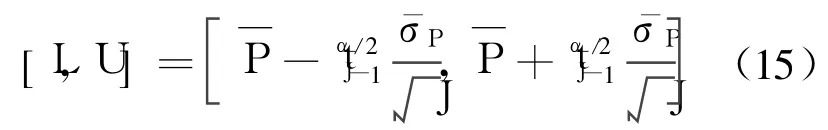
文献[9]还同时给出了在给定准确性系数 ε和置信系数 α情况下所需最少的 J,从而解决了蒙特卡罗估计内在的计算问题.

判断待设计参数向量 h1所对应的控制系统是否比 h2所对应的控制系统更加鲁棒,可通过计算它们的不稳定概率或性能不满足概率之差来确定.设 P1为 h1所对应不稳定概率或性能不满足概率,P2为 h2所对应不稳定概率或性能不满足概率,并假设 P1＞P2,则两个概率之差 ΔP≜P1-P2的置信区间可根据 P1和 P2的独立置信区间给出[8]:

ΔP的置信区间可由下式给出:

若 ΔP的置信区间包含了 0,说明两个控制系统在各自的估计次数和置信系数情况下,鲁棒性上没有显著差异,即认为两个控制系统具有相同的鲁棒稳定性或鲁棒性能;否则,概率越小的控制系统其鲁棒性越强.

2.5 鲁棒性优化设计

鲁棒特征结构配置的目的是设计常值反馈矩阵,使闭环系统的特征值及相应特征向量中指定元素不会因系统参数不确定性的影响而超出设计要求,从而保证系统的鲁棒稳定性和鲁棒性能.

因此,鲁棒特征结构配置的问题可以描述为:在 h的设计参数空间内寻找 h*,使得不稳定概率以及各项性能不满足概率最小.但是,鲁棒控制系统设计的一个不可避免的问题是,系统的鲁棒稳定性与某些性能指标之间存在着某种折衷,对于此类折衷问题,可应用优化技术实现.

设优化代价函数为

式中,M为关注的控制系统设计指标的个数;pi为各项设计指标的不满足概率;wi为 pi的加权,通过调整 wi可实现稳定性与各项性能指标间的折衷.

判断是否成功实现鲁棒特征结构配置设计,取决于待解决的实际问题.一般只要满足下列条件之一即可:

1)pi最小;

2)在满足可靠性要求的前提下,pi足够小.

若获得的 h*无法满足设计要求,则可以根据pi的值修改相应的设计指标,或改变 h的设计空间范围,重新进行设计.

3 设计算例

某高超声速飞行器横侧向非线性状态方程为

式中,β,φ,p,r,δa,δr分别为侧滑角、滚转角 、滚转角速度、偏航角速度、升降副翼偏角和方向舵偏角 ;T,Y,α,θ,q,m,V分别为推力、侧力 、迎角 、俯仰角、俯仰角速度、质量和飞行速度;Iz分别为滚转力矩、偏航力矩以及飞行器各轴的转动惯量;Gya为重力在气流坐标系 y轴上的投影;以上各参数遵循英美坐标系定义.Tδa,kδa,Tδr,kδr分别为升降副翼和方向舵的时间常数和增益;δac,δrc分别为升降副翼偏转指令和方向舵偏转指令.

应用 SRA-EA方法进行横侧向飞行控制系统设计,要求在飞行高度H∈[18000,25000]m,V∈[1700,2400]m/s,质量 m∈ [121000,180000]kg的飞行包线内采用输出反馈特征结构配置实现飞行器荷兰滚模态与滚转模态之间的解耦.输出反馈为 β,φ,p,r.

设 H,V和 m按均匀分布进行摄动,待设计参数向量 h=[λ1λ2λ3λ4]中各元素分别对应闭环荷兰滚模态(β,r)和滚转模态(φ,p).h的设计参数空间为

各模态所对应的期望特征向量为

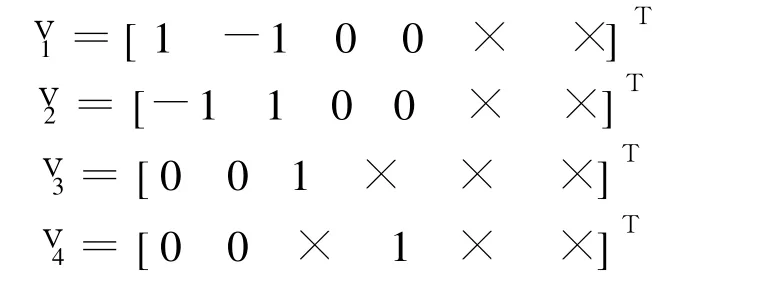
式中,×表示特征向量中未指定的分量.

为实现模态间的解耦,在应用 SRA-EA设计时的性能指标要求:期望闭环特征向量中指定为1或 -1的分量在整个飞行包线内变化量不超过5%,分量为 0的变化不超过 ±0.05.

置信水平取 1-α=0.95,准确性系数 ε=0.0001,可确定 J的最小值为 29955,增加额外的估计次数可进一步提高估计精度,最终设定 J=30000.不稳定概率以及性能不满足概率的期望值均为 1.2×10-3.

不稳定概率的加权 w1=10,性能不满足概率的加权 wi=1(i≥2).

用遗传算法对 h进行寻优,最终得

高超声速飞行器横侧向解耦控制系统在初始条件为 β=1°时的非线性随机时间响应曲线如图1所示.

图 1 初始条件为 β=1°时的非线性随机响应

初始条件为 φ=20°时的非线性随机时间响应曲线如图 2所示.

图 2 初始条件为 φ=20°时的非线性随机响应

仿真结果表明:所设计的控制系统能够在给定的飞行包线内实现荷兰滚模态与滚转模态间的解耦.

4 结 论

SRA-EA有效解决输出反馈特征结构配置在参数不确定性系统设计中存在的鲁棒性问题.该方法充分利用了系统参数不确定性信息,设计结果对控制系统鲁棒性的影响以及各设计指标间的折衷直接体现在设计中,便于设计人员了解和改进设计过程,有效避免产生过度保守的设计,具有较高的工程实用价值.

References)

[1]刘小刚,吴梅,安锦文.基于特征结构配置/定量反馈理论的飞行控制系统设计研究[J].弹箭与制导学报,2006,26(1):340-343 Liu Xiaogang,Wu Mei,An Jinwen.Application of EA based QFT in design of lateral flight control system[J].Journal of Projectiles,Rockets,Missiles and Guidance,2006,26(1):340-343(in Chinese)

[2]李帆,周凤岐,周军.导弹基于特征结构配置的输出反馈解耦控制[J].弹箭与制导学报,2001,21(3):5-8 Li Fan,Zhou Fengqi,Zhou Jun.Decoupling control of missile by output feedback eigenstructure assignment[J].Journal of Projectiles,Rockets,Missiles and Guidance,2001,21(3):5-8(in Chinese)

[3]Seo Young Bong,Choi JaeWeon.Eigenstructure assignment considering probability of instability with flight control application[J].International Journal of Control,Automation,and Systems,2007,5(6):607-613

[4]王德军,李元春.线性系统的鲁棒特征结构配置[J].吉林大学学报:信息科学版,2004,22(5):476-480 Wang Dejun,Li Yuanchun.Rob usteig enstru cture assign-ment for a class of linear systems[J].Journal of Jilin University:Information Science Edition,2004,22(5):476-480(in Chinese)

[5]潘常春,陈欣.基于鲁棒特征结构配置的无人机直接侧力控制[J].飞行力学,2004,22(3):84-87 Pan Changchun,Chen Xin.UAV direct side force controllaw design with robust eigenstructure assignment[J].Flight Dynamics,2004,22(3):84-87(in Chinese)

[6]黄玲,段广仁,于海华.广义二阶动力学系统的鲁棒特征结构配置[J].控制理论与应用,2009,26(3):238-242 Huang Ling,Duan Guangren,Yu Haihua.Robust eigen structure assignment in descriptor second-order linear systems[J].Control Theory＆Application,2009,26(3):238-242(in Chinese)

[7]Seo Young Bong,Choi Jae Weon,Man Hyung Lee.Eigen structure assignment for LTI systems with stochastic parameter variations[C]//Proceedings of the 2000 American Control Conference.Chicago:ACC,2000:3812-3816

[8]Ryan Laura Ray.Stochastic robustness of linear multivariable control systems:towards comprehens-ive robustness analysis[D].Princeton:Department of Mechanical and Aerospace Engineering,Princeton University,1991

[9]吴森堂.飞航导弹制导控制系统随机鲁棒分析与设计[M].北京:国防工业出版社,2010:8-23 Wu Sentang.Stochastic robustness analysis and design for guidance and control system of winged missile[M].Beijing:National Defense Industry Press,2010:8-23(in Chinese)

[10]Stevens Brian L,Lewis Frank L.Aircraft control and simulation[M].New York:Wiley,1992:347-353

(编 辑:刘登敏)

Output feedback eigen structure as signment based on stochastic robustness analysis

Jin Xianzhe Wu Sentang

(School of Automation Science and Electrical Engineering,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)

An approach for output feedback eigenstructure assignment(EA)of linear multi variable system with parameter uncertainty was presented based on stochastic robustness analysis(SRA),which was used to solve the problem of the eigen structure robustness.With SRA,the robustness measures of closed-loop control system could be achieved accurately.And the direct relationship between the control system design specifications and the design parameters was established.The optimization algorithm was employed to maximize the control system robustness through trading off bet ween the stability and the performances.At last,SRA-EA was applied to the decoupled design for lateral control system of the hypersonic vehicle.The numerical simulations demonstrated the effectiveness of the presented approach.

eigenstructure assignment;robustness;robust control;feedback control

TP 13

A

1001-5965(2011)04-0487-05

2010-10-19

十一五国防基础科研资助项目(A 212006×××)

金宪哲 (1973-),男,黑龙江佳木斯人,博士生,jinxianzhe_first@sina.com.