基于空间解析几何关系的焦点投影位置测量

李 斌 傅 健 周正干

(北京航空航天大学 机械工程及自动化学院,北京 100191)

基于空间解析几何关系的焦点投影位置测量

李 斌 傅 健 周正干

(北京航空航天大学 机械工程及自动化学院,北京 100191)

为了抑制工业计算机层析成像(CT,Computed Tomography)过程中的重建伪影,研究了一种基于空间解析几何关系的射线源焦点投影位置测量方法,并完成了计算机仿真和实验验证.该方法根据工业 CT扫描系统的几何结构关系建立射线源焦点投影位置和转台旋转中心投影位置之间的空间解析表达式,然后通过测量转台旋转中心在多个位置的投影来解析求解射线源焦点投影位置.该方法要求转台具有 3个自由度:旋转,平行于探测器方向移动,和垂直于探测器方向移动.仿真和实验结果表明,该方法能够有效抑制重建伪影.该方法无需使用特殊模体,不需要任何先验几何参数,较现有方法更为方便.

层析成像;无损检测;二维;测量;像质;最小二乘法

工业 CT(Computed Tomography)技术能够在不破坏物体的情况下,通过射线扫描和重建算法,精确的重构物体内部结构信息,在航空、航天、兵器及核工业等领域产品的无损检测中[1]发挥了重要的作用.

在进行工业 CT成像前,需要调整和测量射线源、探测器和转台的相互位置,使其空间几何关系满足标准滤波反投影重建算法的要求:射线源焦点和转台中心的连线须垂直于探测器.准确定位射线源焦点在 X射线探测器上的投影位置是测量和调整这一空间几何关系的前提.不正确的射线源焦点投影位置将在 CT图像中引入重建伪影.现有的焦点投影位置测量与校准方法主要分为 4类:直接测量法[2],单质点估计法[3-4],多质点估计法[5]和解析法[6-7].直接测量法是利用一种特殊的装置直接测量焦点投影位置,例如制作由纸片和铅片交错重叠的夹心面包板.单质点估计法以单个质点在若干个视角下测得的投影坐标值去估计 CT系统的几何参数.由于理想的质点无法实现,通常用小球或钨丝等成像,通过图像处理方法提取其投影质心,来近似当作一质点的投影.然后按照某种误差最小原则,利用迭代方法去估计系统几何参数.多质点估计法和单质点估计法的基本思想类似,不同的是在测量实际投影坐标时,将单个质点变为多个质点,利用多个质点之间预先已知的位置关系,按照某种误差最小原则,利用迭代方法估计系统几何参数.单质点估计和多质点估计方法均属于最优化问题的求解,需接近真实值的初始解,否则容易产生病态解.解析法利用解析表达式求解系统几何参数,不会产生病态解,但通常需要一个与算法对应的特定模体.

针对现有方法的局限性,本文研究了一种基于空间解析几何关系的扇束工业 CT射线源焦点投影位置测量方法,该方法属于解析法范畴,但其不需要制作特定的模体,无需任何先验几何信息.

1 扇束工业 CT扫描结构

图 1显示了扇束工业 CT的扫描结构.被检物固定在转台上随转台一起旋转 360°,即完成一次 CT扫描.

CT重建算法要求射线源和旋转中心的连线必须垂直于探测器,即要求 sx和 cx重合,如图 1a所示.但在工程实际中仅靠机械调整难以使 sx和cx重合,从而在图像重建中引入伪影,如图 1b所示.为使 sx和 cx重合,可以通过精确测量 sx,并移动转台位置,改变 cx,使其等于 sx,即将图 1b的扫描结构校正为图 1a所示.

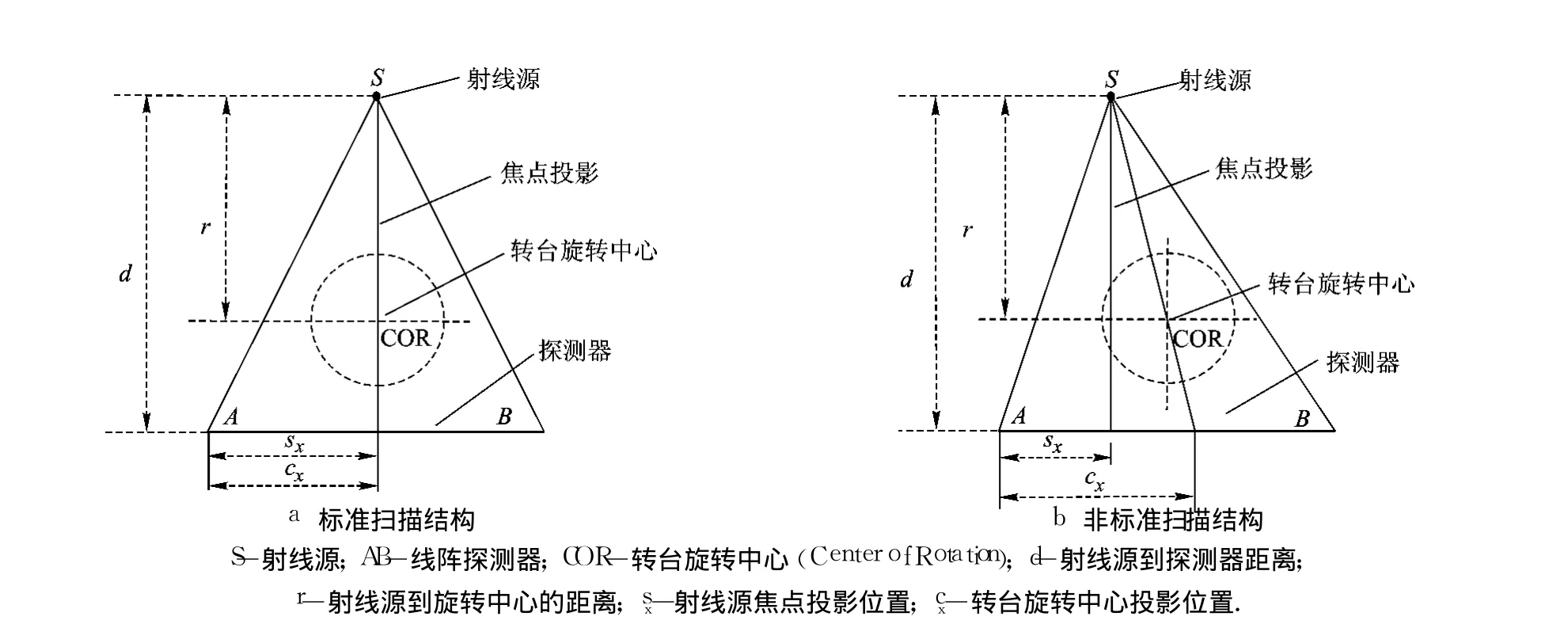
图1 扇束工业CT扫描结构图

2 基于空间几何关系的 sx测量方法

基于图 1所示扫描结构的空间解析几何关系,本文研究了 sx的测量方法,原理如图 2所示.首先,分析扇束工业 CT扫描几何结构,建立 sx与cx之间的解析表达式;然后,将转台旋转中心看作空间一质点,利用文献[8]中的方法测量该质点在空间不同位置的投影位置 cx;最后,利用 sx与 cx的解析表达关系,计算出射线源焦点的投影位置sx.

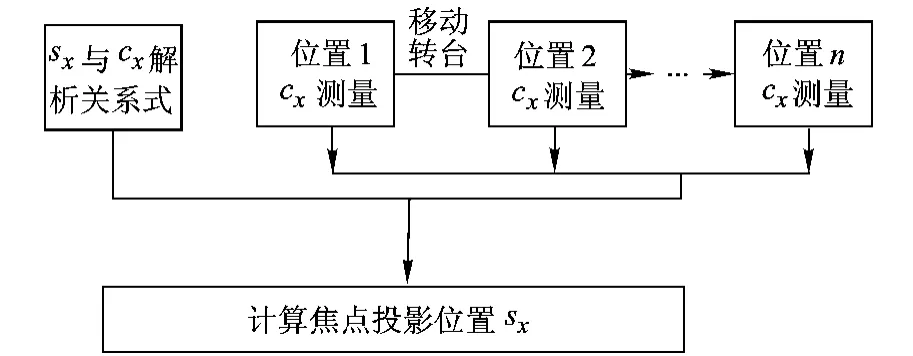
图 2 算法原理图

2.1 sx和 cx的解析关系

如图 3所示,以探测器左端点为坐标原点.将转台旋转中心由 C1点水平移动到 C2点,分别测量转台旋转中心在 C1点和 C2点的投影位置 xc1和 xc2.同理,再移动转台,分别测量转台旋转中心在 C3,C4等点的投影位置.

分析 C1位置的投影几何关系,有

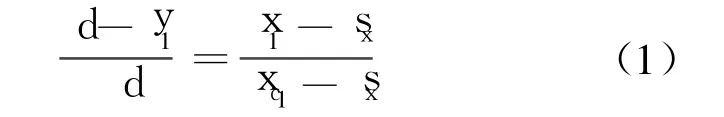
分析 C2位置的投影几何关系,有

图 3 射线源焦点投影位置测量示意图

联立式(2)和式(3)可得

除去转化这一数学的方式外我们在数学问题解答上也需要采用更多的学习方式，学生的思维是各具特色，应对方法也是应该多样。特别是在具有一定操作的实际问题上。例如“平行四边形面积”教学内容中，探索平行四边形面积公式时可以采用多样的数学方式：从不规则图形转化为规则图形上去探究公式、也可以利用教具“四杆机构”来帮助学生研究公式、从特殊的平行四边形（长方形）中推导公式。根据不同的学生采用不同的数学方式。

同理,分析 C3,C4位置的投影几何关系,可得

此时,联立式(4)和式(5),即可求出射线源焦点投影位置 sx:

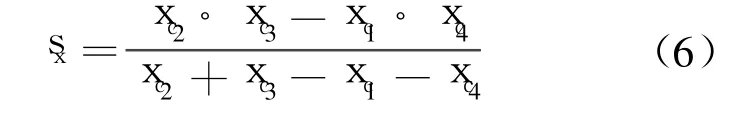
以上表明,进行 4个位置的转台旋转中心投影位置测量,即可解析计算出 CT系统的焦点投影位置.但为了提高结果精度,减小因图像噪声和机械系统定位误差引起的测量误差,可进行更多次的测量.

如图 3所示,设将每次测量的转台旋转中心的位置依次编号为 C1,C2,C3,….

根据式(4),令

其中,x是自变量;y是 x的函数.

则(xc2,xc1),(xc4,xc3),…均是该函数上的点,利用最小二乘法,解得该函数的参数 sx为

2.2 实现步骤

基于 sx和 cx的解析关系式(8),可按如下步骤实现扇束工业 CT扫描结构的校正:

1)将转台旋转中心移动到 C1点,利用文献[8]中的方法计算旋转中心投影位置 xc1;

2)将转台旋转中心移动到 C2点,通过机械系统保证线段 C1C2平行于探测器,利用文献[8]中的方法计算旋转中心投影位置 xc2;

3)如图 4所示,依次移动转台旋转中心到C3,C4,C5,C6等位置,并利用文献[8]中的方法计算旋转中心投影位置 xci,i=3,4,5,…;

4)根据上述测量结果和式(8)计算焦点投影位置 sx;

5)根据焦点投影位置 sx,移动转台,使得转台中心投影位置和焦点投影位置重合,即使得 CT扫描结构如图 1a所示.至此,完成 CT扫描结构的校正.

3 计算机仿真

为验证本文提出方法的正确性与有效性,以Sheep-Logan模型实施 CT成像仿真实验.

仿真条件:射线源到探测器距离 1 200mm,探测器探元大小 127μm,探测器探元个数为 1920,周向采样角度数为 360.采用 8个不同位置的转台旋转中心投影坐标 cx测量焦点的投影位置 sx.图 4给出了计算机仿真的进行 sx校正前后的 CT图像对比.

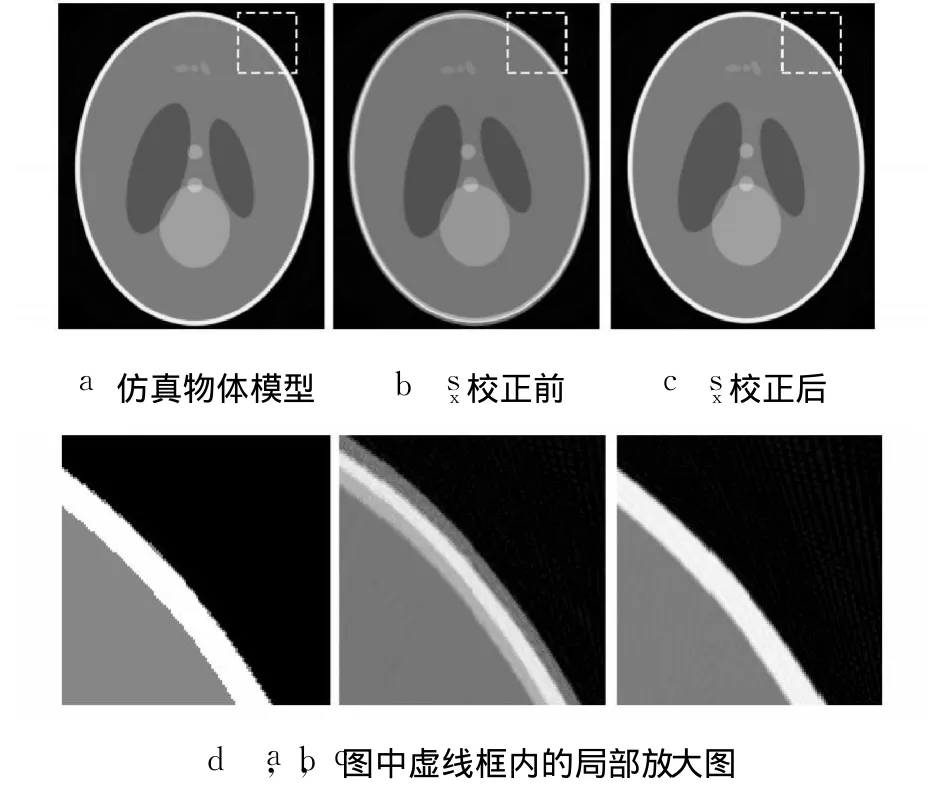
图 4 sx校正前后的 CT图像对比

在仿真过程中,对原始投影数据添加了均值为 0的高斯噪声,表 1给出了 3种噪声水平下的仿真测量结果,其中噪声幅度指噪声标准差和最大投影值的百分比.通过对原始投影数据进行上采样,实现了亚像素级的数据测量.利用计算机模拟重复实验,给出了测量结果的均值和标准差.

仿真结果表明,投影噪声会对实验结果产生一定的影响.当投影数据噪声达到 1%时,sx的测量误差超过了工程允许范围[2].因而,实际测量时,应通过增加采样角度数或者增加单角度下的投影叠加幅数以降低数据噪声.

表 1 sx的仿真测量结果

4 实 验

为验证本文提出方法的正确性与有效性,以某构件为对象实施 CT成像实验.

实验条件:射线源到探测器距离 1200mm,射线源焦点大小 0.2mm(欧洲标准 EN12543),探测器探元大小 0.127mm,探测器探元个数为 1 920,周向采样角度数为 360.管电压 130 kV,管电流2mA.

图 5中,在没有进行 sx测量与校正的系统中获得的 CT图像具有明显的伪影;在进行了 sx测量与校正后,CT图像伪影得到了明显抑制.这也表明了进行焦点投影位置测量与校正的必要性.

图 5 sx校正前后的 CT图像对比

5 结 论

本文提出了一种二维扇束工业 CT系统射线源焦点投影位置的测量方法,无需特殊模体,无需先验几何信息,简单易行.仿真与实验结果表明,该测量方法能满足工程需求,有效抑制 CT重建伪影.

References)

[1]张朝宗,郭志平,张朋,等.工业 CT技术和原理[M].北京:科学出版社,2009:3-10 Zhang Chaozong,Guo Zhiping,Zhang Peng,et al.Technique and principle of industrial CT[M].Beijing:Science Press,2009:3-10(in Chinese)

[2]张全红.X射线工业 CT成像优化研究[D].北京:北京航空航天大学机械工程及自动化学院,2006 Zhang Quanhong.Optimization research on X-ray industrial CT imaging[D].Beijing:Schoolof Mechanical Engineering and Automation,Beijing University of Aeronautics and Astronautics,2006(in Chinese)

[3]Gullberg G T,Tsui B M,Craw ford CR,et al.Estimation of geometrical parameters for fan beam tomography[J].Phys Med Biol,1987,32(12):1581-1594

[4]Gullberg G T,Tsui B M,Craw ford CR,et al.Estimation of geometrical parameters and collimator evaluation for cone beam tomography[J].Med Phys,1990,17(2):264-272

[5]Strubel G,Clackdoyle R,Mennessier C,et al.Analytic calibration of cone-beam scanners[C]//Yu B.2005 IEEE Nuclear Sciences Symposium Conference Record.Fajardo,PR:IEEE,2005:2731-2735

[6]Sun Y i,Hou Ying,Zhao Fengyong,et al.A calibration method for misaligned scanner geometry in cone-beam computed tomography[J].NDT＆E International,2006,39:499-513

[7]Noo F,Clackdoyle R,Mennessier C,et al.Analytic method based on identification of ellipse parameters for scanner calibration in cone-beam tomography[J].Phy Med Biol,2000,45:3489-3508

[8]李保磊,傅健,黄巧珍,等.一种基于正弦图的工业 CT系统转台旋转中心自动确定方法[J].航空学报,2009,30(7):1341-1345 Li Baolei,Fu Jian,Huang Qiaozhen,et al.Automatic calculation of turntable center based on sinograms in industrial CT systems[J].Acta Aeronautica et Astronautica Sinica,2009,30(7):1341-1345(in Chinese)

(编 辑 :张 嵘)

Method for measuring projection position of focal point based on space geometrical relations

Li Bin Fu Jian Zhou Zhenggan

(School of Mechanical Engineering and Automation,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)

In order to reduce artifacts on industrial computed tomography(CT)images,one method for measuring the projection position of the focal point based on space geometrical relations was put forward.Computer simulations and experiments were carried out.The method established analytic equations between the projection position of the focal point and the projection position of the center of rotation.The projection position of the focal point was calculated through several times calculation of the center of rotation in different places.The method required the turntable to have three freedoms:rotating,moving parallel to the detector and moving vertical to the detector.Computers imulations and experiments results demonstrate that this method is effective to reduce CT artifacts.Compared with the current methods,the proposed algorithm need not any special phantoms and need not any priori geometry parameters.It is more convenient for engineering.

computerized tomography;nondestructive examination;two dimensional;measurements;image quality;least squares approximations

TP 391

A

1001-5965(2011)04-0458-04

2010-05-15

国家自然科学基金资助项目(50875013);北京市自然科学基金资助项目(4102036);北京市科技新星计划资助项目(2009A 09)

李 斌(1983-),男,湖北安陆人,博士生,libin@me.buaa.edu.cn.