空间四面体翻滚机器人运动学分析及仿真实验

张利格 毕树生

(北京航空航天大学 机械工程及自动化学院,北京 100191)

彭朝琴

(北京航空航天大学 自动化科学与电气工程学院,北京 100191)

空间四面体翻滚机器人运动学分析及仿真实验

张利格 毕树生

(北京航空航天大学 机械工程及自动化学院,北京 100191)

彭朝琴

(北京航空航天大学 自动化科学与电气工程学院,北京 100191)

对四面体及多面体机器人的研究现状进行了分析.介绍了空间四面体翻滚机器人的结构,由 6根伸缩臂和 4个顶部节点平台组成,通过伸缩臂的运动可以使四面体的重心失稳,实现翻滚运动.结合四面体翻滚机器人的运动形式,给出了翻滚的临界条件,根据不同的运动阶段对四面体翻滚机器人进行了运动学分析.利用 Adams虚拟样机技术对四面体翻滚机器人进行了运动学仿真,并进行了样机的实验,验证了方法的正确性.该分析结果可进一步用于空间四面体翻滚机器人的动力学分析和优化设计.

空间四面体翻滚机器人;运动学分析;临界条件;运动学仿真

空间四面体翻滚机器人的概念最初由 Ham linand和 Sanderson[1-2]等人提出,它是一种变几何桁架机构(VGTM,Variable Geometry Truss Mechanisms),由静定桁架中某些杆件(伸缩杆)的长度可伸缩变化来实现机构的运动,是多自由度多环路的新型机构.伸缩杆的运动可以使四面体的形状发生变化,重心位置随之而变,当超越其稳定区域时,四面体机器人失稳,实现翻滚运动.通过多个四面体单元的组合及拆分可以构成四重四面体乃至十二重四面体等多面体机器人系统.随着机器人重数的增加,机器人的自由度会随之增加,因而能够实现的运动也更为复杂[3-4].

空间四面体翻滚机器人较常规移动机器人具有以下几个优点:①结构上具有对称性和稳定性,四面体单元是最稳定的空间构型,不存在倾覆问题;②运动灵活,通过改变运动形式以适应不同的环境,比如越障、穿越隧道、跨过沟渠等;③结构简单,便于模块化,可以组成多种多样的多面体机器人形式,在民用、军用及太空探测领域都有广阔的应用前景.

目前,对空间四面体翻滚机器人的研究比较少.NASA率先开展了四面体翻滚机器人样机的研究,迄今已经有 3代样机产生[3-5].现阶段只有第 1代样机实现了连续的翻滚运动,第 2、第 3代样机结构复杂,运动控制方法正在研究中.文献[6]描述了一个简易四面体翻滚机器人的制作方法,验证了四面体机器人翻滚的可能.国内北京交通大学的朱磊[7]等人吸取 NASA的设计灵感,提出了基于四杆机构的空间滚动步行移动机构,对该机构进行了运动学和动力学分析,具有运动学模型简单,方便控制,抗冲击能力强,对称性好等特点.但此机构和四面体翻滚机器人差别较大,前者是基于四杆机构提出的过约束六杆 SU机构,后者是一种杆长可变的桁架机构,运动方式和机构分析方法都有所不同.

由于空间四面体翻滚机器人独特的运动方式,其运动学和动力学分析方法也不同于目前传统机器人的分析方法.NASA虽然成功研制了第 1代样机,但是并未见到相关的理论分析研究.为此,本文结合四面体翻滚机器人的结构特点和运动形式,将一个翻滚周期分为 4个阶段:①翻滚前变形;②翻滚;③触地;④回复原状.对四面体机构进行了运动学分析.最后对机器人进行了运动学仿真和数据对比,研制的样机也成功完成了翻滚实验,验证了方法的正确性.

1 空间四面体机器人结构介绍

图 1为本文研究的空间四面体翻滚机器人的结构简图,它由 6根伸缩臂和 4个顶部节点平台组成,各伸缩臂的原始长度相同.4个节点平台将6根伸缩臂以虎克铰连接,节点和伸缩臂都可以自由运动.每个伸缩臂由一个电动机驱动,采用绳传动机构,通过电动机的正反转使之按照一定规律做大行程往复式伸缩运动,通过调整伸缩臂的个数和其伸缩比,产生不同的运动模式,实现空间四面体翻滚机器人的不同步态.

图 1 空间四面体翻滚机器人的结构图

2 翻滚临界条件

空间四面体翻滚机器人的运动模式有多种,本文选择其中一种运动模式进行分析,见图 2.DB和 DC两臂不伸长 lDC=lDB=l0;AD臂伸长后的杆长 lAD=l1,BC臂伸长后的杆长 lBC=l2;AB,AC两臂伸缩时以同一速度伸长,伸长后的杆长 lAB=lAC=l3.四面体将会发生以△ADM为镜面的对称变形(M为 BC的中点),变形到一定程度,重心偏离稳定区域[8-9],四面体将绕 BC轴发生翻滚,运动过程见图 2.这种情况下,△ADM各边长为

图 2 翻滚过程示意图

假设组成空间四面体翻滚机器人的各构件质量均匀分布,四面体与地面接触的△BCD就是其对应的稳定区域,可以确定,当满足下面条件时,四面体将发生翻滚:△ADM的中心 G(即四面体的重心)在地面上的投影 P与 M点重合或落在DM的延长线上,即 GP⊥DM.故有如下几何关系:

根据以上条件,可以得到此时各杆长应满足如下关系:

式(5)即为到达翻滚临界条件时各杆长应满足的关系.

4根伸缩臂等速同步伸长是上述运动形式的一种特殊情况,可得翻滚临界条件:

式中,ls为伸缩臂等速伸长后的杆长.

3 翻滚前变形的运动学分析

根据空间四面体机器人的结构特点和运动方式,建立如图 3所示的坐标系,基于顶点 D(翻滚前不动)的惯性坐标系{O0}和顶点坐标系{O1}.坐标系 O1x1y1z1的 z1轴与△ABC平面垂直,y1轴与△ABC的中线 AM重合,x1轴根据右手定则确定.由此可见,z1与 z0之间的夹角 α就是两平面 ABC和平面 BCD之间的二面角.

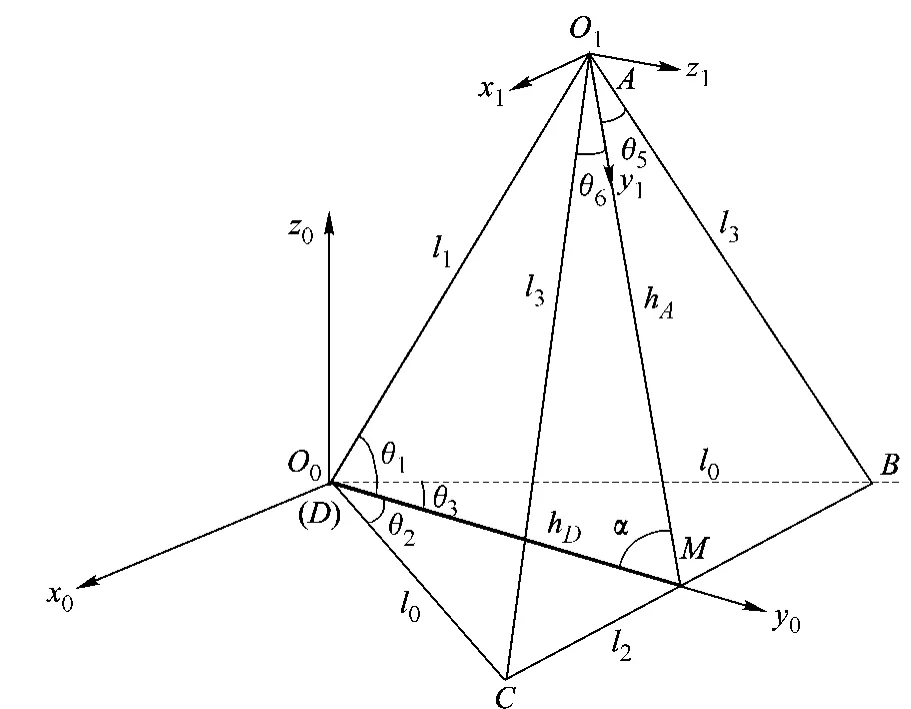
图 3 四面体翻滚机器人坐标系

从顶点坐标系 O1x1y1z1到惯性坐标系 O0x0y0z0的变换矩阵为

其中

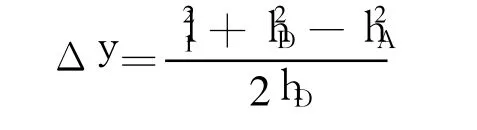
3.1 Jacobi矩阵

假设空间四面体翻滚机器人的构件 i质心位置、姿态分别用 Ωi,Φi表示,Ωi,Φi和各伸缩臂的驱动关节变量为非线性函数,可以表示为

将其对时间求一阶导数可得构件 i质心速度vi和角速度 ωi:

对时间求二阶导数得到构件i质心速度 ai和角速度εi:

JT,i和 JR,i分别称之为构件 i的平动部分 Jacobi矩阵和转动部分 Jacobi矩阵.

3.2 顶部节点的 Jacobi矩阵

以顶部节点 A为例,首先求得 A在惯性坐标系下的质心位置和姿态:[θ1,0,0,1]T,其中zA=Δz.于是有

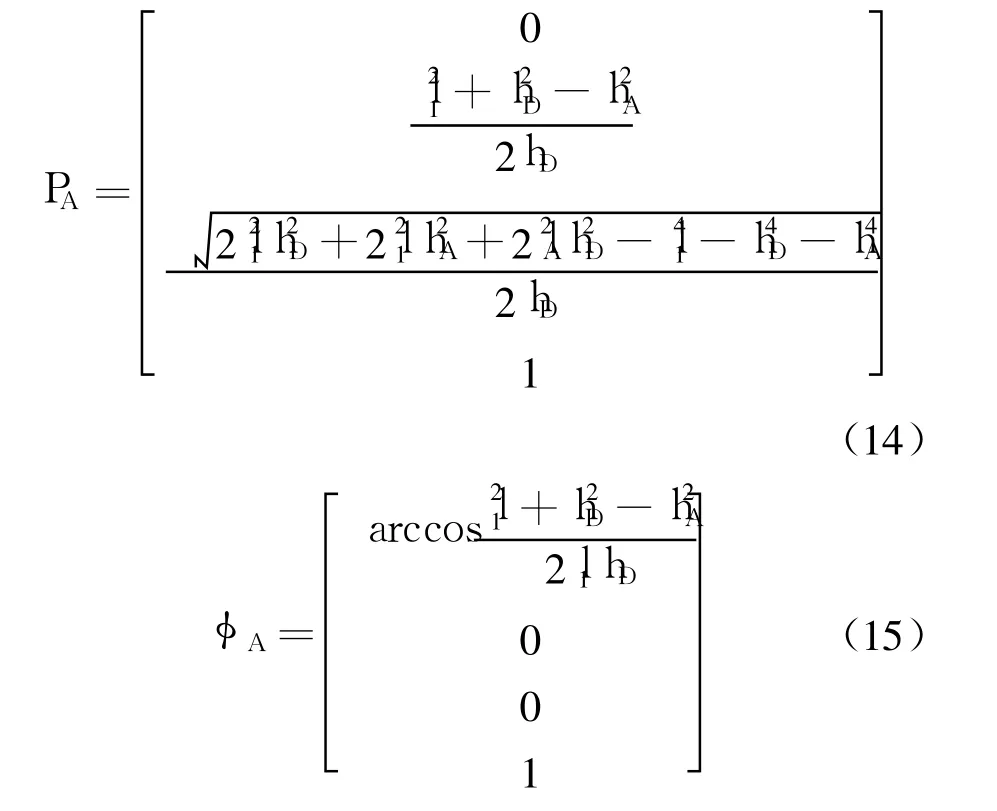
根据式(10)、式(11),对 PA,φA分别求关于l1,l2,l3的偏导数,得到固定构件 D1和活动构件U1的平动 Jacobi矩阵 JA,v和转动 Jacobi矩阵JA,w,即有速度

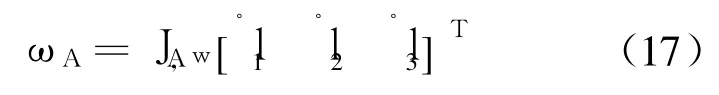
加速度

同样方法可以求得节点平台 B和 C的 Jacobi矩阵 JB,v,JB,w,JC,v,JC,w和相应的速度、加速度.

3.3 伸缩臂 AD,DB,DC,BC的 Jacobi矩阵

四面体翻滚机器人的伸缩臂由固定构件 Di和活动构件 Ui两个部分构成,伸缩臂 AD的固定构件 D1和活动构件 U1的质心坐标:

构件 Di,Ui的质心姿态相同,有

其中,ld,lu分别为固定构件的长度和活动构件的长度,6根伸缩臂相同.

根据式(10)、式(11),求得 D1和 U1的 Jacobi矩阵

同样方法可求得 DB,DC,BC伸缩臂的固定构件 Di和活动构件 Ui的 Jacobi矩阵.

3.4 伸缩臂 AB,AC的 Jacobi矩阵

伸缩臂 AB的固定构件 D5和活动构件 U5在顶点坐标系下的质心坐标:

D5和 U5的质心姿态相同,有

坐标变换到惯性坐标系下有

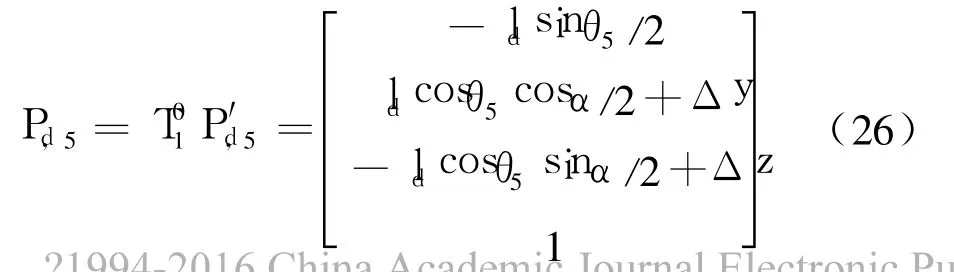
根据式(10)、式(11),求得 D5和 U5的 Jacobi矩阵 Jd5,v,Ju5,v,Jd5,w,Ju5,w.同样方法求得 AC的固定构件 D6和活动构件 U6的 Jacobi矩阵.

四面体翻滚机器人回复阶段的运动学分析方法可以参考翻滚前的方法,下文将不再赘述.

4 翻转阶段

图 2给出了空间四面体翻滚机器人从伸缩臂开始伸长到实现翻滚的示意图,可绕底面△BCD的任意一边为轴进行翻转.以绕 BC轴为例进行翻滚阶段的运动学分析,设杆 BC的向量为

节点 A和 D的期望翻滚路径可以表示如下:

其中 i=A,D.旋转矩阵

其中,φ是翻滚时刻△ABC与水平面的夹角;γ=1-cosφ是节点 i的初始位置;是节点 i的需要位置.通过选择不同的翻滚轴,可以规划出四面体机器人行进的不同路径.

图 4 空间四面体翻滚机器人的运动轨迹

图 4是绕不同轴翻滚时空间四面体翻滚机器人的运动轨迹,可以看出,四面体在运动过程中可以随时改变行进方向,具有非常大的灵活性,所以说它对非结构化的环境具有很强的适应性.

5 触地阶段

将四面体翻滚机器人简化为刚体,因此可以将整个机构的质量集中在一点,如图 5.设触地时地面的冲击力为 R,列写牛顿方程和欧拉方程:

其中,r是质心(mC)到 nA的位置矢量;mC是将四面体翻滚机器人简化为刚体后的质量;nC是质心的位置矢量;IC,wC,αC分别是与之对应的刚体转动惯量,转动角速度,加速度.

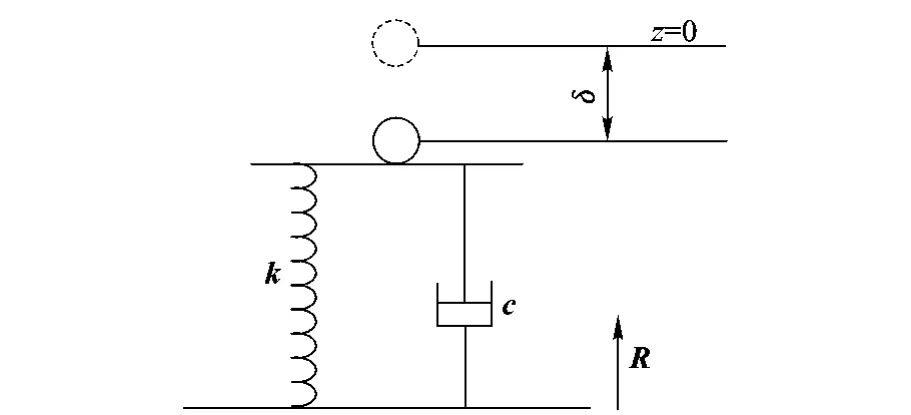
图 5 空间四面体翻滚机器人触地时的动态模型

将四面体顶部节点触地的过程看作是一个线性弹簧-阻尼系统[10-11],如图 5,有

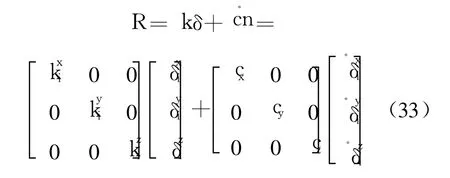
其中,k和 c是弹簧和阻尼矩阵;δi是落地节点与地面接触时的微小位移;顶部节点的接触力 R与位移 δ和对应的速度·δ成正比.

ii

6 仿真与实验

为了验证运动学分析方法的有效性,建立了四面体翻滚机器人的仿真模型,按照上面所述的运动模式,使模型在水平面完成翻滚的动作.仿真模型的参数如下:伸缩臂原始长度 l0=1 000mm,固定构件长度 ld=900mm,活动构件长度 lu=960mm.伸缩臂的初速度为零,四根伸缩臂等速伸长,运动规律如下:0～2 s,匀加速伸长,加速度a=150mm/s2;2～3s,匀速伸长,a=0;3～4s,匀减速伸长,a=-300mm/s2;4 s～te,自由落体.

仿真结果表明,空间四面体翻滚机器人能够按照上述运动模式实现翻滚动作,如图 6.在 t=4.0s时刻,到达翻滚临界条件,伸缩臂的长度约为 1715mm,与几何翻滚临界条件基本一致.稍有差别的原因除了仿真模型和运动学模型的建模误差外,主要是由于文中给出的翻滚临界条件只是从几何学的角度考虑,暂时还没有考虑动力学的影响.现阶段都是在伸缩臂运动速度比较小的情况下翻滚,但当在运动速度增大的情况下,动力学的影响将加大,下阶段工作将对此展开深入研究.

图 6 空间四面体翻滚机器人的运动仿真结果

图 7 空间四面体翻滚机器人样机实验

图 7是开发的空间四面体翻滚机器人原理样机,通过实验可以看出,机器人能够按照预设的运动路径实现翻滚动作,并且回复原状,完成一个翻滚周期的运动.下一步动作可以根据运动需要选择翻滚轴,并且方向、步长、高度等都可以灵活掌握.与同等大小的其他类型机器人相比,具有结构简单、稳定性高、运动灵活等诸多优点,在危险场合作业、军事侦察、太空探测等领域都有广阔的应用前景.

7 数据分析

图 8a为用文中方法得到的四面体翻滚机器人顶部节点 A在高度方向(z方向)的位置曲线,图 8b为与之对应的仿真模型的位置曲线.

图 9a为用文中方法得到的四面体翻滚机器人顶部节点 A在 z方向的速度曲线,图 9b为与之对应的仿真模型的速度曲线.

图8 顶部节点 A在z方向的位置曲线

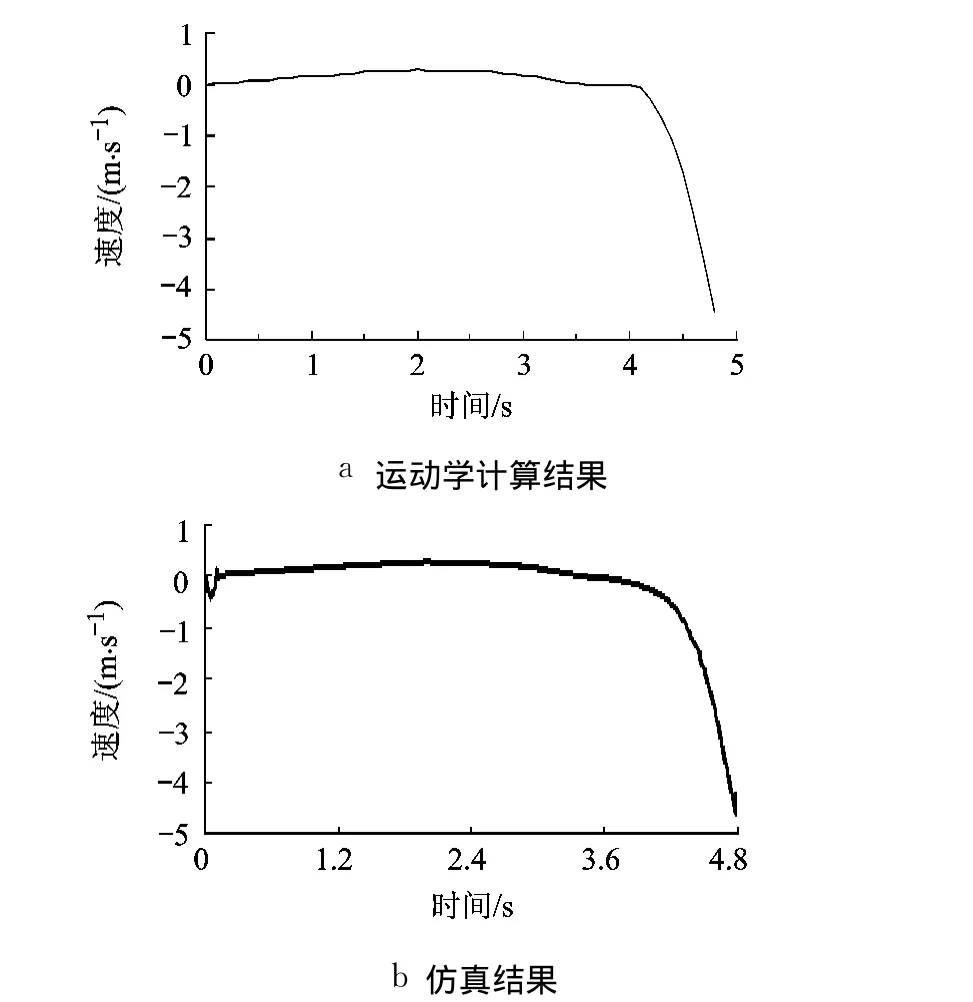
图9 顶部节点 A在z方向的速度曲线

可以看出,仿真曲线与理论曲线基本一致,仿真模型较好地反映了实际模型,证明本文提出的运动学分析方法的正确性.在某些地方,曲线有些微小差异,主要是由于仿真模型和运动学模型的建模误差(仿真模型中在 t=4.8 s时顶点触地).

图 10为顶部节点撞击地面时的受力图.可以看出,翻滚时刻节点速度大将导致撞击地面时的冲击力增大,验证了触地阶段的分析模型.据此,可以得到合理控制翻滚时刻的节点速度,顶部节点选择弹性材料包裹,可以达到减小冲击力的目的.本文设计的四面体翻滚机器人的顶部节点采用橡胶包裹,起到了很好的减震作用.

图 10 顶部节点撞击地面时的受力对比图

8 结 论

1)介绍了空间四面体翻滚机器人的结构,结合运动特点,分阶段进行了运动学分析;

2)利用 Adams虚拟样机平台建立了空间四面体翻滚机器人的运动学模型,通过仿真验证了本文所提运动学分析方法的正确性,该运动学模型能准确反映空间四面体翻滚机器人的运动情况;

3)进行了空间四面体翻滚机器人的样机实验,也验证了上述理论分析的正确性:

4)本文研究对此类型机构的动力学分析、优化设计和控制具有重要的参考价值.

References)

[1]Hamlin and G J,Sanderson A C.A novel concentric multi link spherical joint with parallel robotics applications[C]//Proceedings of the IEEE International Conference on Robotics＆Automation.San Francisco:IEEE,1994:1267-1272

[2]Hamlinand G J,Sanderson A C.Tetrobot a modular approach to reconfigurable parallel robotics[M].MA:K luwer Academic,1997

[3]Clark P E,Curtis S A,Rilee M L.Extrememobility:Next generation tetrahedral rovers[C]//Space Technology and Applications International Forum-STAIF.Washington DC:American Institute of Physics,2007:711-718

[4]Clark P E,Rilee M L,Curtis SA.BEES for ANTS:Spacem ission applications for the autonomous nanotechnology swarm[C]//A IAA 1st Intelligent Systems Technical Conference.Chicago:lllinois American Institute of Aeronautics and Astronautics,2004:1-12

[5]Curtis S,Brandt M,Bowers G,et al.Tetrahedral robotics for space exploration[J].IEEE Aerospace and Electronics Systems Magazine,2007,22(6):22-30

[6]A brahantes M,Silver A,Wendt L,et al.Construction and control of a 4-tetrahedron walker robot[C]//40th Southeastern Symposium on System Theory.New Orleans:University of New Orleans,2008:343-346

[7]朱磊.基于四杆机构的空间滚动步行移动机构研究[D].北京交通大学机械与电子控制工程学院,2008 Zhu Lei.The research of a spatial rolling-walk mobile mechanism based on four-bar mechanism[D].Beijing:School of Mechanical,Electronic and Control Engineering,Beijing Jiaotong University,2008(in Chinese)

[8]Zhang Lige,Bi Shusheng.Dynamic legmotion generation of humanoid robot based on human motion capture[C]//Proceedings of the IEEE International Conference on Intelligent Robotics and Applications.Berlin:Springer-Verlag,2008:83-92

[9]Peng Zhaoqin,Huang Qiang,Zhang Lige,et al.Humanoid online pattern generation based on parameters of off-line typical walk patterns[C]//Proceedings of the IEEE International Conference on Robotics and Automation.Barcelona:IEEE,2005:3769-3774

[10]Lee Woo Ho,Sanderson Arthur C.Dynamic rolling locomotion and control of modular robots[J].IEEE Transactions on Robotics and Automation,2002,18(1):32-41

[11]Lee Woo Ho,Sanderson Arthur C.Dynamic rolling of modular robots[C]//Proceedings of the 2000 IEEE International Conference on Robotics＆Automation.San Francisco:IEEE,2000:2840-2846

(编 辑:文丽芳)

Motion analysis and simulation of tetrahedral rolling robot

Zhang Lige BiShusheng

(School of Mechanical Engineering and Automation,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)

Peng Zhaoqin

(School of Automation Science and Electrical Engineering,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)

The research status of tetrahedral robot was analyzed.The mechanism of tetrahedral rolling robot was introduced.The robot comprises of six extension struts and four node flats.When the center of gravity(COG)of tetrahedron exceeds the stability region,the robot will roll.Kinematic model in different motion phase was analyzed according to the structure and motion characteristic of the tetrahedral robot,and the rolling critical condition was formulated.The simulation model was built by virtual flats oft ware Adams,and the effectiveness of the method was testified through simulation and experiment.The results provide important reference for the dynamic analysis,optimization design and control of the tetrahedral rolling robot.

tetrahedral rolling robot;kinematic analysis;rolling critical condition;motion simulation

TP 242

A

1001-5965(2011)04-0415-06

2010-01-21

张利格(1978-),女,北京人,博士后,zhanglige@buaa.edu.cn.