变电站接地系统的优化设计

于建立，李艳飞，胡国伟

(东北电力大学，吉林吉林132012)

0 引言

随着电力系统电压水平的不断提高和系统容量的不断增大，接地故障电流和接地网的面积就会不断增大。所以，为了确保人身和设备的安全，维护系统的可靠运行，不但要改变降低接地电阻的传统观念，而且要考虑电位梯度所带来的危险。对此，本文采用数值计算法得到均匀和不均匀土壤中最优压缩比的计算公式，以获取接地网优化设计方法。

1 接地网的不等电位数学模型

计算接地网工频接地参数需同时考虑导体向大地的漏电流［5］、导体轴向电流在导体内电阻、自感上产生的压降和在其它导体上产生的互感压降。图1为1个简单的田字形接地网示意图，短路电流从1个边角节点入地，并假设每段导体的漏电流集中在导体中点入地。

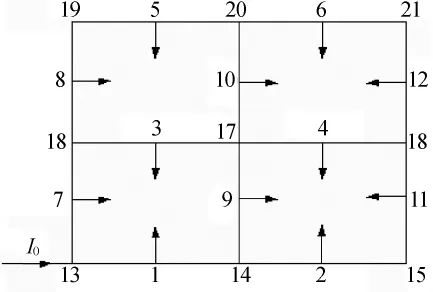
图1 接地网示意图

应用电路理论中的节点分析方法建立节点关联矩阵A，可以求得接地网络阻抗矩阵z，关系表达式为

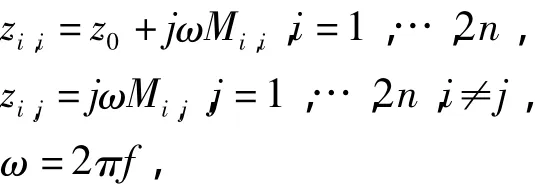
式中z0、Mi，i和Mi，j分别为网络变成2n条支路后每条支路导体的内阻抗、外自感和不同导体间的互感［6］;f为入地电流的频率。对图1所示电路列出节点电压方程，关系表达式为

由于每段导体漏电流会在所有导体表面上产生电位，因此第j段导体上的总电位为

式中Rij为互电阻。采用点匹配矩量法将式(3)写成矩阵的形式，则有

漏电流可表示为

将式(4)代入式(2)，整理后可得

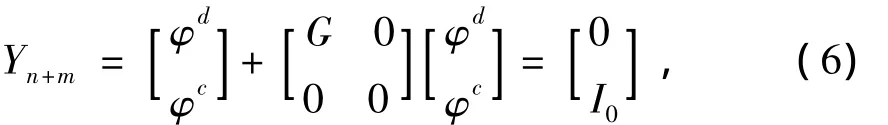
若将(n+m)阶方阵Yn+m分成4块，则可得

式中Ynn和Ymm分别为n阶和m阶方阵;Ynm为n行m列矩阵。由式(7)可得

以上是不等电位的数学模型，本模型全面地考虑了导体电阻、自感和导体间的互感，故计算结果更符合实际情况。

2 最优压缩比的原则

普通接地网一般采用等间距布置，即接地网导体之间的间距基本相等;考虑到接地网对中间部分导体的屏蔽性，网中导体的布置可采用中间稀疏四周密集的不等间距方法，所有导体的散流所用得到充分利用［7］。本文导体间距采用从边缘到中心按指数规律逐渐增加的布置原则，并通过计算证明该方法比接地网等间距布置合理，如图2所示。

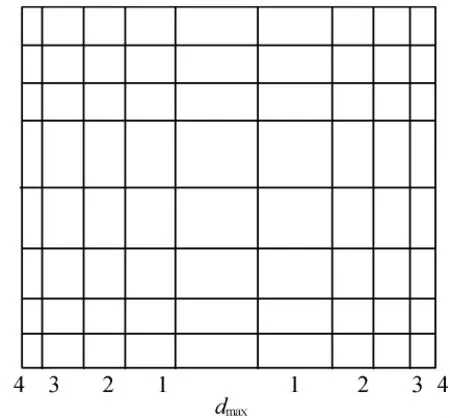
图2 按指数分布接地图示意图

该布置方案不仅可以降低地表电位梯度，同时也是1种安全、经济的设计方法。导体之间按指数分布，距离中心网孔为n级网孔，网孔间距dn= dmaxcn，显然压缩比c＜1。dmax为中心网孔边长(即最大网孔边长)，在长度为l的水平导体上不等间距排列n根导体时，可得到中心网孔间距为

根据发电站、变电站接地装置的接触电压和跨步电压允许值计算公式［8-9］，得到的跨步电压允许值比接触电压允许值高，而绝大多数情况下实际地网的跨步电压最大值均比接触电压的最大值低很多。在设计接地网时只需考虑接触电压的最大值，接触电压达到安全标准，跨步电压自然符合安全要求。因此，在设计接地网时，应以接触电压的最大值和最小值之差最小时建立目标函数，求得最优压缩比。

3 各种因素对最优压缩比c影响

3.1 均匀土壤影响最优压缩比的因素

在均匀土壤条件下，接地网面积大小、土壤电阻率、接地网单方向的导体根数等因素皆可对c产生影响。本文以数值计算方法对以上各因素的影响进行了分析，计算参数选择土壤电阻率 ρ为60 Ω·m;网孔数为20×20;导体埋深为0.8 m;导体等效半径为0.01 m;导体电阻率为1.7×10-7Ω·m;电流为1 A，从地网中心注入。图3为接地网边长与最优压缩比关系。由图3可见，最优压缩比随着接地网的边长增大而增大，即接地网的某个方向的边长越长则这个方向水平导体分布越均匀。图4为土壤电阻率与最优压缩比关系。接地网边长取300 m，只改变土壤电阻率，其它参数同上。图4表明ρ增大时最优压缩比就会减小，接地网的网孔间距不均匀。

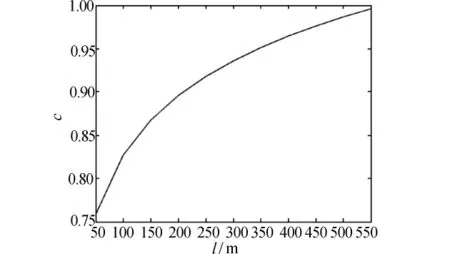
图3 接地网边长与最优压缩比关系

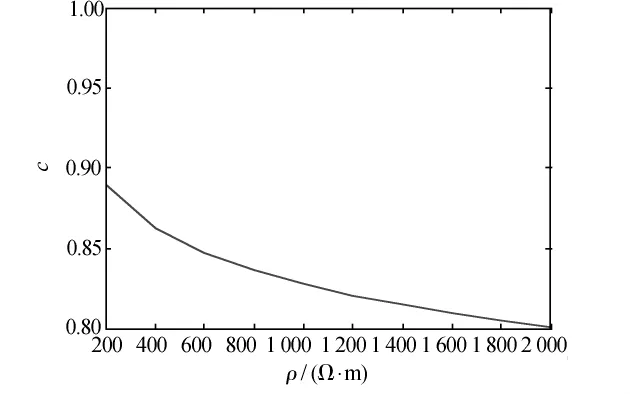
图4 土壤电阻率与最优压缩比关系

图5为单方向导体根数与最优压缩比关系。ρ为200Ω·m，接地网面积取200 m×200 m，其它参数同上。图4表明接地网面积一定时最优压缩比随导体根数的增加而增大，导体根数增多，网孔间距会更趋于均匀。

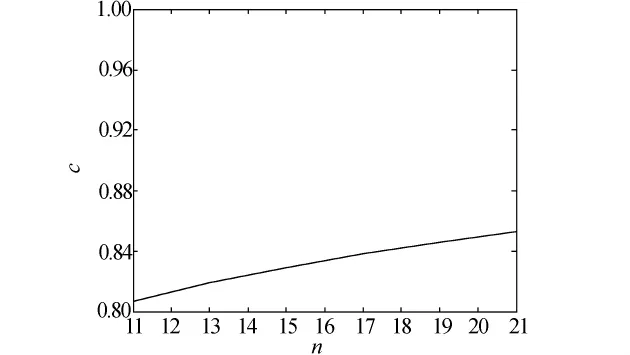
图5 单方向导体根数与最优压缩比关系

3.2 非均匀土壤影响最优压缩比的因素

大量工程经验表明，不均匀土壤中影响c的因素为上层土壤厚度h、反射系数k、接地网面积等。以2层土壤为例，计算参数接地网面积为100 m× 100 m，反射系数分别是±0.95、±0.60、±0.30。图6表示最优压缩比与上层土壤厚度关系。由图6可见，反射系数(k＜0)一定时，最优压缩比先随上层土壤厚度增大而增大;当h达到一定数值后，最优压缩比c达到最大值，然后随h的增大而逐渐减小，表明下层土壤电阻率比上层土壤电阻率小;上层土壤厚度h达到一定范围时，最优布置的接地网的水平导体分布较均匀。随着h的增大、c减少，接地网水平导体的分布出现不均匀现象。k＞0时，最优压缩比先随上层土壤厚度增大而减少，当h达到一定数值后，最优压缩比也达到最小值，然后随h的增大，c逐渐增大。因此，下层土壤电阻率比上层土壤电阻率大、上层土壤厚度h增大到一定范围时，最优布置的接地网的水平导体分布不均匀，随着h的增大而减少。当反射系数k趋近于零时，最优压缩比受上层土壤厚度h影响较小。

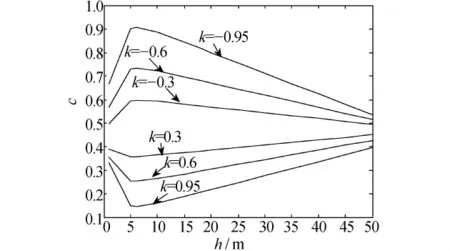
图6 最优压缩比与上层土壤厚度关系

图7为最优压缩比与反射系数的关系。计算参数为以下2种情况:h为10 m，接地网面积为200 m×200 m，单方向导体根数为15;h为20 m，接地网面积为300 m×300 m，单方向导体根数为16。当上层土壤厚度一定时，最优压缩比c随k的增大而减少，任何h值下最优压缩比c总是在k＜0比k＞0时大。

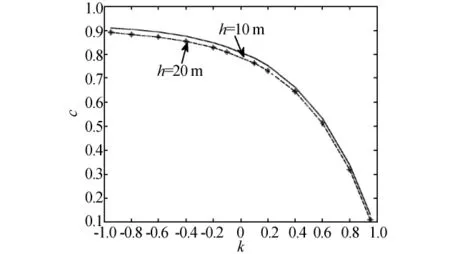
图7 最优压缩比与反射系数关系

4 最优压缩比c拟合公式

以最小二乘法拟合曲线。在均匀土壤时，可以得到最优压缩比c与l、n、ρ之间的关系式，采用的拟合表达式为

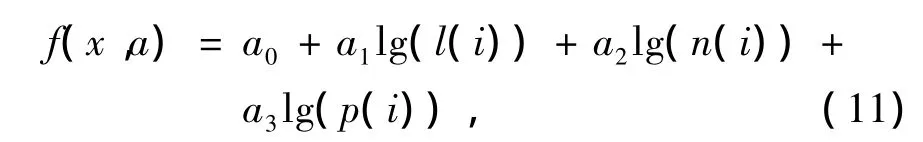
式中a0、a1、a2、a3优化计算的数据分别为0.013 4、0.098 8、0.071 3、-0.038 5。

在非均匀土壤时，采用的公式为

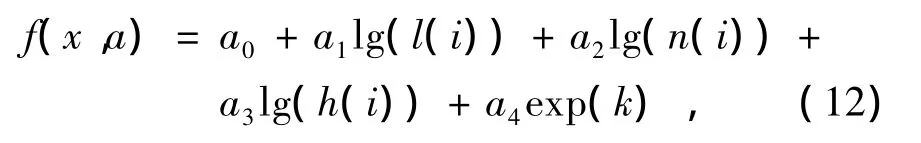
式中 a0、a1、a2、a3、a4优化计算的数据分别为0.012 8、0.066 0、0.101 5、-0.019 4、-0.119 3。

5 结论

a.采用不等电位的计算模型，能真实地反映接地网电位分布情况。

b.确定最优压缩比以接触电压的最大值与最小值之差最小作为目标函数，使计算更合理，结果较理想。

c.在均匀土壤中，最优压缩比随接地网边长的增加而增大，随单方向导体根数的增加而增大，随土壤电阻率的增大而减少。在非均匀土壤(本文以2层土壤为例)中，反射系数为负值时，最优压缩比先随上层土壤厚度h的增加而增大，达到最大值后逐渐减小。反射系数为正值时，最优压缩比先随h的增大而减小，达到最小值后逐渐增加。反射系数越接近于零，最优压缩比受h的影响越小。最优压缩比随反射系数的增大而减小，下层土壤电阻率低于上层时最优布置的水平导体，比下层土壤电阻率高于上层时分布更均匀。最优压缩比与接地网边长的关系与均匀土壤变化相同。

［1］ Sverak J G.Optimized Grounding Grids Design Using Variable Spacing Techniques［J］.IEEE T-PAS，1976，95(1):362 -374.

［2］ Dawalibi F，Mukhedkar D.Optimum design of substation grounding in a two layer earth structure，part 1:analytical study［J］. IEEE T-PAS，1975，94(2):252-261.

［3］ Dawalibi F，Mukhedkar D.Optimum design of substation grounding in a two layer earth structure，partⅡ:comparison between theoretical and experimental results［J］.IEEE T-PAS，1975，94 (2):262-266.

［4］ Dawalibi F，Mukhedkar D.Optimum design of substation grounding in a two layer earth structure，parⅢ:study of grounding grids performance and new electrode configuration［J］.IEEE TPAS，1975，94(2):267-272.

［5］ 鲁志伟，文习山，史艳玲.大型变电站接地网工频接地参数的数值计算［J］.中国电机工程学报，2003，3(12):89-93.

［6］ 卡兰塔罗夫，采伊特林.电感计算手册［M］.陈汤铭译.北京:机械工业出版社，1984.

［7］ 高延庆，何金良，曾嵘.发电站、变电站接地网安全性能分析［J］.中国电力，2001，34(5):33-36.

［8］ Hyung-Soo Lee，Jung-Hoon Kim.Efficient ground grid designs in layered soils［J］.IEEE Transaction on Power Deliery，1998，13 (3):745-751.

［9］ 中华人民共和国电力工业部.DL/T621-1997交流电气装置的接地［S］.北京:水利电力出版社，1998:83-93.