明渠水声信号测速方法研究

王 婧，刘纪元 ，焦学峰，张 皓

（1.沈阳航空航天大学 电子信息工程学院，辽宁 沈阳 110136；2.中国科学院声学研究所综合声纳实验室 北京 100080；3.北京航瑞博泰科技有限公司 北京 100102）

在注重节省能源，提高经济效益和产品质量的今天，流量计量与测试的重要更加突出并为越来越多的人所认识。特别是随着现代工业生产的飞速发展，人们对流量测量的要求越来越高，对流量测量技术和仪表的研究和开发不断深入，流量测量方法仪表的种类也越来越多。在一些大型引水场合，如：城市供水引水渠，火电厂引水和排水渠，污水治理流入和排放渠，工矿企业水排放以及水利工程和农业灌溉用渠道，明渠流量计发挥极其重要的作用。而超声波明渠流量计中影响流量的一个重要因素就是水速的测量及其精度，因此合理获取精确的水流速显得至关重要。

图1 多普勒原理图Fig.1 Doppler schematic

1 水声测速的基本原理

水声测速的原理图如图1所示。

在换能器收发共置的情况下，声波经发射后，测量声波被水中移动的悬浮物质反射，此时回波信号与发射信号就会产生频率差，即多普勒频移，利用频移就可以计算流速。

在一个测量周期内，首先换能器以发射频率fc发射一束超声波，这束波被一个悬浮质以与发射频率不同的频率接收到（或反射），这一过程就产生了多普勒频移，然后波束又一次反射回换能器，再一次产生一个多普勒频移。两个多普勒频移存在于这个交换过程中，前一个是信号通过换能器传到悬浮质，第二个是信号从悬浮质反射回换能器。

应用多普勒原理，同时考虑发射角α可以推导以下结论：

式中，c为声波在水中的传播速度，常温下大约1 500 m/s；v水为水流流速；fc为声源发射信号频率；α为发射信号与水平面的夹角。

在测量的过程中，由于v水＜＜c，公式简化为：

因此，要计算多普勒频移，只要将所接收到的回波做FFT后与水静止时的FFT做差，就可以得到频移f频移，从而得到水的流速V水。

2 三种方法概述

2.1 叠加法

顾名思义，叠加法就是取多次回波频谱将其相加，这样做的好处是，经过多次叠加，一些随机噪声的幅值随着叠加次数的增多增长很缓慢，但信号的频谱却增长明显，因此信号越来越突出，而噪声信号则越来越不明显了[1]，证明如下。

设每次测得频率为fi，每次测量值是互相独立的随机量，设其方δ2差均为，进行N次独立测量后的样本均值为

方差为

可见叠加的次数越多，效果越好，但是为能够反映当前水速值，测量时间不宜过长（次数不宜太多）。

2.2 谱减法

与语音信号的“谱减法”[2]不同的是，“回波谱减法”不是减去“寂静段”的噪声功率谱，而是带信号去噪。步骤如下：

1）首先发射换能器不发射信号，观察回波频谱，确定干扰的大概范围R。

2）调整水流速，使其对应的频谱在R之外，保存R内的数值。本步骤执行多次。

3）根据上一步骤整理数值，看干扰R内的数值与主频值的比例关系及主频与真实多普勒频率值的关系。

4）在接收的回波信号中依据比例减去干扰。

2.3 全相位频谱校正法

通过式（4）可以看出，水速的获得是通过回波的频率获得的，要想提高测速的精确度，就要知道回波的精确频率。如果真正的频率在两根谱线之间，则误差最大，为半个频率分辨率[3]。因此频谱校正对于提高测量精度是很必要的。传统FFT结果可以通过一些算法实现频谱校正，如能量重心法、比值法等。但以上的频率估计都是在传统的FFT架构下进行的，因而传统FFT固有的频谱泄露效应无疑会在很大程度上影响这些校正法的精度。全相位FFT算法（apFFT）具有初始相位不变和有效防止频谱泄露的特性[4]。

在图 2 中，ω*代表信号的数字角频率，k*=[ω*/Δω]（“[]”代表四舍五入），Δω 是角频率分辨率ω^*，A^，及θ^0为校正后的角频率、幅值及相位。

图2 FFT/apFFT综合相位差法的频谱校正流程Fig.2 The spectra calibrating process of FFT/apFFT method

由图2可以看出，FFT/apFFT综合相位差法需要对序列进行2次谱分析，一次传统FFT分析，一次全相位FFT谱分析。双窗全相位FFT过程，即对数据进行全相位预处理，然后进行传统的FFT运算。过程如下：

1）构成一个N点的汉宁窗；

2）汉宁窗对自己求卷积，得到2N－1点的卷积窗；

3）求2N－1点的卷积窗的和；

4）将卷积窗的每一项除以卷积窗的和，得到2N－1点的归一化卷积窗；

5）将数据的1到2N－1项和归一化卷积窗相乘，得到加窗的2N－1项；

6）将第 1项和 N+1项，第 2项和 N+2项 ...第 N－1项和第2N－1项相加，得到经过全相预处理的N点序列；

7）对6）中的经过全相位处理的N点序列做FFT运算；

以下简单介绍FFT/apFFT。

已知单频复指数信号为

信号的数字频率ω*表示为β倍频率间隔2π/N的形式（β可以是小数）。

其归一化的FFTapFFT谱：

其归一化的apFFT谱：

FFT/apFFT校正法需要2N－1个样点。对后N点作FFT，对全部的2N－1点作apFFT。对频率值β取整或从振幅谱可确定谱峰位置位于 k0=[β]处，[]表示取整，ang（.）表示取相操作。

由式（9）可知，在k0的apFFT的初始相位值φ0，则相位校正值：

由式（8）和（9）可知，在k0的FFT的相位值减去apFFT的相位值可得校正后的频率值β：

由式（7）和（8）可知，在的FFT的振幅值平方除以apFFT振幅即得校正后的振幅A:

3 结果分析

3.1 未加任何处理的回波波形

图3为未加任何处理的静水中的回波信号频谱图。

图3 静水中的回波信号频谱图Fig.3 Echo signal spectrum of still water

经过采样后的回波信号的余频所在的谱线数在409.6≈410根处。

图3以及下面的图4、图5、图6的横轴代表的是谱线根数，单位为频率分辨率，即fs/N Hz，N为FFT点数。纵轴是对采集到的数字信号做FFT后取绝对值。单位为10/216V。

在上图的回波波形中可以看出，回波有噪声干扰。

3.2 叠加后的频谱图

叠加后的静水及水流动的回波频谱图如图4所示。

图4 叠加后的静水及水流动的回波频谱图Fig.4 Superposed echo spectrum of still water and flowing water

由上图可以看出，叠加后的频谱图轮廓清晰，峰值明显，噪声与信号的频谱比较，微乎其微。但是此时的主频处410根谱线的峰值仍然大于真实谱线处的峰值 （410根右侧的那个峰值）。

3.3 叠加+谱减法后的频谱图

图5为静水中叠加及谱减法后的回波频谱图。

图5 静水中叠加及谱减法后的回波频谱图Fig.5 Echo spectrum after superposition and spectral subtraction of still water

从图6中可以看到，频谱图稍乱一些，这是由于系数选取的缘故，因为所选取的系数是多次测量取的平均值。但是回波的波形不是固定不变的，所以经过处理后的频谱图为当前的状态，但是这不会影响判断结果。

图6 水流动叠加及谱减法后的回波频谱图Fig.6 Echo spectrum after superposition and spectral subtraction of flowing water

现在已经可以看出主频处410根谱线的峰值不再大于真实值谱线处的峰值了。当测量真实结果在R谱线范围内，谱减法后的频谱也不会影响真实值的判断。因此此种办法有一定效果[6-7]。

3.4 FFT/apFFT校正前后对比

发射的信号频率为：1 MHz；信号幅值：0.8 V；初相：180；采样频率：25.51 kHz；FFT/apFFT分析校正后的频谱如图7所示，表1列出了校正前后数据（静水）。

在图7中，横坐标k表示的是谱线根数，单位为频率分辨率，即fs/N Hz，N为FFT点数。纵坐标y1表示的是加窗后的FFT振幅谱，单位为V；y2表示的是振幅谱，单位为V；y3代表的是apFFT的相位谱，单位为（°）；y4表示的是归一化的相位偏离校正值，单位为Δf Hz，Δf代表频率分辨率；y5表示的是振幅校正值，单位为V[8-9]。

注意这里是欠采样，所以回波频率指的都是余频。为了考核此种方法的可行性及稳定性，在常温下做了多组实验来验证。调节水速从而使回波产生不同的频率，通过综合应用方法对回波频率进行校正（噪声的幅值大约是信号幅值的0.1倍）。整理后的结果如表2所示。其中公式（4）中 α 的取 30°。

图7 FFT/apFFT频谱校正Fig.7 FFT/apFFTspectrum correction

表1 FFT/apFFT频谱校正结果前后数值Tab.1 Results before and after FFT/apFFT correction

由于测速关心的主要问题是回波的频率，故表2里只对频率的校正前后做了对比。此处，相对误差=（测量值-理论理）/理论值。

由式（4）可知，多普勒频移的相对误差就是水速的相对误差。因此在计算水速的相对误差时，可以通过计算多普勒频移的相对误差来获得水速的相对误差，减少计算量。

以第1组数据为例：

f频移=5 159.735-5 102=57.735 Hz

由表中的数据可以看出，在有噪声的情况下，校正后的相对误差比校正前的相对误差减低了很多，相对误差基本降低了一个数量级。此方法在水速测量上对提高测度精度是起到了一定的作用。

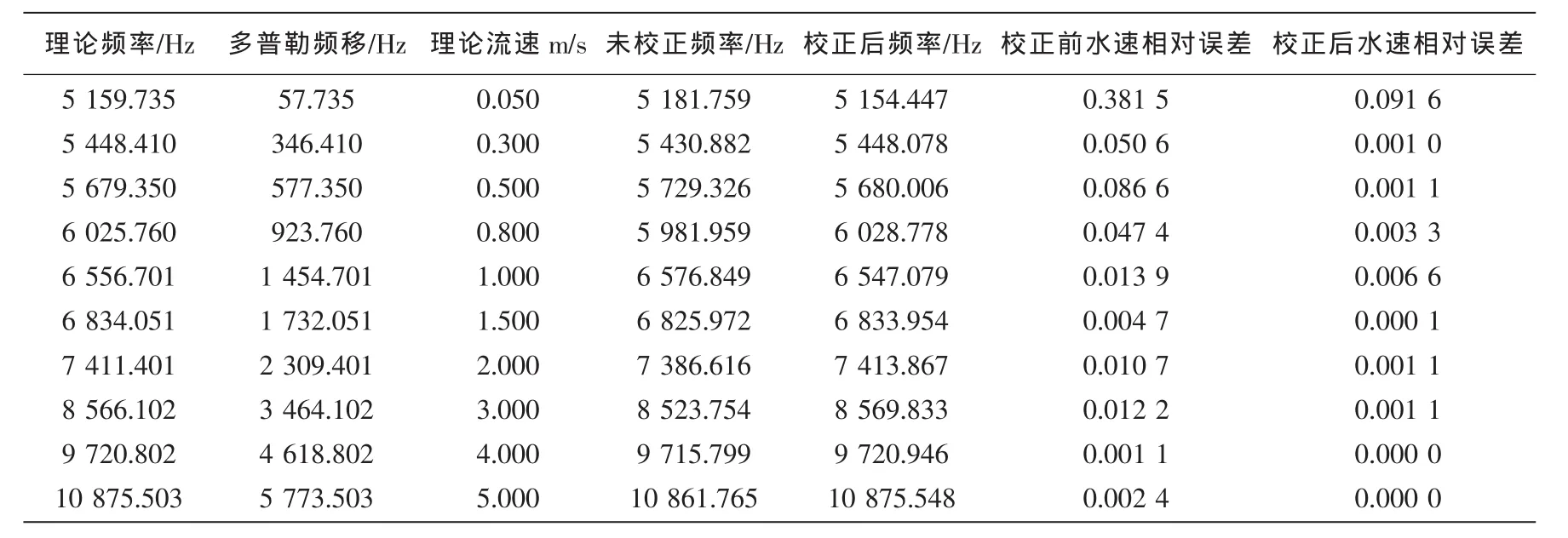
表2 FFT/apFFT频谱校正方法测试数据Tab.2 Test data of FFT/apFFT correction

4 结 论

本文在设计中将“叠加法”、“谱减法”及“全相位频谱校正法”结合应用于水速测量中。这些处理方法的结合，一方面可以降低噪声干扰，突出信号，另一方面降低了主频对其他频率的干扰。特别是全相位频谱校正方法的引用，可以避免

离散频谱引起的误差，能够在有噪声的情况下，将误差降低一个数量级。

[1] 高晋占.微弱信号检测[M].北京:清华大学出版社，2002.

[2] 杨行峻，迟惠生.语音信号数字处理[M].北京:电子工业出版社，1995.

[3] 丁康，谢明，杨志坚.频谱分析校正理论与技术[M].北京:科学出版社，2008.

[4]王兆华，黄翔东.数字信号全相位频谱分析与滤波技术[M].北京:电子工业出版社，2009.

[5] 黄翔东，王兆华.基于全相位频谱分析的相位差频谱校正法[J].电子与信息学报，2008，30（2）：293-297.HANG Xiang-dong，WANG Zhao-hua.Phasedifference correcting spectrum method based on all-phase spectrum analysis[J].Journal of Electronics&Information Technology，2008，30（2）:293-297.

[6] 李启虎.声纳信号处理引论[M].北京:海洋出版社，1985.

[7] 俞小鼎.多普勒天气雷达原理与业务应用[M].北京:气象出版社，2006.

[8] 张贤达.现代信号处理[M].北京：清华大学出版社，2002.

[9] 刘波，文忠，等.MATLAB信号处理[M].北京：电子工业出版社，2006.