基于模拟退火的自适应图像滤波算法

邓平，方志祥，熊盛武

（1.武汉理工大学计算机学院，湖北武汉430070；2.武汉大学测绘遥感信息工程国家重点实验室，湖北武汉430070）

在图像处理中，图像噪声可以理解为妨碍人的视觉感知，或妨碍系统传感器对所接受图像源信息进行理解或分析的各种因素，也可以理解成真实信号与理想信号之间存在的偏差。一般来说，噪声是不可预测的随机信号，通常采用概率统计的方法对其进行分析。噪声对图像处理十分重要，它影响图像处理的各个环节，特别在图像的输入、采集中的噪声抑制是十分关键的问题。图像去除噪声有很多种滤波方法，传统的可分为以局部平均法为代表的线性滤波和以中值算法为代表的非线性滤波，中值滤波适用于椒盐型噪声，均值滤波适用于高斯型噪声。邻域平均法是一种在局部空间域求值的算法，在降低噪声的同时，使图像产生了模糊，特别是在处理图像边缘和细节的时候。中值滤波法在一定程度可以克服线性滤波所带来的图像细节模糊，但是对一些点、线、突变等细节图像会带来图像信息的丢失。本文提出的图像去噪算法是基于模拟退火算法，可以在指定领域内，以一定的概率接受偏离中值的点，这样既有非线性滤波的优点，同时又可以克服中值滤波对图像信息的丢失问题，实验表明该算法能够较好的提高图像的信噪比。

1 模拟退火算法

模拟退火算法是一种快速收敛的概率演算法[1]，用来在一个搜索空间内寻找命题的最优解。“模拟退火”的原理也和金属退火的原理近似：将搜寻空间内每一点想象成空气内的分子；分子的能量，就是它本身的动能；而搜寻空间内的每一点，也像空气分子一样带有“能量”，以表示该点对命题的合适程度。算法先以搜寻空间内一个任意点作起始：每一部先选择一个“邻居”，然后再计算从现有位置到达“邻居”的概率。

面对寻找最优值的优化问题。将物理学中模拟退火的思想应用与优化问题得到模拟退火寻优方法。

优化函数为f:x→R+，其中x∈S，它表示优化问题的一个可行解，R+={y|y∈R，y＞0}，S表示函数的定义域。N（x）⊆S表示的一个领域集合。

首先给定一个初始温度T0和该优化问题的一个初始解x（0），并由x（0）生成下一个解x′∈N（x（0）），是否接受x′作为一个新解x（1）依赖于下面概率：

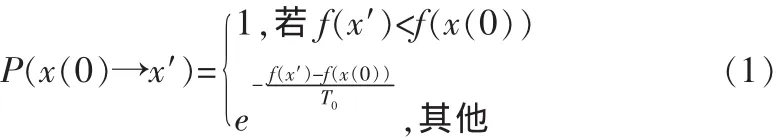
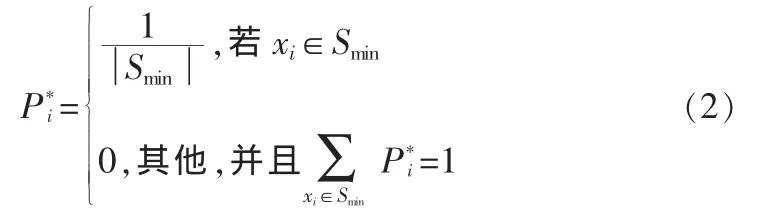
当温度T降为0时，xi的分布为：这说明如果温度下降十分缓慢，而在每个温度都有足够多次的状态转移，使之在每一个温度下达到热平衡，则全局最优解将以概率1被找到。因此可以说模拟退火算法可以找到全局最优解。

2 滤波算法比较

本节中介绍几种常用的滤波方法，它们各有长处，同时也有一定的缺点。

中位值滤波法[2]：连续采样N次（N次取基数）如图1，将N个值按大小排列，取出中间值P替代原像素值[3]。能有效克服因为偶然因素引起的波动干扰，对温度，液位的变化缓慢的被测参数有良好的滤波效果，但是对流量、速度等快速变化的参数不宜。采样序列如图1所示。

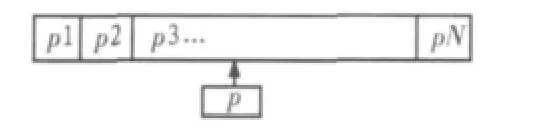
图1 采样序列Fig.1Sampling list

均值滤波[4]：实际上是用均值替代原图像中的各个像素值。均值滤波的方法，对将处理的当前像素，选择一个模板，该模板为其邻近的若干像素组成，用模板中像素均值来替代原像素的值。如图2所示，序号为0是当前像素，序号为1至8是邻近像素。求模板中所有像素的均值，再把该均值赋予当前像素点（x，y），作为处理后图像在该点上的灰度g（x，y），即：

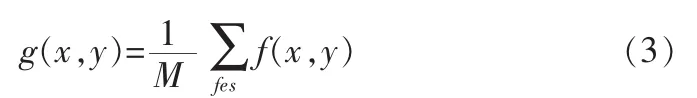
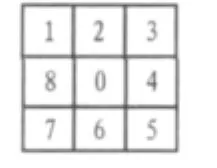
图2 像素模板Fig.2Pixel template

方差：是实际值与期望值之差平方的平均值，用公式D（x）=E{[X－E（X）]2}表示。方差刻画了随机变量的取值对于其数学期望的离散程度。

若X的取值比较集中，则方差D（x）较小；

若X的取值比较分散，则方差D（x）较大。

因此，D（x）是刻画X取值分散程度的一个量，它是衡量X取值分散程度的一个尺度。

基于模拟退火的滤波算法集合以上各种算法的优点，综合了中值滤波和均值滤波的长处，可以自适应的处理图像内部和图像边缘的噪声处理[5]。利用机率函数有机率的接受较差的扰动解为新解，使其避免传统梯度搜寻法（Gradient Search）往往陷入区域解的缺点，当在图像内部时，模拟退火会搜索到中值的附件进行选择，同时又会以一定的概率接受中值附件的值，同时又以一定的比例与其他点进行加权，综合了周围点的信息。当在图像边缘时，会从图像的4个方向水平方向，垂直方向，左下到右上方向和左上到右下方向，如图3所示。进行搜索，这样可以找出图像的梯度变化方向，找到图像的变化规律，找到适合的点替代当前噪声点，从而去除噪声。

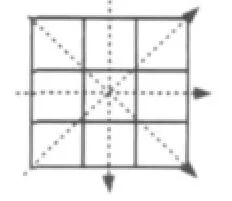
图3 搜索方向Fig.3Search direction

3 基于模拟退火的滤波算法

3．1 算法基本原理

基于模拟退火的滤波算法是基于下面的原理：对于一个含噪声的图像的每个像素点都以其中心选取一个的正方形领域如图2，利用方差表现了离散值的分布情况特点，首先对领域范围内的值求出期望和方差，找出领域值的分布情况，如果方差值比较小，则说明领域值分布比较集中，同时也说明噪声在图像内部，更偏向于使用中值滤波，如果方差值比较大，则说明领域值分布比较分散，图像信息变化比较快，说明噪声在图像的边缘地带，更应偏向使用加权平均滤波。然后使用模拟退火算法对领域范围内的值，进行概率搜索，如果方差值比较大，则在退火过程中退火温度设置较高，这样便于查找出偏离中值的值，能够更试用于图像变化比较明显的地方；如果方差值比较小，则在退火温度设置较低，便于查找到中值附近，这样更适用于在图像内部进行去除噪声。然后将查找出的值与剩下的值采样一定比例进行信息融合，如果在图像内部采用9.5：0.5的比例，在图像边缘采样8：2的比例。将信息融合后的值代替当前图像值。

3．2 实现步骤

1）为图像的目标像素设置一个3×3模板，该模板包括了其周围的邻近像素；

2）求出模板邻域范围内的值的期望E和方差D，根据方差设置冷却温度T0；

3）利用模拟退火算法为模板内的值进行退火求解。

①初始化：初始温度T（足够大），初始解的状态S（是算法迭代的起点），每个T值的迭代次数L；

②对k=1，……，L做第③至第⑥步；

③产生新解S’；

④计算增量Δt’=C（S’）－C（S），其中C（S）为评价函数；

⑤若Δt’＜0则接受S′作为新的当前解，否则以概率exp（－Δt’/T）接受S’作为新的当前解；

⑥如果满足终止条件则输出当前解作为最优解S’，结束程序；

终止条件取为当前点接近期望值和冷却温度的满足，则终止算法；

4）将3中求出的最优解Xk与其他点进行加权运算，最优解的值x的权为α，其他的值的权相同并且和为1－α，

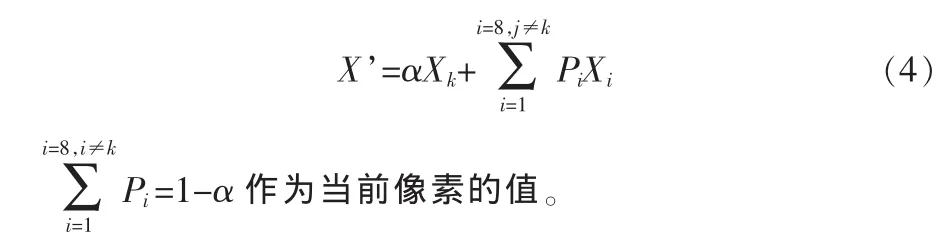
解空间：每个目标像素的领域的解空间为模板周围的8个临近像素值

S={P0P1…P8|Pi∈当前模板}

目标函数：设置目标函数为

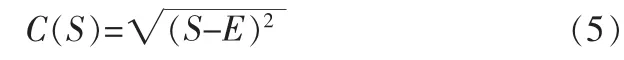
其中E为模板内值的期望值，表示当前值S偏离期望值E的距离。

初始解：如果方差较小，从方阵的左上角开始搜索，新解为顺序搜索模板内下一个值；

如果方差较大，解的搜索范围分为4个方向：水平方向，垂直方向，左下到右上方向和坐上到右下方向。从方阵的以上4个方向顺序进行搜索，比较4个方向与期望的绝对差值，选择差值较小的方向开始搜索，再向着偏离期望较远的方向进行搜索。

目标函数差：Δt’=C（S’）－C（S）

算法流程图如图4所示。

图4 算法流程Fig.4Flow chart of program algorithm

3.3 算法讨论分析

模拟退火算法具有概率演变[6]的特点，能够快速的收敛并达到最优值，这让模拟退火算法被广泛使用。但是它的参数可控性却是使用的难题。在这里讨论下模拟退火滤波算法中参数的设置问题。

1）根据模板方差判断是在图像内部还是边缘处

因为在图像内部像素的差别比较小，分布比较均匀，故方差较小；在图像的边缘处，像素变化比较明显，分布比较散开，故方差较大。在本算法中方差值的判断阀值一般为：D（x）＞0.3为图像边缘处，D（x）＜0.3时当着图像内部处理。

2）温度T的初始设置和温度下降速度和冷却温度

初始温度是影响模拟退火算法的一个重要因素，适当大的温度可以保证算法在全局范围进行搜索，找到全局最优解，但可能因为过大而浪费时间，所以本算法为解决速度问题，提出了当温度较高时候可以加快温度下降速度，设温度下降函数为Temp=Temp*y（y约0.8～0.99为佳）。当模板方差较大时，在图像内部时候，为求出接近中值的解，故冷却温度较低；当在图像边缘时候，为求出适合图像变化方向的值，故而使用了基于方向的梯度方向搜索和冷却温度较高。

4 实验结果与结论分析

在256×256的灰度图像中加入随机均匀的多种噪声，然后分别用中值滤波，均匀滤波和本算法滤波进行处理，处理结果下图可知：均值算法会丢失图像细节信息，产生模糊；中值算法虽然对图像细节信息保留较好，但是去燥不是很好；本算法结合两者的优点，在既较好的保留图像信息的同时，又有较好的去燥能力。

图5 原图Fig.5Original drawing

图6 加入椒盐噪声图Fig.6Salt-and pepper noise drawing

图7 均值滤波图Fig.7Mean filter drawing

图8 中值滤波图Fig.8Median filter drawing

本算法分析并结合传统滤波算法的优缺点，提出了一种基于模拟退火[7]的图像滤波算法，可以自适应的对图像内部和图像边缘进行分类处理，以一定的概率接受偏离中值的像素，再结合了加权平均的处理，综合了中值滤波和均值滤波的优点，该算法在有效过滤噪声的同时较好的保存了原始图像的信息。

[1]Eng H L，Ma K K.Noise adaptive soft-switchingn median filter[J].IEEE Trans Image Processing，2001，10（2）:240-260.

[2]Chan R H，Ho C-W，Nikolova M.Salt-and-pepper noise removal by median-type noise detectors and detail-preserving regularization[J].IEEE Trans Image Processing，2005，14（10）:1479-1485.

[3]王章伟，郑昌琼，王景熙，等.一种新型自适应中值滤波器在超声医学图像中的应用[J].四川大学学报。2000，32（5）：92-95.WANG Zhang-wei，ZHENG Chang-qiong，WANG Jing-xi，et al.Application of a new self-adaptive median filter in medical ultrasonic images processing[J].Journal of Sichuan University.2000，32（5）:92-95.

[4]邢文训，谢金星，现代优化算法[M].北京：清华大学出版社，2003：80-130.

[5]杨欣，费树岷，陈丽娟.基于模拟退火的寻找给定压缩图像的最优小波算法[J]，电子测量与仪器学报，2006（12）:64-66.YANG Xin，FEI Shu-ming，CHEN Li-juan.A new method of how to find optimal wavelet for given compressed image based on simulated annealing[J].Journal of Electronic Measurement and Instrument.2006（12）:64-66.

[6]潘梅森，易明，一种基于人类视觉的自适应均值滤波算法[J].计算机工程与应用，2006，39（10）：62-64.PAN Mei-sen，YI Ming.An adaptive mean filter algorithm based on HVS[J].Computer Engineering and Applications，2006，39（10）：62-64.