高阶IIR滤波器的FPGA实现

曾菊容

（宜宾学院物理与电子工程学院，四川宜宾644000）

数字滤波器是数字信号处理中最为广泛使用的一种基本线性处理模块，其功能本质上是将一组输入的序列通过一定的运算后转化为另一组数字序列。它可以实现模拟器件很难达到的准确线性相位特性。其实现方法主要有有限冲击响应数字滤波器（Finite Impulse Response，FIR）和无限冲击响应数字滤波器（Infinite Impuse Response，IIR）两种。在相同技术指标下，与FIR滤波器相比，IIR滤波器可以用较少的阶数来满足指标的要求，这是因为IIR滤波器引入了反馈机制，并且能够取得比较好的通带和阻带衰减特性。本文以实现的滤波器速度要快和硬件规模要小的目标来讨论了高阶IIR滤波器的FPGA实现。

1 IIR滤波器的基本结构

直接型结构的优点是简单直观，所使用的延时器数量少。缺点是改变某一个系数{ak}将影响所有的极点，改变某一个系数{bk}将影响所有的零点。更严重的是这种结构的极点位置灵敏度太大，对有限字长效应太敏感，容易出现不稳定现象和产生较大误差。对于三阶以上的高阶IIR滤波器，几乎不采用直接型结构，而是采用级联型、并联型等其他形式的结构。

级联型结构的一个重要优点是存储单元需要较少，硬件实现时，可以用一个二阶节进行时分复用。级联型结构的另一个特点是每一个基本节系数变化只影响该子系统的零极点，因此便于准确地实现滤波器的零、极点，也便于调整滤波器的频率特性。此外，级联型结构对系数变化的敏感度小，受有限字长的影响比直接型低，而且改变每一个二阶节级联的先后顺序，可以使滤波器特性得到优化，运算误差最小。

并联型结构运算速度快，各基本节的误差互不影响，还可以单独调整极点的位置，但不能像级联型那样直接调整零点，因为子系统零点不是整个系统的零点。因此，当要求准确传输零点时，以级联型为宜。综合考虑以上3种结构形式的优缺点，本论文采用级联结构形式。图2为高阶IIR滤波器的二阶节级联形式。

2 分布式算法IIR滤波器的设计[4，6]

因为数字滤波器涉及到大量的卷积运算，所以在使用硬件实现时将会占用大量的资源。为了避免这种情况的实现，可以利用FPGA芯片所具有的查找表结构，将卷积运算转化为查表移位求和运算。该算法结构有串行和并行两种，串行结构处理速度慢，并行结构处理速度快，但是硬件规模增大了，它是以增加额外的LUT、寄存器和加法器为代价来提高速度的。本论文对两种结构方式进行这种，提出一种串并结合的分布式算法，其基本思路是将输入数据分段，各小段再查表移位相加，这些小段的处理是并行的，可提高运算速度，然后再将小段运算后的部分和再移位相加。其具体结构如图3所示，该图为一个基本二阶节DA算法结构，其中输入信号和反馈信号具有同样数据宽度，均为16位。图中，DAl，DAll是4位DA算法模块，其中DAll是最高4位DA算法模块，DA2是高4位和低4位DA结果相加模块，DA3为高8位和低8位DA结果相加模块，加法器是将输入部分和反馈部分计算结果相加。

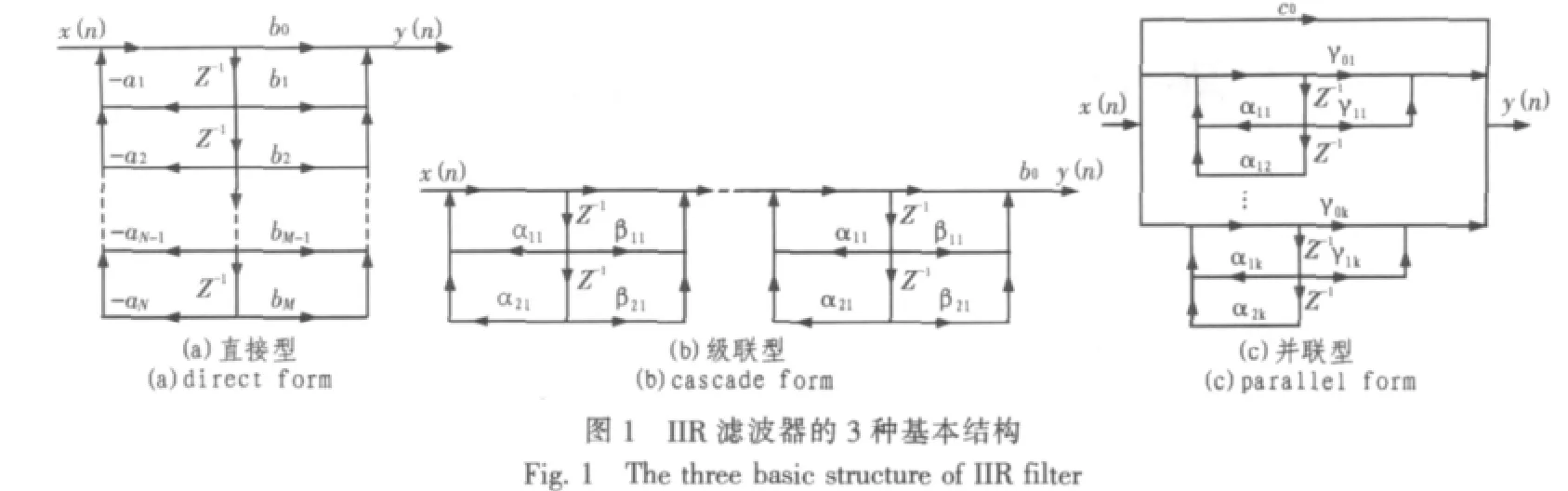
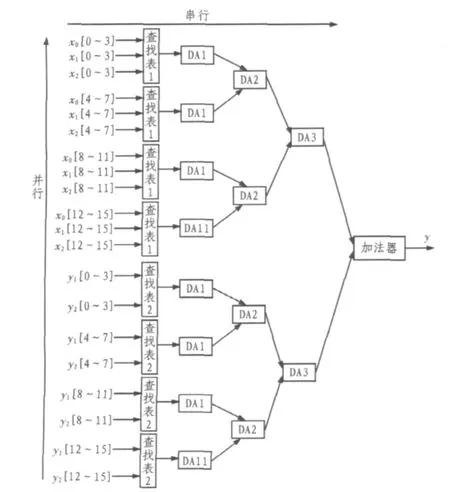
图3 基本二阶节串并结合的DA算法结构Fig.3DA arithmetic structure combined the cascade and parallel for the basic 2 order

3 IIR滤波器的设计、仿真与测试

3.1 IIR滤波器的设计

本文设计的IIR滤波器抽样率为Fs=10 MHz的低通滤波器，其通带截止频率Fp=500 kHz，阻带截止频率Fs=550 kHz，通带最大衰减Ap=0.1 dB，阻带最小衰减Ap=60 dB。由于椭圆型滤波器相比巴特沃斯型和切比雪夫型实现时所需要的阶数最少，所以文中采用椭圆型滤波器来实现。利用Matlab软件计算系统函数，先利用函数ellipord（Wp，Ws，Rp，Rs）计算出椭圆滤波器的阶数N和3 dB截止频率Wn，再利用函数ellip（N，Rp，Rs，Wn）可以求得直接型椭圆IIR滤波器的各个系数。通过调用以上两个函数计算得到的传递函数H（Z）为[2]：

由传递函数可见这是一个10阶IIR滤波系统。借助Matlab信号处理工具箱中函数tf2sos可实现将传递函数转换为二阶节级联形式。

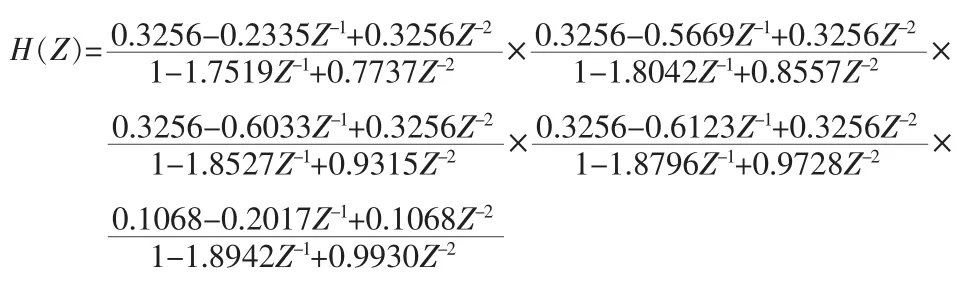
3.2 传递函数系数的量化处理

数字滤波器在硬件实现时，需要把由理论设计出的理想数字滤波器传递函数的各系数加以量化。由传递函数可以知道，系数直接决定了零、极点的位置，并且极点的位置对系统特性影响最大。由于系数的量化，使系统函数的零、极点会偏离原来的准确位置。这样实际的传递函数将与原来设计的有所不同，也就是系统的实际频率响应与设计的滤波器的频率响应有偏离，如果系数量化使零、极点的移动太大，就会使滤波器的性能指标达不到设计的技术要求。甚至可能使原来在单位圆内的极点移至单位圆外，稳定系统成为不稳定系统。

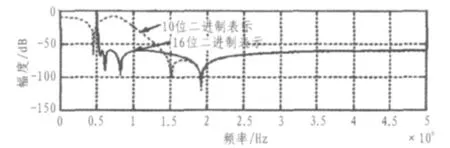
图4 滤波器系数量化前后的幅频特性Fig.4Amplitude frequency characteristic of filter coefficient before and after quantification

图4比较了在本设计中系数用不同位数的二进制数表示的幅频特性仿真图，其中用虚线表示的曲线是系数用10位二进制数表示的系统的幅频特性，用实线表示的曲线是系数用16位二进制数表示的系统的幅频特性和理论计算出的幅频特性（二者基本重合在一起）。通过仿真图可以看出用10位二进制数对系数进行量化后幅频特性曲线严重偏离理论设计值，而16位二进制数量化则基本与理论计算出的幅频特性曲线重合，能达到预定的指标。通过讨论系数的量化误差对极点位置的影响，本文确定滤波器系数的数据位数为16位，精度14位，输入数据宽度为12位符号数，反馈数据宽度为16位，输出数据宽度为14位。

3.3 IIR滤波器的QuartusⅡ仿真[3，5]

设计中采用了原理图输入方式和文本输入方式，在QuartusⅡ中完成了上述10阶IIR滤波器的设计，为了检测该滤波器是否正确工作，手动输入周期数据（10个-511，10个511），相当于周期方波信号（频率为500 kHz，采样率为10 MHz）一个周期的采样数据，Matlab的计算值与QuartusⅡ的仿真值如表1所示。由信号理论分析可知，周期方波信号没有偶次谐波，所以对三次及以上的谐波衰减经过IIR滤波器后输出仅有基波（频率为500 kHz）正弦信号，理论计算给出的方波周期信号基波幅度650.95，由表1可见，Matlab软件计算出的基波幅度为：（625.7-（-663.4））/2=644.55，与理论值的误差为：（644.55-650.95）/650.95=-0.98%，QuartusⅡ软件仿真输出的基波幅度为：（600-（-652））/2=626，与理论值的误差为：（626-650.95）/650.95=-3.83%，仿真值与理论值误差较大是由于有限精度算法所引起的误差，可以通过增加二进制位数来提高系统的精度。

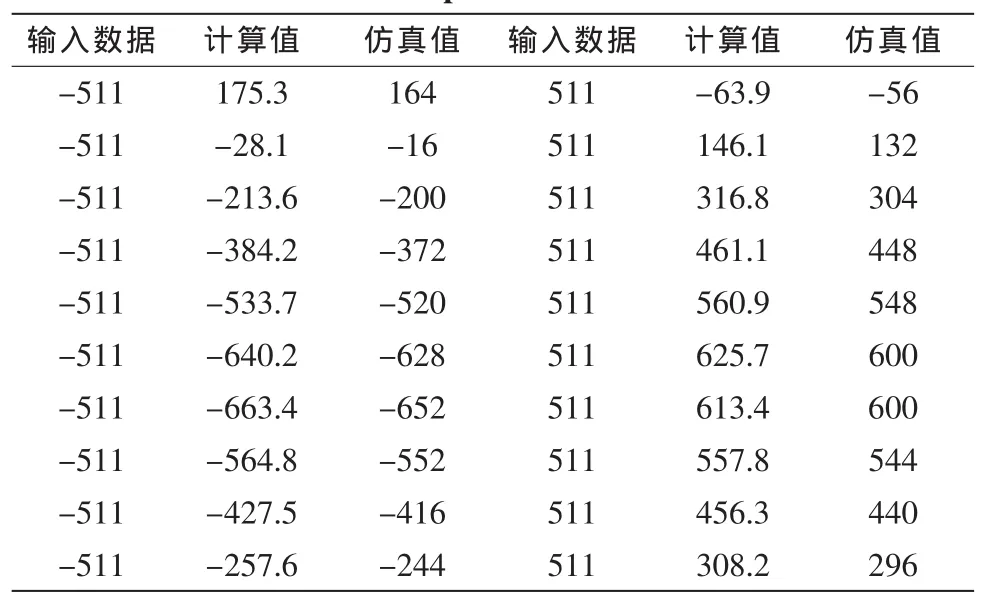
表1 滤波后输出的数据Tab.1Output data after filter

3.4 IIR滤波器的硬件测试

测试系统包括了3个部分：信源、实验电路和示波器。信源可由信号发生器提供，本次实验中是通过对系统时钟分频得到的周期方波信号，因为周期方波信号含有丰富的谐波分量，便于用FFT图观测。实验电路主要包括A/D转换电路、IIR滤波器和D/A转换电路。在实验电路中，输入的信号先经过A／D转换电路，转换后的数字信号送入用FPGA实现的IIR滤波器电路进行滤波处理，滤波后的数据仍然是数字信号，因此再通过A／D转换电路将其还原为模拟信号。测试中采用双踪数字示波器DSll02C来观测滤波前后的结果。测试结果如图6所示。

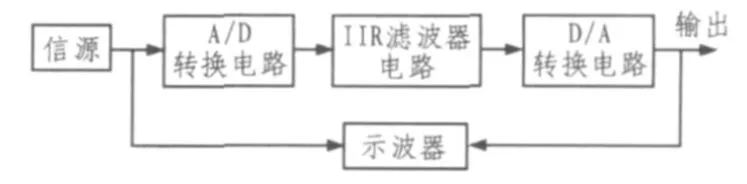
图5 测试系统组成框图Fig.5The block diagram of test system

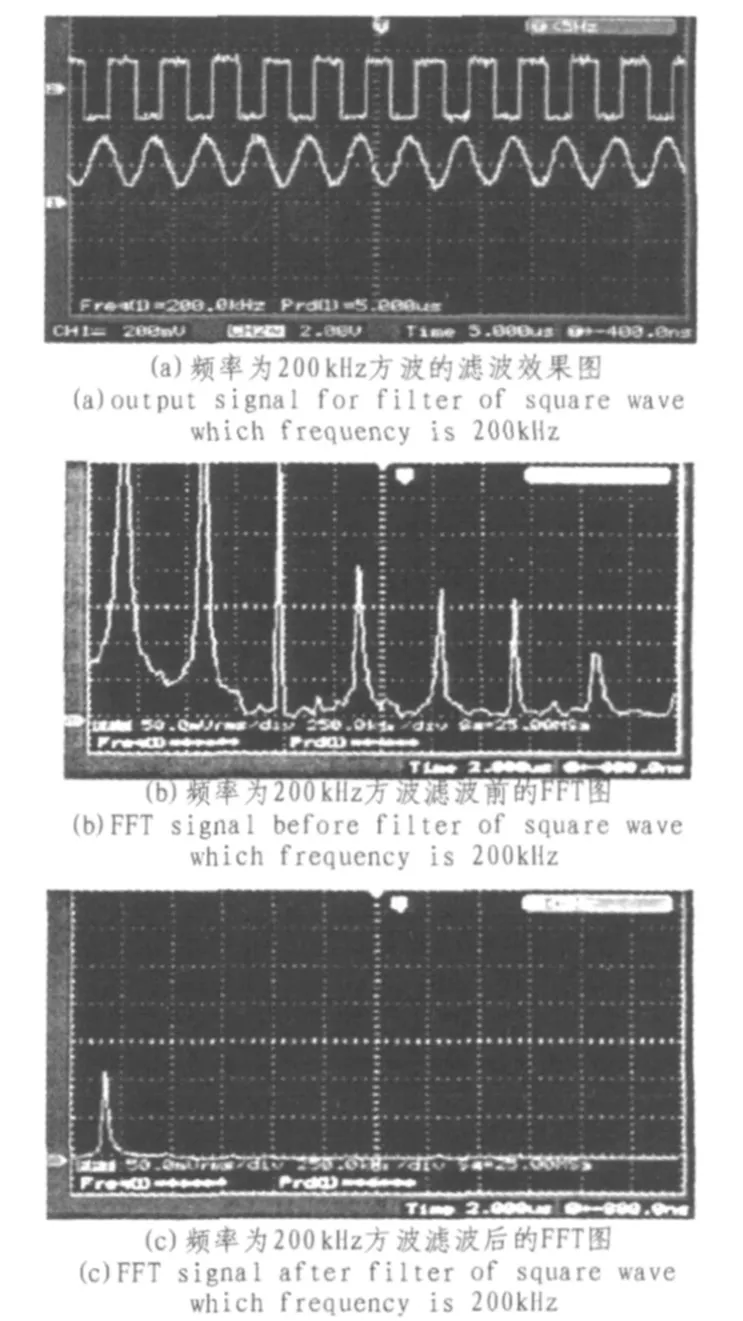
图6 频率为200 kHz方波滤波前后的效果图Fig.6The signal before and after filter of square wave which frequency is 200 kHz

由信号理论分析可知，周期方波信号不含有偶次谐波，又由于所设计低通滤波器的通带截止频率为500 kHz，所以当输入为200 kHz时，高次谐波都被滤除了，只剩下基波，测试结果与理论分析一致。

4 结论

本文完成了基于FPGA的高阶IIR滤波器的设计与实现。首先结合IIR滤波器的基本结构，针对分布式算法中查找表规模过大的缺点，采用级联或并联结构，利用多块查找表使得硬件规模极大地减小，提出了并行和串行相结合的设计方案，然后在QuartusⅡ软件平台上，对设计的滤波器进行了仿真验证，然后对Matlab理论值和仿真值进行了比较分析，验证了设计的IIR滤波器的正确性。最后还做了硬件测试，测试结果表明，本文所设计的滤波器硬件规模较小，系统最高时钟频率达到了80 MHz以上，体现了设计的实时性。同时，只要将查找表进行相应的改动，就能分别实现低通、高通、带通IIR滤波器，体现了设计的灵活性。

[1]胡广书．数字信号处理——理论、算法与实现[M]．北京：清华大学出版社，2003．

[2]赵红怡，张常年．数字信号处理及其MATLAB实现[M]．北京：化学工业出版社，2002．

[3]邹彦，庄严.EDA技术与数字系统设计[M].北京：电子工业出版社，2008.

[4]黄晓红，蔡江利.基于FPGA的改进型FIR滤波器的实现[J].电子技术应用，2009（5）：32－34.HUANG Xiao-hong，CAI Jiang-li.Design of improved FIR filter based on FPGA[J].Application of Electronic Technique，2009（5）：32－34.

[5]屈星，唐宁，等．基于FPGA的IIR数字滤波器的设计与仿真[J]．计算机仿真，2009，26（8）:304－307.QU Xing，TANG Ning et al.Design of IIR digital filter based on FPGA[J].Computer Simulate，2009，26（8）:304－307.

[6]魏灵，杨日杰，等.基于分布式算法的数字滤波器设计[J].仪器仪表学报，2008，29（10）:2100－2104.WEI Ling，YANG Ri-jie，et al.Design of FIR filter based on distributedarithmeticanditsFPGAimplementation[J].Chinese Journal of ScientificInstrument，2008，29（10）:2100－2104.