软件可靠性多模型综合预测研究综述

王二威，崔春生，田艳

（1.北京理工大学珠海学院管理与经济学院，广东珠海519085；2.河南财经政法大学计算机学院，河南郑州450002）

随着计算机软件进入越来越多的领域，软件可靠性问题已经引起了人们的普遍重视，软件可靠性的研究也成为人们关注的焦点。到目前为止软件可靠性模型的研究取得了很大的成果，提出了近百种软件可靠性模型，如JM模型、GO模型等，这里称此类模型为经典模型。由于这些模型在对软件可靠性进行评估时根据开发环境等做了很多的假设，而软件在实际运行时却受到各种随机因素的综合作用，使得软件的故障多种多样，情况比较复杂。用一些固定的假设去套用各种各样的软件环境，显然是不合适的；而针对每一种情况都去开发一个新的模型既费时又费力[1]。

软件可靠性研究发展到90年代，人们在经典模型的基础上将更新的理论如：神经网络、贝叶斯网络、遗传算法、支持向量机、混沌理论、泛函网络等应用于软件可靠性建模和优化，产生了许多新的预测方法。由于神经网络能够从背景不清楚和不完全的数据中自动提取反映事物内在规律和特点的知识，并能够应用通过学习所获取的知识来进行问题的求解，比较多的研究者关注于基于神经网络的方法[2-6]。基于神经网络的软件可靠性模型可以对不同数据不同复杂情况有针对性地构建模型，通过训练确定参数；但它不能很直观的去解释网络权重[2]，且网络结构、归一化方法、激励函数都会对模型预测性能产生很大的影响，Cai[6]就在大量对比实验的基础上指出，大多数情况下基于神经网络的方法很难得出满意的量化预测结果。

由于单个经典模型的局限性以及基于新理论方法的复杂性和不成熟性，软件可靠性预测仍然还有很多问题需要解决：一是建立能够普遍应用的模型，二是设计一套行之有效的模型选择方法，能够让工程人员从众多的软件可靠性模型中选择出最适合实施项目的模型。

Bev Littlewood在对大量软件项目研究的基础上提出了“变点”的思想[7]，表明不能期望用某一个模型来描述软件的失效过程，而从另一个侧面表明可以用多个模型来描述软件的失效过程。香港中文大学的Michael Lyu首先提出多模型综合预测的思想[8]，即：专注于将已有的经典软件可靠性模型充分有效的利用起来，将多个单一的经典模型的预测优势“综合”起来。他在实验的基础上提出多模型综合一般比单个经典模型的预测效果更好，精度更高，而且抗数据“噪声”能力强，不但对短期预测有效，长期预测效果更为明显。而这正是现实软件工程所需要的，也是发展的一个趋势。

1 软件可靠性多模型综合预测方法

从文献分析中可以看出，从Lyu首次提出多模型综合的思想以后，先后出现了十多种综合预测模型，大致分为3类：Lyu的线性综合模型，基于神经网络的预测模型以及其他。

1.1 Lyu的线性综合模型

Lyu在其文章[8]中首先提出了更有效地利用现有的经典模型，将多个模型综合起来进行软件可靠性的分析。首先根据软件测试运行环境从经典模型中确定一个基本的模型集；然后从模型集中选择那些预测的偏好可以相互抵消的模型，并分别用选定的单个模型进行软件可靠性的预测；最后确定一些准则对选定的模型分别赋予不同的权重从而形成一个线性的综合模型。Lyu给出了综合模型的一般表达式：

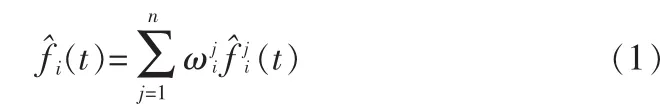
Lyu的线性综合模型具有很重要的意义，它提供了研究软件可靠性的一种新的思路，即是每个单一经典模型都有很大的局限而且精度也不够高，那么就把这些经典模型综合起来，以更有效的应用这些经典模型，进而取得更好的预测效果。试验证明这种方法有很好的预测效果，有很光明的应用前景。

1.2 基于神经网络的预测模型

此类预测模型[9-14]充分利用神经网络的自适应、自学习能力，以几个经典模型的预测值作为神经网络的输入，以实际值作为输出，构建网络结构，然后利用历史数据对网络进行训练以确定网络权重，建立预测模型。

基于神经网络的预测模型有3个明显的问题：1）神经网络结构的确定往往需要大量训练，每一个软件项目可能会需要不同结构的神经网络，而直接确定网络的结构则太主观；2）神经网络权重缺乏解释性；3）经典模型的选择比较主观。

1.3 其他

邹丰忠等人提出用贝叶斯方法[15-17]实现多模型的自动混合、自动选择，用贝叶斯理论进行权值的计算，将权值作为贝叶斯超参数，根据实际数据进行超参数更新，实现多模型的综合预测。马飒飒等人提出了基于模型聚类的多模型综合预测方法[18]，其基本思想是：具有相似性的失效数据适用于同一软件可靠性模型。原菊梅[19]等运用包含度理论动态确定权重来进行预测。各类综合模型的比较分析如表1所示。

2 软件可靠性多模型综合预测研究框架

软件可靠性多模型综合预测研究框架如图1所示。

首先是经典模型的选择，找到科学合理的选择准则体系是该阶段的关键。其次是单个经典模型权重的确定，即是找到在不同时期哪些经典模型有更好的预测效果，对整个综合模型的贡献最大，该阶段是多模型综合的核心。文献中出现的综合模型的核心和不同之处皆在于此，通过各种理论、工具和算法来精确有效的确定权重。再次是将选择的单个经典模型组合起来建立综合模型，包括线性综合和非线性的综合。线性综合模型构建简单快速，而且预测精度比单个经典模型要好；非线性综合模型构建复杂，需要进行大量训练，但是可能获得较高的预测精度。可以根据软件工程的实际需求，对于预测精度要求不是很高的可以采用线性综合模型，对于预测精度要求较高的可以采用线性和非线性综合相结合的方式进行预测。最后是建立合理的评价准则对综合模型的预测性能进行评价。现有的评价准则比较单一，如平均误差（AE：average error）[20]、平均偏差（AB：average bias error）[20]、均方根误差（RMSE：root mean square error）[8]等，有待形成一套评价体系以便从各个方面考察综合模型的预测性能。

表1 各类综合模型的比较分析Tab.1Comparison of different combational models

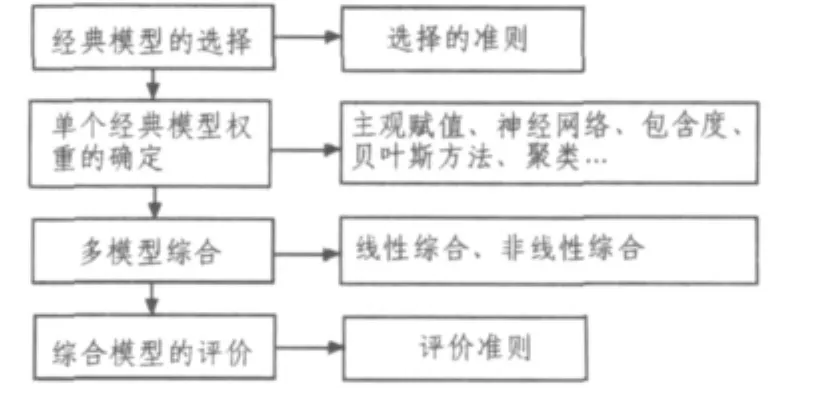
图1 软件可靠性多模型综合预测研究框架Fig.1Research framework of multi-model for software reliability prediction

从现有文献分析可以看出，已有的研究比较注重采用各种方法来确定单个模型的权重[8-19]，多模型综合多为线性综合[8-9，15-19]，对非线性综合研究的比较少[11-13]；另外对经典模型的选择准则和综合模型的评价准则只是进行了一些简单的说明，缺乏比较系统的研究；实际上，经典模型是多模型综合的基础，经典模型的选择在构建综合模型过程中是至关重要的，需要进行比较深入、系统的探讨和研究。

3 结论

基于“综合”的思想，对文献中软件可靠性多模型综合预测方法进行了梳理，大致分为3类：Lyu的线性综合模型简单有效且具有普适性，但是单个经典模型权重的确定比较主观；基于神经网络的模型，网络结构的构建比较主观，网络权重缺乏解释性，普适性较差；其他模型中或者理论性较强，缺乏数据论证，或基于一定的假设条件。在对比分析的基础上提出了软件可靠性多模型“综合”预测的研究框架，包括模型选择、单个经典模型权重确定、多模型综合、模型评价4个阶段，其中单个经典模型权重的确定和线性综合是当前研究的热点，非线性综合以及经典模型的选择准则有待进一步深入系统的研究。

[1]徐仁佐.软件可靠性工程[M].北京:清华大学出版社，2007.

[2]Karunanithi N，Whitley D，Malaiya Y K.Prediction of software reliability using connectionist models[J].IEEE Transactions on Software Engineering，1992，18（7）:563-574.

[3]Khoshgoftaar T M，Szabo R M.Using neural networks to predict software faults during testing[J].IEEE Trasactions on Reliability，1996，45（3）:456-462.

[4]Sherer S A.Software fault prediction[J].Journal of System and Software，1995，29（2）:97-105.

[5]Sitte R.Compareson of software-reliability-growth predictions:neural networks vs parametric-recalibration[J].IEEE Trasactions on Reliability，1999，48（3）:285-291.

[6]Cai K Y，CAI Lin，WANG Wei-dong，et al.On the neural network approach in software reliability modeling[J].The Journal of Systems and Software，2001，58（1）:47-62.

[7]Phame H.Reliability handbook[S].NewYork:Springer Verlag，2002.

[8]Lyu M R，Nikora A.Applying reliability models more effectively[J].IEEE Software，1992，9（4）:43-52.

[9]吴勤，侯朝桢，原梅菊.软件可靠性多模型综合的预测方法[J]，计算机工程，2006，32（23）:214-215.WU Qin，HOU Chao-zhen，YUAN Mei-ju.Multi-model prediction method for software reliability[J].Computer Engineering，2006，32（23）:214-215.

[10]张雪松，郭平.基于组合神经网络的软件可靠性预测研究[J].北京师范大学学报：自然科学版，2005，41（6）：599-603.ZHANG Xue-song，GUO Ping.A study on software reliability prediction based on ensemble neural network[J].Journal of Beijing Normal University：Natural Science，2005，41（6）：599-603.

[11]尹乾.基于神经网络的软件可靠性模型研究[D].北京:北京师范大学，2006.

[12]SU Yu-shen，HUANG Chin-yu，CHEN Yi-shin，et al.An artificial neural-network-based approach to software reliability assessment[J].Tencon 2005 IEEE，2005（10）:1-6.

[13]SU Yu-shen，HUANG Chin-yu.Neural-network-based approaches for software reliability estimation using dynamic weighted combinational models[J].Journal of Systems and Software，2007，80（4）:606-615.

[14]王高祖，李伟华，徐艳玲.基于神经网络组合模型的软件可靠性评估研究[J].计算机仿真，2010，27（8）:176-180.WANG Gao-zu，LI Wei-hua，XU Yan-ling.Research of softwarereliabilityassessmentbasedonneuralnet combinational model[J].Computer Simulation，2010，27（8）:176-180.

[15]邹丰忠，徐仁佐.软件可靠性多模型综合评估[J].同济大学学报，2002，30（10）：1183-1185.ZOU Feng-zhong，XU Ren-zuo.Multi-model assessment of software reliability[J].Journal of Tongji University，2002，30（10）：1183-1185.

[16]邹丰忠，刘海青，王林.软件可靠性综合模型[J].武汉大学学报：工学版，2003，36（1）：86-88.ZOU Feng-zhong，LIU Hai-qing，WANG Lin.Integrated model of software reliability[J].Journal of Wuhan University of Hydraulic and Electric Engineering，2003，36（1）：86-88.

[17]马飒飒，宁如云.基于贝叶斯估计的软件可靠性综合评估模型[J]，兵工学报，2008，29（4）:440-445.MA Sa-sa，NING Ru-yun.Software reliability integrated evaluation model based on Bayesian estimation[J].Acta Armamentarili，2008，29（4）:440-445.

[18]马飒飒，陈自力，赵守伟.软件可靠性及可靠性多模型综合研究[J]，微计算机信息，2006，22（6-3）:263-265.MASa-sa，CHENZi-li，ZHAOShou-wei.Integrated research on software reliability and reliability multi-models[J].Contral and Automation，2006，22（6-3）:263-265.

[19]原菊梅，侯朝桢，王小艺，等.基于包含度理论的软件可靠性多模型综合动态预计[J].计算机应用，2007，27（2）：387-393.YUAN Ju-mei，HOU Chao-zhen，WANG Xiao-yi，et al.Multi-modelsynthesisdynamicpredictionofsoftware reliability based in inclusion degree theory[J].Journal of Computer Applications，2007，27（2）：387-393.

[20]Malaiya Y K，Karunanithi N.Predictability measures for softwarereliabilitymodels[C]//FourteenthAnnualInternational ComputerSoftwareandApplicationsCoference，Chicago1990:7-12.