一个新的自认证聚合签名方案

葛荣亮，高德智，梁景玲，张云

（山东科技大学信息科学与工程学院，山东青岛266510）

传统的公钥密码系统需要管理用户的证书，在管理证书的过程中需要大量的计算和存储开销。为此，1984年Shamir[1]首先提出了关于身份的数字签名的构想。这个方案简化了证书管理的过程，但是存在着密钥托管问题和安全信道的问题。

1991年Girault[2]提出了自认证公钥（SCK）的概念，这篇文章结合了基于身份的概念和传统PKI应用的概念。1997年Petersen和Hoster[3]扩展了Girault的方法写了一篇关于自认证密钥概念和应用的文章。2001年Shao[4]提出了基于自认证公钥的加密系统，但这篇文章缺少安全模型与安全证明。2002年Lee[5]提出了一个自认证的签名方案，但是这个方案不安全。后来又有一些方案相继被提了出来，2007年Shao[6]提出了基于椭圆曲线上双线性对的自认证签名方案，在这个方案中，认证中心（CA）将部分私钥通过变换隐藏，然后发给用户，用户收到后首先恢复私钥，然后签名。相比于基于身份的签名方案，自认证方案能够很好的解决安全信道问题。

现在数字签名技术有了更为广泛的应用，但在一些特殊的环境中有限制，比如在传感器、手机、个人数字助理（PDA）中，当需要对多个签名同时验证的时候，就会产生突出的效率问题。为了应对这类问题。2003年Boneh[7]等人第一次提出了一个聚合签名方案，即将n个签名聚合成单一的签名。2004年，Cheon[8]等人提出了第一个基于身份的聚合签名方案，并指出不是所有的基于身份的签名方案都能变换成聚合签名方案。2007年，Gong[9]等人提出了基于双线性映射的两个无证书聚合签名方案，这两个方案可以用在不同的环境中。2010年孙华[10]等人提出了一种安全有效的基于身份的聚合签名方案，这个方案具有较高的效率。

本文提出了一个自认证聚合签名方案。该方案参考了文献[10]的签名方案，并加入自认证的过程，使方案具有更高的安全性，同时利用计算Diffie-Hellman问题的困难性，在随机预言模型下证明了方案的安全性。

1 预备知识

简要回顾双线性对的概念和一些相关的数学知识：

双线性对：令G1是阶为q的加法循环群，G2是阶为q的乘法循环群，P是G1的生成元，Z是阶为q的非零素域，令e：G1×G1→G2是满足下列条件的一个双线性映射：

1）双线性：对于任意P，Q∈G1，以及a，b∈Z，满足e（aP，bQ）=e（P，Q）ab；

2）非退化性：存在P，Q∈G1，满足e（P，Q）≠1；

3）可计算性：对于任意P，Q∈G1，存在一个有效的算法计算e（P，Q）。

在群G1上，可以定义以下几个密码学问题：

计算性Diffie-Hellman问题（CDHP）：对于任意a，b∈Z和P∈G1，已知（P，aP，bP），计算abP，如果离散对数问题可解，CDH问题可解，反之，不一定成立。

判定性Diffie-Hellman问题（DDHP）：给定P，aP，bP，cP对于a，b，c∈Z，判断c=ab（modq）是否成立。

双线性Diffie-Hellman问题（BDHP）：给定P，aP，bP，cP对于任意未知的a，b，c∈Z，计算e（P，P）abc。

Gap Diffie-Hellman问题（GDHP）：在多项式时间内，判断性Diffie-Hellman（DDHP）问题是可解的，而不存在多项式时间算法能以不可忽略的概率解决计算Diffie-Hellman（CDH）问题。任何多项式时间内算法A能够成功解决CDH问题的可能性定义为：Succ=Pr[A（P，aP，bP）=abP:a，b，c∈Z]。CDH问题假设对于每一个多项式时间内的算法，Succ可忽略。

2 一个自认证聚合签名方案

本方案一共包含6个算法，具体算法如下：

2.1 系统建立算法

认证中心（CA）完成以下步骤：

1）选取阶为q的加法循环群G1和乘法循环群G2，取群G1的两个生成元P和Q，设双线性对e：G1×G1→G2；

3）选取两个Hash函数：H1：{0，1}*×G1→G1，H2：{0，1}*×G1→，则系统参数为params={G1，G2，e，P，Q，Ppub，H1，H2}。

2.2 公钥生成算法

身份为IDi的第i个用户随机取xi∈Z*q作为秘密值，然后计算Pi=（Xi，Yi）用户公钥，其中Xi=xiP，Yi=xiPpub，那么任何人都可以通过检验等式e（Xi，Ppub）=e（Yi，P）是否成立来验证Pi的正确性。

2.3 部分私钥提取算法

第i个用户发送自己的身份IDi∈{0，1}*和公钥Pi给CA，然后CA计算局部私钥Di=sH1（IDi，Pi），s是CA的主密钥。CA取ki∈，计算Wi=kiP，Zi=Di+kiXi，然后CA（Wi，Zi）将通过公共渠道发给用户。

用户收到（Wi，Zi）后，首先恢复Di，即计算Di=Zi-xiWi，然后通过下面的式子

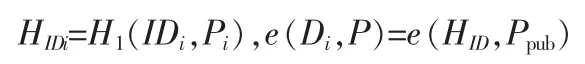
来验证Di的正确性。如果上式成立，则接受Di，否则拒绝。此时用户实际上拥有私钥（Di，xi）。事实上这里的Di是Boneh[11]等人提出的一个关于消息（IDi，Pi）的短签名。在上述过程中，认证中心（CA）将局部私钥隐藏在Zi，这样就可以把包含私钥的信息通过公共渠道发给用户。因此就能很好地解决安全信道的问题。

2.4 单个签名生成与验证算法

第i个用户，也即第i个签名者，收到认证中心（CA）传来的Di后，计算Si=xiDi作为自己的全私钥。

然后签名者对消息mi∈{0，1}*进行签名：

1）随机选取ri∈，计算Ui=riP；

2）计算hi=H2（mi，Ui）；

3）计算Vi=Si+riQ+hiDi，则消息mi上的签名是σi=（Ui，Vi）。

给定身份为IDi的签名者的公钥Pi，消息mi以及签名σi，就可以验证签名。首先，计算hi=H2（mi，Ui），di=H1（IDi，Pi），然后验证等式e（Vi，P）=e（di，Yi）e（Q，Ui）e（hidi，Ppub）是否成立，如果等式成立则σi是一个有效的签名。

2.5 聚合签名算法

这一阶段，任何人可以作为聚合签名的生成者，他可以将n个签名聚合成一个签名。假设U是签名者集合，S∈U为生成聚合签名者的集合，现设S中共有n个用户，他们的身份为ID1，ID2，…，IDn每个用户都有对消息mi的签名σi=（Ui，Vi）。那么聚合签名生成者在收到n个签名σi后，则产生的聚合签名是σ=（U1，…，Un，V）。

2.6 聚合签名验证算法

给定用户身份IDi，相应公钥Pi，消息mi，以及签名σ=（U1，…，Un，V），验证者执行以下步骤：

1）计算hi=H2（mi，Ui），di=H1（IDi，Pi），其中（i=1，…，n）；

3）如果等式成立，则σ是一个有效的聚合签名。下面是方案的正确性推导：

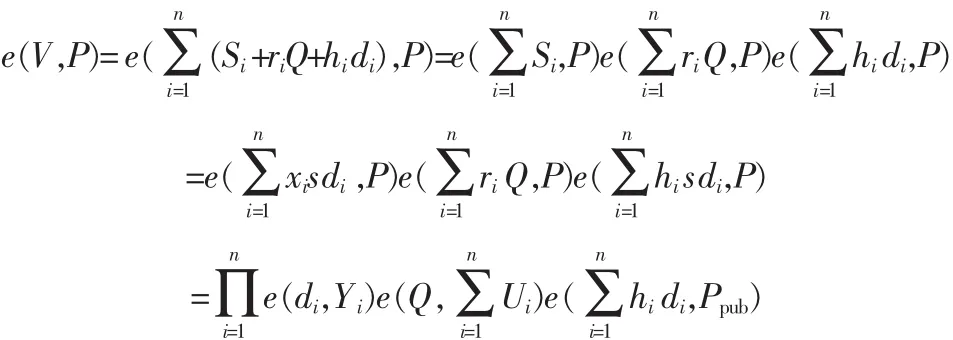
由此可得本方案是正确的。

3 安全模型与安全证明

首先给出安全模型，介绍第一类型的敌手和第二类型的敌手，接下来提供在随机预言模型下方案的安全性证明。

3.1 安全模型

在一个无证书的公钥密码学（CL-PKC）中存在着两种类型的攻击对手，分别是Type-1敌手和Type-2敌手。Type-1敌手A1不能获取CA的主密钥，但是他能替换个体的公钥。Type-2敌手A2能够获取CA主密钥，但是不能替换个体公钥。

这里可以把A1看作一般的适应性伪造者，而A2可以看作是不可信的CA或者是盗用主密钥的敌手。可以通过一个敌手A={A1，A2}和一个挑战者C之间的游戏定义聚合签名方案的安全模型。

1）系统建立：挑战者运行系统建立算法，获取系统参数params。然后对于Type-1敌手，挑战者自己保存主密钥。这里敌手先选取秘密值x*，计算相应的公后替换用户的公钥，C记录有效的替么对于身份为DID的用户，敌手询问用户的部分私钥DID，挑战者回复（W，Z），然后敌手就可以通过计算恢复DID。对于Type-2敌手，C直接告诉敌手主密钥。

2）询问：相对于身份ID为的用户，A向挑战者C提出任意信息的询问，C返回在用户公钥下的签名σ。

3）响应：A询问结束后，输出一个有效的聚合签名σ*，同时在这个过程中至少有一个消息mi上的签名σi，A是没有询问过的。那么，就认为敌手A获胜。定义A获胜的概率为A的优势，记为Adv（A）。

定义1一个敌手A以（t，N，ε，qH，qE，qs）攻破一个聚合签名方案，是指A的运行时间至多t，而且A进行了至多qH次Hash函数询问、qE次局部私钥询问、qs次签名询问，取得的Adv（A）至少为ε。而签名方案是（t，N，ε，qH，qE，qs）抗存在性伪造，是指不存在敌手A以（t，N，ε，qH，qE，qs）攻破聚合签名方案。

3.2 安全证明

假设CDH问题在随机预言模型下是困难的，下面将给出聚合签名方案的安全证明。

定理1如果存在一个Type-1敌手A以（t，N，ε，qp，qH，qE，qs）攻破聚合签名方案，那么就可以构造一个算法B在多项式时间内，以不可忽略的概率解决CDH问题。

证明：针对该方案，存在拥有最多ε优势和最多运行时间t的Type-1敌手A1，他以（t，ε）-攻破该方案。假设A1进行了至多qH次Hash函数询问、qp次公钥询问、qE次局部私钥询问、qs次签名询问。现设e是自然对数的底数，tG1为群中计算标量乘法所需时间，t是伪造的签名转化成CDH问题所需的时间。则存在（t*，ε*）的算法B以概率ε*≥ε/（qE+n）e，在时间t*≤φ（qH1，qH2，qE，qs，qP）tG1+t内解决CDH问题。

假设B构造了一个（P，aP，bP，abP）的CDH问题，现在要计算abP。

H1-Hash询问：A1做一个H1-Hash询问，B为了响应随机预言机H1的询问，维护一张五元组的列表L1:（IDi，Pi，wi，yi，zi），该表初始值为空，当敌手A1对IDi进行H1-Hash询问时，算法响应如下：

①如果IDi已经存在于L1中，B响应H1（IDi，Pi）=wi；

②否则B随机生成y∈{0，1}，令Pr（y=0）=δ，其中δ为某一概率值；

③B随机取z∈Z*q，如果y=0，B计算wi=z（bP）；若y=1，计算wi=zP；

④B把（IDi，Pi，wi，yi，z）加到列表L1中，并且返回给A1的值为H1（IDi，Pi）=wi。

H2-Hash询问：为了响应H2-Hash询问，算法B维护一张三元组的列表L2：（mi，Ui，ci），当敌手进行询问时算法B响应如下：

2）公钥询问：A1进行公钥询问，B响应如下：

①B维护一张列表L3：（IDi，Pi，xi），如果询问值已经存在，则返回Pi值；

②否则选取xi∈，计算Pi=（Xi，Yi）=（xiP，xiPpub），将（xi，Xi，Yi）添加到L3中，并返回Pi值。

3）公钥替换询问：A1为了获得新的公钥，进行公钥替换询问，B查找列表L3，如果存在则更新，否则进行一个公钥询问，然后更新。

4）部分私钥询问：A1进行部分私钥（IDi，Pi）询问，B响应如下：

①如果IDi，Pi以前被询问过，则B从L1中找出其值；

②否则B用IDi，Pi做H1-Hash询问；

③如果y=0，则B失败中止；否则，B计算Di=z（aP）。

5）签名询问：A1询问（IDi，Pi，mi）上的签名，B从L1中找到相应元组，然后执行以下步骤：

①如果y=0，则B失败，中止；

②否则表明H1（IDi，Pi）=ziP，B随机取ri∈，计算Ui=riPi；

③如果三元组（mi，Ui，ci）已在L2中，那么B取出ci，否则随机取c∈。将（mi，Ui，c）添加到L2中。

6）输出：假设签名伪造成功，敌手A1输出有效签名σ=（U1，…，Un，V）。但是A1没有询问在ID1下对消息m1的签名。伪造成功的条件为y1=0，yi=1（2≤i≤n），B在此过程中没有中止。由y1=0可知，H1（IDi，Pi）=zi（bP），而由yi=1可知，H1（IDi，Pi）=ziP。那么对于i≥2，可以算得Vi=S*i+ri（tP）+cizi（aP），即有e（Vi，P）=e（Yizi+tUi+zici，Ppub）=e（di，Yi）e（Q，Ui）e（hidi，Ppub），其中，hi=H2（mi，Ui），di=H1（IDi，Pi）。

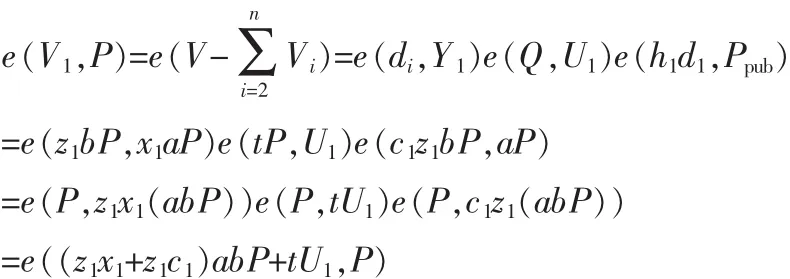
那么算法B可以计算abP出的值：

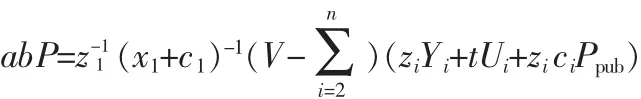
为了完成验证，将给出算法B解决CDH问题的概率是ε*≥ε/（qE+n）e，首先分析B成功的3个事件：

E1：B没有因为A1的局部私钥询问失败而中止。

E2：A1生成一个有效的聚合签名。

E3：E2发生的时候，同时有y1=0和yi=1（2≤i≤n）。

当上面3个事件都发生时，B才能够成功，它的概率可以表示为Pr[E1∧E2∧E3]，将其分解为Pr[E1∧E2∧E3]=Pr[E1]Pr[E1

推论1：B没有因为A1的局部私钥询问失败而中止的概率至少为Pr[E1]≥（1-δ）qE。

证明：由于Pr[y=0]=δ，那么Pr[y=1]=1-δ，因为敌手A1至多进行qE次询问，所以事件E1的概率为Pr[E1]≥（1-δ）qE。

推论2：算法B没有因为A1的局部私钥询问失败而中止，A1的攻击与B的运行相关，与真实的攻击一致，因此有

推论3：算法B没有因为A1输出一个有效签名而失败中

证明：上面的情况产生必须有事件E2发生，且y1=0和yi=1（2≤i≤n），那么其概率值为δ（1-δ）（n-1）。

所以可以计算出ε*=Pr[E1∧E2∧E3]≥（1-δ）qE εδ（1-δ）（n-1）=εδ（1-δ）（n-1）。当δ=1/（qE+n）时，εδ（1-δ）（qE+n-1）达到最大值，即有ε*≥ε/（qE+n）e。

在构造CDH问题中，算法B运行的时间与A1进行询问的时间以及将伪造签名转化成CDH问题的时间t有关。那么存在一个多元一次函数φ，使总的运行时间至多为φ（qH1、qH2，qE，qs，qp）tG1+t。

对于敌手A2的攻击，构造过程与敌手A1类似，就省略了。

由上面的证明可知，算法B可以在敌手A的帮助下解决CDH问题，而CDH问题被认为是难解的，所以方案在随机预言模型下是安全的，具有不可伪造性。

4 结论

本文应用椭圆曲线上双线性对的技术，提出了一个自认证的聚合签名方案。该方案参考了已有的聚合签名的方案，重新构造了一个新的方案，然后将自认证的过程引入到该方案中，这样就能有效地解决密钥托管和安全信道问题，同时保持聚合签名的特性。最后利用计算Diffie-Hellman问题的困难性，证明了该方案在随机预言模型下是安全的。

[1]SHAMIRA.Identity-basedcryptosystemsandsignatureschemes[C]//Proceedings of Crypto’84.Germany:G.Blakley and David Chaum，eds.volume 196 of LNCS.1981:47-53.

[2]GIRAULT M.Self-certified public keys[C]//Proceedings of Eurocrypt’91.USA:Springer-Verlag Berlin，Heidelberg，1991:491-497.

[3]PETERSEN H，HOSTER P.Self-certified keys-concept and application[C]//Proceedings of the Communication and Multimedia Security’97.USA:Chapman，Hall，1997:102-116.

[4]SHAO Zu-hua.Cryptographic systems using self-certified public key based on discrete logarithms[C]//IEE.[S.L.]:Comput.Digit.Teach，2001，148（6）：233-237.

[5]LEE B，KIM K.Self-certified signature[C]//Progress in Cryptology-Indocrypt’2002.LNCS 2551.Germany:Springer-Verlag Berlin，2002:199-214.

[6]SHAO Zu-hua.Self-certified signature scheme from pairing[J].The Journal of Systems and Software，2007（80）:388-395.

[7]BONEH D，GENTRY C.Aggregate and verifiably encrypted signature from bilinear maps[C]//Advance in Cryptography-EUROCRYPT 2003.LNCS 2656.Germany:[S.N.]，2003:416-432.

[8]Cheon J H，Kim Y，Yood H J.A new ID-based signature with batch verification[EB/OL].[2011-02-16].Cryptology ePrint Archive，Report 2004/13.http://eprint.iacr.org/2004/131.pdf.

[9]GONGZheng，LONGYu，HONGXuan，etal.Twocertificateless aggregate signature from bilinear maps[C]//IEEE.Qingdao China:[S.N.]，2007:188-193.

[10]孙华，郑雪峰，于义科，等.一种安全有效的基于身份的聚合签名方案[J].计算机科学，2010，37（5）:62-65.SUN Hua，ZHENG Xue-feng，YU Yi-ke，et al.Secure and efficient identity-based aggregate signature scheme[J].Computer Science，2010，37（5）:62-65.

[11]BONEH D，LYNN B，SHACHAM H.Short signature from the Weil pairing[C]//Advance in Cryptology-Asiacrypt’01.Germany:Springer-Verlag Berlin，2001:514-532.