基于遗传神经网络自适应噪声抵消技术的研究

马莉，韩应征

（太原理工大学信息工程学院，山西太原030024）

信号传输过程中，往往受到噪声或干扰的影响。如何有效地从受到污染的信号中提取有用信号成为急需解决的问题。受污染的信号经由可抑制噪声且时域信号相对不变的滤波器而产生输出，此为最优滤波器。可实现最优滤波的滤波器是维纳滤波器和卡尔曼滤波器[1]，它们都要求已知信号和噪声的先验知识，但在实际中往往无法预先得知。为了使滤波性能提高，滤波器的权系数可随输入信号的变化而发生改变，这称之为自适应滤波[2]。自适应噪声抵消技术是通过与噪声相关的信号来修正滤波器参数，以此实现对噪声的抑制。实际上，它是自适应滤波器的一种变形，它能很好地减除背景噪声的影响以及外界声源干扰，获得高信噪比的信号。常用的自适应滤波器一般有线性和非线性两种[4]。通常环境下的各种噪声间都是非线性且相关的，这种情况下使用线性自适应滤波器则达不到要求。为了有效地消除噪声干扰，往往采用非线性自适应滤波器。但由于其处理非常繁杂，收敛速度缓慢，因此不适合在实际中应用。

神经网络可以模仿并能延伸人脑智能、思维、意识，它具有全新的信息表达方式、高度平行分布处理、联想、自学习和自组织能力，这就为非线性自适应滤波提供了一种新的思路和方法[3-4]。文中将前馈神经网络和遗传算法相结合用于研究自适应噪声抵消。BP算法是前馈神经网络的典型算法，但存在收敛慢、易陷入局部极小点等缺陷问题，而遗传算法是一种随机优化算法，可寻找得到全局最优解。采用遗传算法优化神经网络权值的方式，将两种算法相结合，从而优势互补，扬长避短。此方法缩短了网络学习和计算时间，同时还提高了信噪比。

1 自适应噪声抵消原理

自适应噪声抵消（ANC）系统的处理对象为干扰噪声，它的作用就是抑制掉干扰噪声或者对噪声进行大幅度衰减，从而提高信号传递和接收时的信噪比（SNR）。其原理概述为，首先通过参考通道的输入由自适应滤波器接收；然后在滤波器中，经由一种受误差信号控制的算法自动地调节滤波器的冲激响应，使得输出在遵照最小均方准则的基础上，最接近主通道的干扰信号；最后经求和器使两个通道的信号相减，抵消掉主通道干扰信号。若使用的算法得当，滤波器可在变化的条件下工作，通过不断地自动调整，使误差信号始终保持最小[1]。

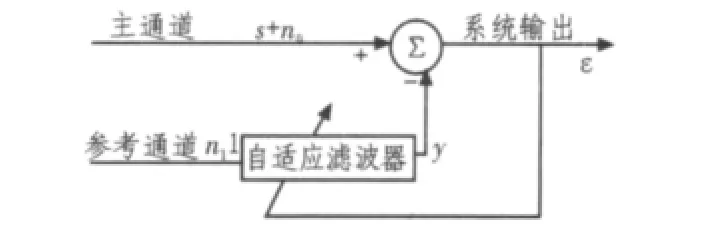
图1 自适应噪声抵消原理框图Fig.1Diagram of adaptive noise cancellation principle

图1为自适应噪声抵消原理框图。如图所示，主通道输入信号为一个背景加性噪声n0加上一个有用的信号s，而参考通道的输入信号n1是与背景加性噪声n0相关的信号，其与有用信号s则无关。假设s、n0与n1都为零均值的平稳随机过程，并且s与n0、n1之间不相关。由图1可知，自适应滤波器的输出y是参考通道输入信号n1的滤波信号，那么整个自适应抵消系统的输出ε为：

将其两边平方，得：

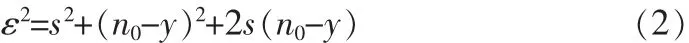
对上式两边分别取数学期望，得：

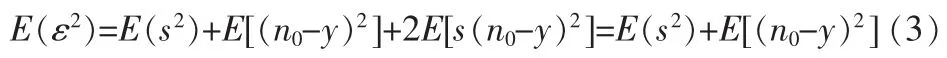
由于信号功率E（s2）与自适应滤波器的调节并无关联，因此，通过滤波器的调节可使得E（ε2）最小，也意味着E[（n0-y）2]是最小，那么E[（ε-s）2]同样最小。由此可得：自适应噪声抵消系统的输出信号ε与有用信号s的均方差达到最小值。只要参考通道的输入与被抵消的噪声信号间相关，那么当有用信号从参考通道输入后，则有必定有一部分将会被抵消。在理想状态下，当y=n0，则ε=s。

然而实际应用中，滤波器在ε的控制下，根据最小均方准则不断反复修正自适应滤波器的权值，才使整个系统输出信号均方值E（ε2）保持最小，从而达到有效抵消噪声的目的。

2 遗传神经网络

神经网络和遗传算法都属于仿生学范畴，二者结合可优势互补，用于解决复杂的非线性优化问题。

神经网络是个高度复杂的非线性网络系统，由大量神经元节点互相连接构成，应用仿真处理方法，建立粗略近似的数学模型，从而反映出人脑的基本特性。根据神经元所起作用不同，可划分为输入层神经元，输出层神经元和隐层神经元。神经元之间的连接由加权系数决定，其作用为传递前一层神经元对下一层的影响。神经网络学习过程，是通过加权系数的变化来实现的。神经网络互连方式不仅决定了网络的能力，同时反映了神经网络的结构。神经网络按结构划分为前馈网络、反馈网络、随机网络和自组织网络等。其中，以前馈神经网络的应用最为广泛。它的网络结构是单向多层的，所有神经元分层排列，只与前一层的神经元连接，同层间无连接、无反馈，信息传送沿一个方向进行[3]。

神经网络模型的建立关键在于权值矩阵，它的选择借助于网络训练来实现。用来训练网络的算法称之为学习算法，而误差反向传播（BP）算法是典型的前馈网络学习算法，易于局部搜索。通常沿梯度下降方向的搜索算法对初始权向量都异常敏感，且计算中存在着收敛速度慢，易陷入局部极小点的问题[2]。利用BP算法进行学习的网络称为BP神经网络。

遗传算法是一种借鉴生物界自然选择和遗传进化机制的随机化搜索算法，具有“生成+检验”的特征，适用于函数优化问题。遗传算法的实现包括5个基本要素：1）参数编码；2）初始种群的生成；3）适应度函数的设计；4）遗传操作设计；5）控制参数设定（这主要是指群体规模大小和使用遗传操作的概率），这5个要素共同构成遗传算法的核心内容。该算法在运行过程中以概率选择为主要手段，同时对问题空间的多个解进行处理，具有较强的鲁棒性，适于全局搜索，故避免了陷入局部最小[5]。可利用GA的这些优势去克服BP算法存在的缺陷，将其用于优化BP神经网络，简称为遗传神经网络。

GA和BP的结合点不同，则优化方式也不同。文中采用GA反复优化神经网络权重，直到生成的子代种群的平均值不再有效增加，即进入进化停止状态[6]。经遗传算法优化后得到的参数组合接近于最佳组合，在此基础上用BP算法进行精调，就可以快速获得最优解。

BP-GA混合算法的步骤如下：1）分析问题，给定目标函数、设计变量及约束条件；2）设定恰当的训练样本集，进行计算；3）训练神经网络；4）应用遗传算法进行寻优；5）用训练好的神经网络来检验优化结果。若满足要求，停止计算；反之，重新将检验解放入训练样本集，重复执行3～5直到达到要求。

3 遗传神经网络自适应噪声抵消仿真

依据自适应噪声抵消系统原理，结合神经网络和遗传算法二者特点，共同构成遗传神经网络自适应噪声抵消系统，如下图2所示。

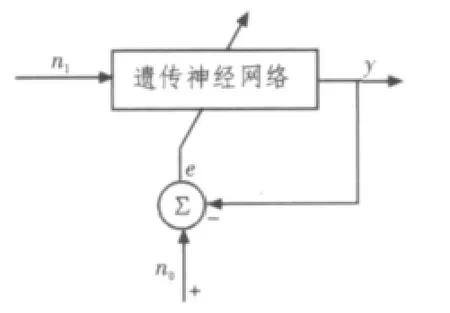
图2 遗传神经网络辨识自适应滤波器框图Fig.2Diagram of genetic neural network identificative adaptive fiter

大量实验证明，含有隐层的神经网络可实现任意域的分割。文中设定一个三层BP网络对自适应噪声抵消器进行仿真。神经网络结构如图3所示，网络中输入层、隐层和输出层节点数分别为1、4、1[7-8]。设定网络隐层函数为tansig函数，则神经元的输入范围（-∞，+∞）映射到（-1，+1）。若网络输出层是Sigmiod型神经元，则网络输出就被限制于很小的范围；若为purelin型线性神经元，则网络的输出为任意值。

遗传神经网络自适应抵消系统利用MATLAB仿真时，设定输入为余弦信号，由遗传神经网络和加法器组合构成自适应噪声抵消系统，输入信号经由自适应噪声抵消系统作用后产生输出。其中，采用了遗传算法优化神经网络权重的方法。

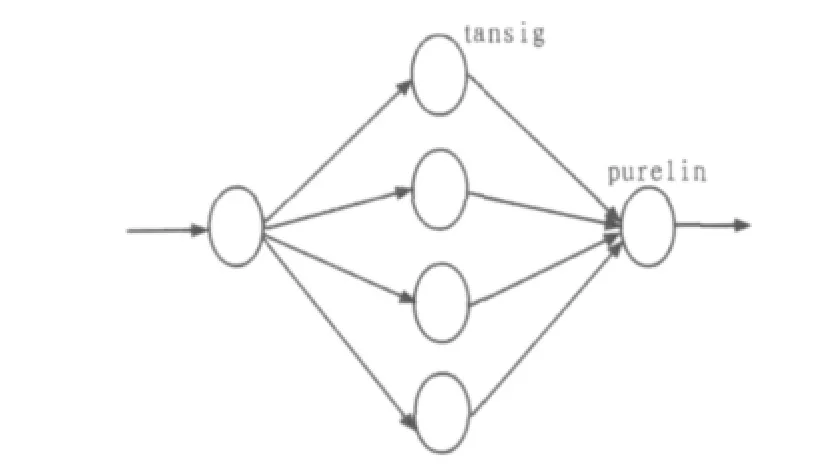
图3 BP神经网络结构图Fig.3Structure diagram of BP neural network

仿真实验中，先用初始样本进行网络训练，经过3 000次训练后的误差小于0.01，因此满足系统要求。然后进行仿真输出，仿真结果如图4所示。图4中的a~d图分别为原始信号，相关噪声信号，叠加噪声的余弦信号及抵消噪声后的原始输入信号。

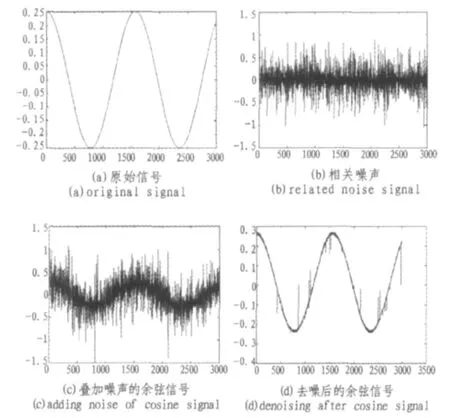
图4 仿真效果图Fig.4Figure of simulation results

仿真实验说明，经GA优化权值后的网络具有良好的拟合性，主通道信号经过求和器与遗传神经网络输出抵消后，得到基于最小均方准则下对输入信号的最佳拟合。

综上所述，基于遗传算法优化神经网络权值的自适应噪声抵消系统达到了理想的效果，有效的减除了噪声使信号保持了原来的特性，因此，对遗传神经网络自适应噪声抵消的研究是非常有意义的。

4 结论

自适应噪声抵消技术的目的是减除噪声而并不是滤除噪声，因此性能上更优于传统滤波器。文中提出的由GA-BP混合神经网络构成的非线性自适应噪声抵消系统能快速有效地减除噪声。其结合了BP算法和遗传算法各自的优点，所生成的遗传神经网络在自适应抵消技术领域中，性能更优于传统的ANC。

在GA-BP混合神经网络构成的非线性自适应噪声抵消系统中，输入待测信号，进行模拟仿真实验，得出GA与BP相混合的神经网络系统无论是运行速度还是运算精度都有着显著提高，去噪效果更优异，同时在某种程度上提高了信噪比。本文所提出的BP网络和GA算法结合产生的混合神经网络，其理论思想与仿真结果基本保持一致。

[1]Widrow B，Stearns S D.Adaptive signal processing[M].US:Prenice-Hall，Inc.1985.

[2]贺宽，黄涛.基于Matlab的自适应滤波器设计[J].武汉理工大学学报，2008，30（1）：70-73.HE Kuan，HUANG Tao.Adaptive filter design based on Matlab[J].Journal of Wuhan University of Technology，2008，30（1）:70-73.

[3]飞思科技产品研发中心.神经网络理论与MATLAB 7实现[M].北京：电子工业出版，2005.

[4]张贤达.现代信号处理[M].2版.北京：清华大学出版社，2002.

[5]Nara K.Implementation of genetic algorithms for distribution system loss minimum reconfiguration[J].IEEE Trans on Power Systems，1992，7（3）:1044-1049.

[6]陈颖琪.进化计算与神经网络的结合[J].红外与激光工程，

1999，28（4 ）：6-9.CHEN Ying-qi.Combination of evolutionary computation and artificial neural network[J].Infrared and Laser Engineering，1999，28（4）：6-9.

[7]董春利.基于神经网络的自适应非线性滤波的研究[D].兰州：兰州大学，2004.

[8]张艳红.基于神经网络的自适应滤波器的研究与实现[D].天津：南开大学，2004.