Alpha稳定分布随机变量仿真及模型参数估计

康亚明，曹保卫

（1.榆林学院信息工程学院，陕西榆林719000；2.榆林学院图书馆，陕西榆林719000）

α稳定分布是满足广义中心极限定理的唯一一类分布。常规高斯分布的动因也是中心极限定理，可见α稳定分布在理论上的合理性与高斯分布是一样的。α稳定分布能够描述更加广泛的数据，甚至可以描述很多不满足中心极限定理的数据，因此具有更普遍的意义。α稳定分布能够非常好的和数据相吻合。Stuck等人已经证明，电话线路中的噪声可以有效地利用α稳定分布描述[1]。Nikias等人证明了α稳定分布是描述大气噪声的非常好的模型[2]。Ilow的研究表明稳定分布与无线网络中的多径干扰和雷达系统的反向散射回波相符合[3]。Mandelbrot利用α稳定分布对经济时间序列建模工作也很成功[4]。

1 Alpha稳定分布序列分布

1.1 Alpha稳定分布的概念

α稳定分布是一类适用范围很宽并得到广泛应用的随机信号模型，包括高斯分布（α=2）和分数低阶α稳定分布（0＜α＜2）两种情况。与大多数的统计模型不同，除了几种已知的分布情况之外，α稳定分布没有一个概率密度函数的闭式解。1978年Sutkc利用特征函数对α稳定分布作了最有效的描述[5]，α稳定分布的特征函数可以表示为：

其中

可见，通过4个参数:α，a，β，γ便可以完全确定一个稳定分布的特征函数。其中

1）α称为特征指数，它是被唯一确定的。特征指数用来度量分布函数拖尾的厚度。一个稳定分布的随机变量，其值越小，表明其拖尾越厚，则偏离其中心值（均值或中值）的样本越多。其α值越大，则越趋向于高斯过程。α=2表示分布为高斯分布。α=l，β=0表示分布为柯西分布。

2）γ称为分散系数，其意义与高斯分布中的方差类似，在高斯分布的情况下等于方差的一半。

3）β称为对称参数，β=0表示分布为对称α稳定分布或称SαS。

4）a称为位置参数0，对于SαS分布，当1＜a≤2时，a为α稳定分布的均值。当0＜a＜1时，a表示其中值。

分数低阶α稳定分布的显著特征是它具有比高斯分布的指数（exponential）拖尾明显厚的代数（algebraic）拖尾，α越小，拖尾越重。这个性质使得分数低阶α稳定分布可以较为理想地描述某些冲激信号。

图1给出了不同的特征指数α下的标准SαS分布的概率密度函数曲线。从图中可以看出，α=2时的SαS概率密度函数曲线与零均值方差为2的高斯分布一致，α=1时与柯西分布一致。同时，SαS分布的概率密度函数保留了许多高斯分布的特征：光滑，单峰分布，关于中值或均值对称的，钟型。对比标准正态分布概率密度函数和SαS密度函数的细节可以看到，非高斯α稳定分布与高斯分布有以下不同:x的绝对值较小时，SαS密度函数比正态分布有更尖的峰，对于一些中间值，SαS分布低于正态分布。最重要的是，SαS分布的概率密度函数有着比高斯分布更厚重的拖尾，α的值越小，拖尾越厚重。

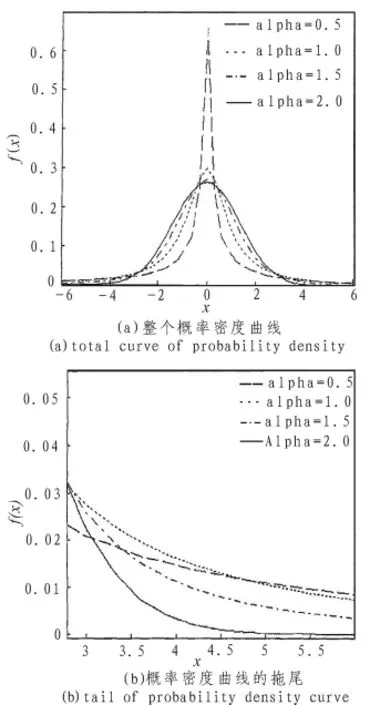
图1 特征指数α取不同值时的SαS分布概率密度函数曲线Fig.1Probability density function curve of SαS distribution for different α

1.2 Alpha稳定分布的两个重要特性

α稳定分布的两个重要特性是稳定特性和符合广义中心极限定理特性，Breiman于1968年提出α稳定分布的稳定特性和广义中心极限定理特性[2]：

1）稳定特性一个随机变量X具有稳定分布的充分必要条件为，存在随机变量X1andX2相互独立，且具有与X相同的参数，对任意常数α1，α2有常数a和b使等式α1X1+α2X=aX+b成立。Xd=Y表示随机变量X和Y具有相同的分布。利用稳定分布的特征函数，可以得到更具一般性的结论：如果随机变量X1，X2....，Xn是统计独立的，且均为符合相同的（α，β）参数确定的稳定分布，则具有形如∑ajXj的所有线性组合都是稳定分布的，且具有相同的参数α和β。

2）广义中心极限定理特性X1，X2，....，Xn为独立同分布的随机变量，当n→∞时，它们的极限和Sn=（X1，X2，....，Xn）/αn-bn的分布为稳定分布。特别地，如果Xi（i=1，2，...，n）是独立同分布的且具有有限方差，那么此极限和的分布为高斯分布。即一般的中心极限定理。

因此，用α稳定分布作为基本的统计建模工具的理论依据如同高斯分布的情况相同，均源于中心极限定理。中心极限定理是指，具有有限方差的充分多的独立同分布（IID）的随机变量，它们和的分布近似为高斯分布。广义中心极限定理指出，无限多的独立同分布随机分量，无论是否有有限的方差，它们的和将收敛于稳定分布。因此，非高斯稳定分布源于随机变量的和，这和高斯分布是一样的。如果观测信号或噪声可被看作很多独立同分布分量叠加的结果，则由广义的中心极限定理可知，用稳定分布模型建模是合适的。

2 α随机变量的产生

在进行计算机仿真研究中，经常需要利用特定的算法，根据给定的要求来产生有关信号和噪声。假定我们要产生阶数为（0＜α≤2）的α稳定分布序列x（n）,满足α=0和－1＜β＜1。若α=1，则定义

若α≠1，则定义

这样满足给定α值的分数低阶α稳定分布的随机变量X由下式给出

对上述过程进行循环，则可以得到一个满足给定条件的分数低阶α稳定分布序列x（n）。

3 数据产生结果

1）不同α值对峰值的影响对比如图2所示。

2）不同β值对累积概率分布的影响如图3所示。

图2 概率累积分布（β=0）Fig.2Cumulative probability distribution（β=0）

?图3不同β值对累积概率分布的影响Fig.3Effect to the cumulative probability distribution of differentβ

3）不同α值对累积概率分布曲线的拖尾的影响，如图4所示。

图4 概率密度曲线Fig.4Probability density curve

4 动态样本方差检测

上面的内容简单介绍了α稳定分布的基本模型及性质，在实际的应用问题中，往往需要判断给定序列是高斯分布（α=2）的，还是分数低阶α稳定分布（α＜2）的，以便决定采取不同的信号处理方法。判断序列高斯特性的常用方法是计算该序列的动态样本方差[6]。若xk，k=1，2，...，N是一个随机序列，对于1≤n≤N，其动态样本方差定义为

其中

绘出S2n随n变化的曲线，如果序列为高斯分布，则其具有有限的方差，对应的S2n曲线收敛为一个有限值。反之，若序列为非高斯的α稳定分布序列，则它没有有限的方差，对应的S2n曲线不能稳定的收敛。由此可以粗略判断给定序列是否为高斯分布的序列。这种方法称为动态样本方差检验。

图5 α=1.5，β=0时的动态样本方差Fig.5Dynamic sample variance of α=1.5，β=0

图6 α=2.0，β=0时的动态样本方差Fig.6Dynamic sample variance of α=2.0，β=0

由图5与图6对比可知，当α≠2.0时，方差不能趋向于一个恒定值，当α=2.0时α稳定分布的方差值趋向于一个均值，因为当α=2.0时α稳定分布就是一个正态分布。

5 α稳定分布参数估计

如果知道一个分布序列如何得知它们的具体参数，从而方便一个系统的仿真更能很好地描述实际情况，下面具体介绍如何得出一个已知序列的α，β的近似值。

由于对于不同β值的α分布，只要α给定，无论β值如何变化，它的累积概率分布函数的峰值不会变化；与此相同，如果β值一定，无论α如何变化，它的累积概率分布函数的偏度不会变化。基于上数特性，可以建立一个数据库，从得知的已知分布序列的累积概率分布的峰值和偏度可以大致得知该分布近似于的α，β两个参数。

通过已知标准的α稳定分布序列得知以下参数：

表1 偏度和峰值分布对照表Tab.1Compared table of skewness and peak

例如：已知一个分布序列的累积概率分布函数的参数为：偏度：－0.705 6峰值：109.100 5，查表1可知该分布的大致范围为0.4＜β＜0.6，0.6＜α＜0.8，而事实上这是一个α=0.7，β=0.51的α稳定分布。

6 结束语

本文通过描述α分布的累积概率密度函数的图像来分析α稳定分布的特性，结论基本符合要求。通过对α稳定方差的描述可以得出α稳定分布和正态分布的差异，得出正态分布是α稳定分布的一个特殊情况，所以α稳定分布更能描述信道中的噪音。最后做了未知序列的参数估计，本估计比较粗略，可以更近一步细化估计，但是考虑到工程要求，只做误差为0.2的参数估计。

[1]Stuek W，Kleiner B.A statistieal analysis of telephone noise[J].Bell Syst Tech J，1974，53（7）:1263－1320.

[2]Nikias CL，Shao M.Signal proeessing with alpha-stable distributions and applieations[M].New York:Wiley，1995.

[3]Engin K E.Signal proeessing with fraetional lower order environments:aleast lp-norm approaeh（PHD thesis）[M].Signal Proeessing and Communieations Laboratory，Department of Engineering，University of Cambridge，1998.

[4]Mandelbort B.The variation of certain speeulative priees[J].Bussiness，1963（36）:394－419.

[5]邱天爽，张旭秀.统计信号处理－非高斯信号处理及应用[M].北京：电子工业出版社，2004.

[6]杨伟超，赵春晖,成宝芝.Alpha稳定分布噪声下的通信信号识别[J].应用科学学报，2010，28（2）：111－114.YANG Wei-chao,ZHAO Chun-hui,CHENG Bao-zhi.Recognition of communicationsignalsinnoisewithalphastable distribution[J].Journal of Applied Sciences,2010，28（2）：111－114.