基于有限元分析的装载机铲斗结构优化

钟丽萍

(沈阳职业技术学院,辽宁 沈阳 110045)

铲斗是装载机的重要组成部分,主要实现装载机的铲掘和装卸物料作业.传统的设计状况不能满足结构优化及应力分析的需要,因此需要专业的CAE软件来进行结构优化.Pro/E是美国参数技术公司(PTC)开发的多项技术集成软件,其功能强大、用途广泛,是新一代CAD/CAM集成开发环境.ANSYS是由美国ANSYS公司推出的大型有限元分析软件,但实体建模功能有限,大多数情况下需要从CAD软件导入.因此,本文利用Pro/E和ANSYS各自的优势,在Pro/E中完成铲斗的实体建模,然后将其导入ANSYS中进行有限元分析及结构优化,从而解决实际工程问题.

1 实体建模

本文以某公司生产的ZL50装载机铲斗为研究对象,采用Pro/E对其进行实体建模.由于是在装载机铲斗几何模型的基础上建立有限元模型[1],而且根据经典薄壳理论假设,厚度小于中曲面轮廓尺寸1/5的为薄板,所以它是典型的板壳问题.

铲斗的实体模型如图1所示.通过中曲面建立的几何模型,既可以使铲斗的几何模建立得到简化,又提高了工作效率.

2 工程分析

将Pro/E铲斗实体模型无缝导入ANSYS软件[2].在Pro/E中建立实体模型时存在重叠或多余的线,首先通过布尔操作使得模型的面与面结合在一起,然后划分网格并进行相关的有限元分析.

2.1 铲斗的工况选取

由于铲斗工作时的物料种类和作业条件等工况的不同,它的受力情况也不同,但以铲入、掘起正载工况,以及铲入、掘起偏载工况最为恶劣,因此取正载和偏载2种工况为计算工况,如图2所示.图中,Rx、Ry分别为铲斗受到的水平和垂直力.

2.2 有限元模型的建立

板壳问题可采用空间板壳单元进行网格划分[3].本文选取SHELL63单元,SHELL63单元适用于同时受横向载荷和膜载荷的薄板结构,适用于应力硬化和大变形分析问题.该单元在每一个节点有6个自由度:沿坐标轴x,y,z方向的线位移及绕坐标轴x,y,z的角位移.对模型进行划分网格,共划分为8489个单元.划分网格后的铲斗模型,如图3所示.

图1 铲斗实体模型Fig.1 Solid model of loader bucket

图2 正载工况和偏载工况Fig.2 Working conditions of normal loading and bias loading

图3 划分网格后的铲斗模型Fig.3 Bucket model after meshing

2.3 约束条件的确定

铲入、掘起偏载工况时,约束部位为动臂铰孔、动臂铰孔下沿(左孔)及上沿(右孔)120°范围内节点的纵向(x)及竖向(y)自由度限制为零.铲入、掘起正载工况时,约束部位同偏载工况,但动臂左、右铰孔均限制上沿120°范围内各节点.

2.4 载荷的计算与施加

取额定装载量50 kN,根据以上假设,可计算出铲斗所受水平力Rx和垂直力Ry.Pkpmax为装载机的最大牵引力,则水平力的大小为Rx=Pkpmax=140 kN;垂直力大小受装载机的纵向稳定条件的限制,其大小为Ry=145 kN.

图4 销孔接触区节点力的等效处理Fig.4 Equivalent processing of node stresses in pinhole contact field

在对装载机进行整体计算时,总是假设铰点力是以集中力的形式作用的,单独对铰销分析时,铰销和销孔之间接触应力的分布与材质、接触方式、配合公差等诸多因素有关.根据经典弹性理论关于接触问题的研究,销孔接触应力的分布为

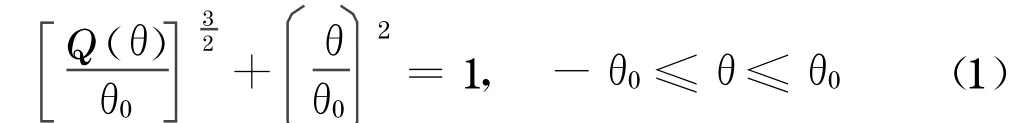
如图4所示,把与拉杆铰接的孔沿圆周上剖分为24个节点,沿圆周上剖分24个节点情况下处于接触区的各节点等效力的计算式,可根据静力系和力的等效原理,列出y方向的等效力方程:

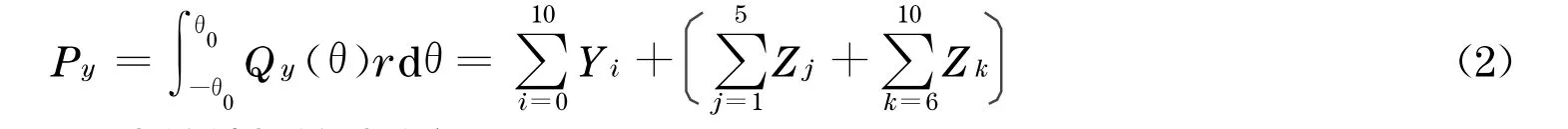
式中:Py为铰点径向力;Qy(θ)为铰销与铰孔之间的作用力分布函数;r为铰销半径;Yi为y向i节点处的分力;Zj,Zk分别为z向j,k节点处的分力,Zj=-Zk(j=1,2,3,4,5;k=6,7,8,9,10),i,j,k为相应的节点编号.从式(2)推导得圆周上剖分24个节点情况下处于接触区的各节点等效力的计算式,如表1所示.

2.5 有限元求解与结果分析

对铲入、掘起正载工况和偏载工况进行有限元求解计算,分别得到铲斗的米赛斯等效应力云图[4],如图5,6所示.

正载工况下,在铲斗斗底及主刀板与侧立板的接合处等效应力较大,最大应力出现在铲斗边耳板下部与铲斗斗壁的结合处,最大等效应力为190.540 MPa.偏载时最大等效应力为226.650 MPa.16 Mn的屈服极限为σs=345 MPa,许用极限为[σ]=230 MPa(取安全系数n=1.5),故铲斗的强度满足.由等效应力云图可知,铲斗的某些部位应力太小,设计过于保守,设计不尽合理,因此在保证铲斗功能及满足强度的条件下,为了节约材料,有必要对铲斗进行结构优化.以铲斗的质量为目标函数,对铲斗的各板板厚进行结构优化,使得铲斗各处应力均匀分布,从而达到近似等强度设计,得到满足强度要求的最佳方案[5].

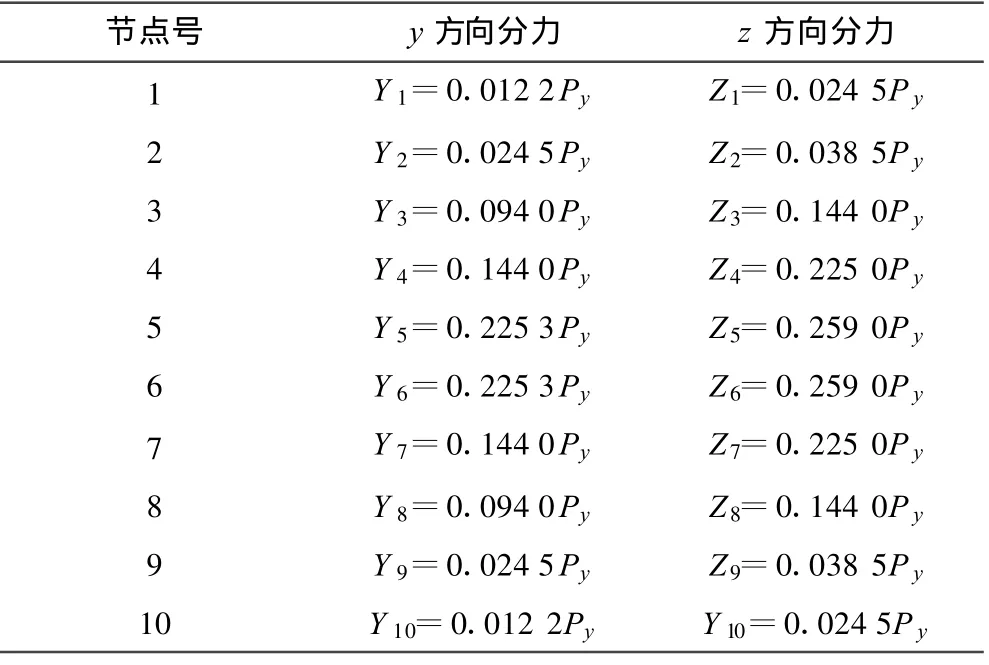
表1 接触区的各节点等效力的计算式Tab.1 Equivalent force calculation method of all nodes in contact field

图5 铲斗在正载工况下的等效应力图Fig.5 Equivalent stress of bucket under normal loading

图6 铲斗偏载工况下的等效应力图Fig.6 Equivalent stress of bucket under bias loading

3 铲斗模型结构优化

结合ANSYS提供的优化设计功能,在强度分析的基础上进行铲斗结构参数的优化.

3.1 铲斗结构优化设计数学模型

该优化模型以铲斗的总质量为目标函数,则优化设计的数学模型可表示为

式中:ti为第i个构件的板厚;n为铲斗不同板厚构件的总数;timin和timax为第i个板构件板厚的上下限值.

式中:W(x)为铲斗的总质量;ρ为材料密度;Ai(i=1,2,…,n)为板面积;C为强度约束,σs为材料的屈服强度.

3.2 优化变量的选择

优化变量包括设计变量、状态变量和目标函数.以斗壁、侧板、耳板和加强板等零件的厚度尺寸为设计变量,即x={t1,t2,t3,t4,t5,t6,t7}.各物理量所代表的具体含义见表2.状态变量是约束设计的数值,它是设计变量的函数,它们的函数关系通常不是显式的.在结构优化中的状态变量为强度状态变量.目标函数是要尽量减小的数值,它也是设计变量的函数,本文以铲斗的质量为目标函数.

3.3 优化方法

ANSYS结构优化中有2种优化方法:零阶方法和一阶方法[6].零阶方法是最常用的方法,使用所有因变量(状态变量和目标函数)的逼近,可以有效地处理绝大多数的工程问题.一阶方法采用因变量的一阶偏导数,通过对目标函数逼近加罚函数的方法将问题转换为无约束的问题,在每次迭代中,计算梯度(用最大梯度法或共轭方向法)确定搜索方向,从而求得最小值.与零阶方法相比,优化精度更高,所以本文采用一阶方法.

4 优化结果与分析

表2 尺寸优化结果Tab.2 Size optimization result

由于ANSYS优化结果中各板厚并不正好是钢板厚度系列值,所以应该考虑到加工工艺要求,并作相应修改,优化结果见表2.

由表2可以看出:优化结果方案使铲斗的重量减轻了48.429 kg(4%),达到了满足强度要求的同时减轻质量的目的;铲斗整体应力水平有所提高,提高了材料的利用率;铲斗的最大等效应力227.4 MPa,仍然小于16Mn的许用应力230 MPa,优化是合理的[7].

2种工况下,各板板厚、最大等效应力及铲斗质量与迭代次数之间的关系如图7～11所示.

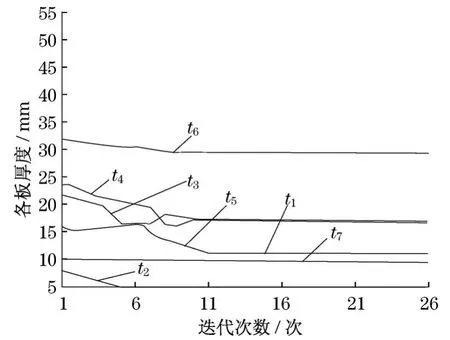
图7 正载优化时各板板厚与迭代次数关系Fig.7 Relations about slab thickness and number of iterations when normal load optimization

图8 正载优化时最大等效应力与迭代次数关系Fig.8 Relations about maximum equivalent stress and number of iterations when normal load optimization

5 结论

通过结构分析与优化可知:利用ANSYS软件进行对铲斗进行了结构分析及结构优化,可使铲斗的质量减少了48.429 kg,减重率4%.得到优化的各项数据和各迭代阶段的详细数据指标,分析结果可靠性高,并可以大大缩短设计周期,能够在保证设计要求的前提下提高产品设计水平.

图9 正载优化时铲斗质量与迭代次数关系Fig.9 Relations about bucket quality and number of iterations when normal load optimization

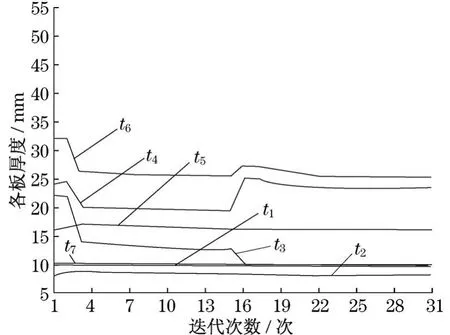
图10 偏载优化时各板板厚与迭代次数关系Fig.10 Relations about slab thickness and number of iterations when bias load optimization

图11 偏载优化时最大等效应力与迭代次数关系Fig.11 Relations about maximum equivalent stress and number of iterations when bias load optimization

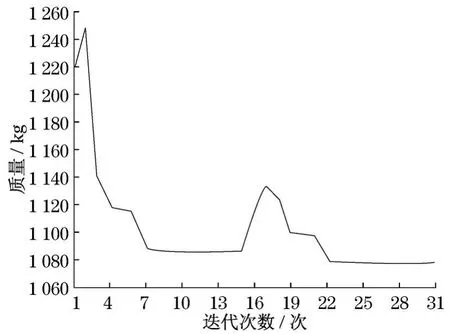
图12 偏载工况优化时铲斗质量与迭代次数关系Fig.12 Relations about bucket quality and number of iterations when bias load optimization

[1]崔小松,曾志新,孟令冬.基于Pro/Engineer的装载机工作装置的运动仿真和有限元分析[J].机电工程技术,2005,34(3):70-72.CUI Xiaosong,ZENG Zhixin,MENG Lingdong.Motion emulation and FEA of operating device of loader based on Pro/Engineer[J].Electromechanical Technology,2005,34(3):70-72.

[2]范文杰,张子达,文广.挖掘装载机工作装置有限元分析[J].土石方机械与施工技术,2006(2):45-47.FAN Wenjie,ZHANG Zida,WEN Guang.Finite element analysis on loading working equipment of backhoe loader[J].Earthwork Machinery and Construction Technology,2006(2):45-47.

[3]石沛林,张子达.装载机工作装置有限元分析及横梁位置确定[J].工程机械,1999(10):20-22.SHI Peilin,ZHANG Zida.Finite element analysis of working equipment and decision of cross beam on loader[J].Engineering Machinery,1999(10):20-22.

[4]李海峰.装载机工作装置有限元分析[J].重型汽车,2003(1)18-19.LI Haifeng.Finite element analy sis of loader equipment[J].Heavy T ruck,2003(1):18-19.

[5]李柳,程志红,陈光柱,等.装载机工作装置参数化建模优化分析[J].煤矿机械,2006,27(9):34-35.LI Liu,CHENG Zhihong,CHEN Guangzhu,et al.Optimum analy sis of working device of loader parametrization building model[J].Mining Machinery,2006,27(9):34-35.

[6]李德军,杨超英,刘长全,等.轮式装载机铲斗的有限元分析[J].山东工业大学学报,1995,25(2):197-200.LI Dejun,YANG Chaoying,LIU Changquan,et al.Finite element analysis of the bucket in the wheeled loader[J].Journal Shandong University of Technology,1995,25(2):197-200.

[7]RUST W,SCHWEIZERHOF K.Finite element limit load analysis of thin-walled structures by A NSYS(implicit),LS-DYNA(explicit)and in combination[J].T hin-Walled Structures,2003,41(2):227-244.