PowerCube模块化机器人工作空间计算

石 磊,许明恒,邓维鑫,刘 波

(1.西南交通大学 机械工程学院,四川 成都 610031;2.西南科技大学 制造科学与工程学院,四川 绵阳 621010)

随着机器人技术的深入发展,现代机器人朝着模块化、智能化、微型化、仿生化方向发展[1,2].其中,模块化机器人可利用一些不同尺寸和性能的可交换的连杆和关节模块组合成特定构型,能够方便组装和拆卸.作为一种新型机器人,模块化机器人已引起众多研究者的兴趣.具有代表性的PowerCube模块化机器人是德国AMTEC公司生产的产品,它将运动控制、PID(Proportion Integration Differentiation,PID)控制及大功率电子设备集成到运动模块,可大大减少重复性的设计工作,具有精度高、噪声低、运行平稳、组装灵活和应用简单等特点,在军事、航天、船舶、环境检测等领域都有广阔的应用前景[3].在模块化机器人设计、运动规划及动力学控制过程中,工作空间是1个需要考虑的重要问题.研究者们在该领域做了大量的工作.赵杰采用降维搜索和二分法计算工作空间边界点,确定机器人工作空间多连域截面封闭曲线,实现了可重构模块化串联机器人工作空间的自动计算[4].蔡蒂根据喷涂机器人工作情况,采用蒙特卡洛法分析其工作空间并通过机器人正向运动学方程求解得到机器人末端点的集合,从而有效地得到6自由度喷涂机器人的可达工作空间[5].工作空间的确定概括起来主要有3种方法:图解法、解析法和数值法.近年来,随着三维建模软件的不断发展,仿真法被用来求解机器人工作空间.仿真法是在对机器人的结构进行建模的基础上,利用仿真的形式跟踪手臂末端轨迹,从而绘制和计算出机器人工作空间[6].虽然工作空间的确定方法不少,但研究者们大多采用单一的工作空间确定方法,无法保证机器人工作空间研究的正确性.

基于上述认识,本文运用D-H坐标系理论为基础建立了PowerCube模块化机器人的运动学模型,并开展了正向运动学分析.在比较现有的机器人工作空间求解方法的基础上,分别利用解析法和数值法绘制和计算出机器人的工作空间.

1 PowerCube模块化机器人运动学分析

PowerCube模块化机器人由各类通用模块和连接附件组装而成.根据工作和环境的需要,选用不同的模块可以得到所需的机器人.文献[7]给出了一种构型的PowerCube模块化机器人,如图1所示.该机器人是由旋转模块、手腕模块和夹持模块等组成的冗余度机器人.当锁定第三个模块时候,构成6自由度机器人.该机器人前3个模块主要用于确定手腕参考点的位置,后3个模块的轴线交于一点即手腕参考点,用于确定手腕的方位.

图1 PowerCube模块化机器人Fig.1 PowerCube modular robot

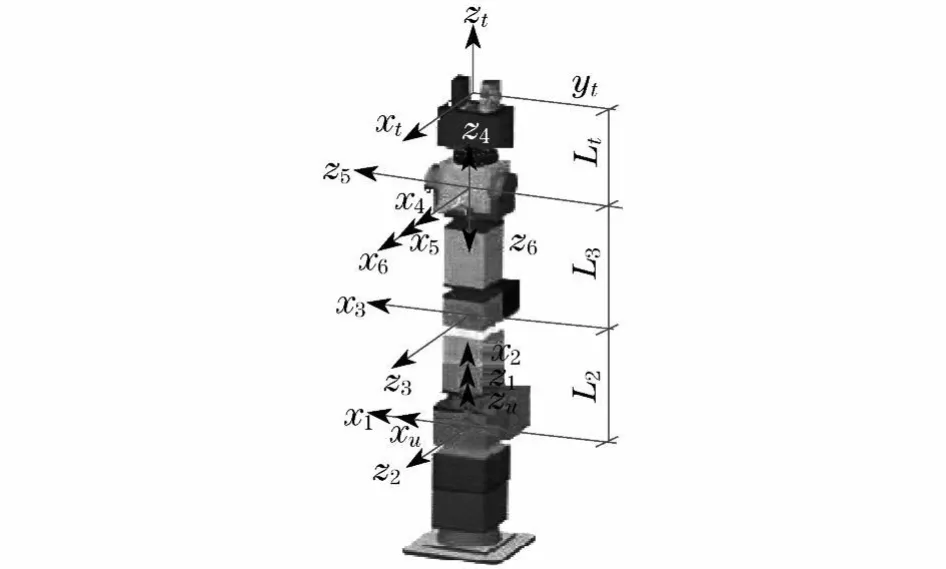
图2 PowerCube模块化机器人各连杆坐标系Fig.2 Coordinate system of link of modular robot

1.1 连杆坐标系和连杆参数

坐标系的设定采用D-H方法,杆件编号从基座至末端执行器依次为0,1,…,6,t.如图2所示建立模块化机器人的连杆坐标系.图中的L2,L3,Lt由实际测量可得到各自大小,分别为L2=287mm,L3=315mm,Lt=226mm.根据所建立的连杆坐标系确定模块化机器人的结构参数和运动参数,如表1所示.

表1 连杆参数Tab.1 Parameter of link

表1 中,ai-1为zi-1与zi的公垂距 ;αi-1为 zi-1与 zi的交错角;di为 xi-1到 zi的交点到Oi的距离 ;θi(i=1,2,…,6)为各模块的关节变量.

1.2 运动学方程

运动学方程表示末端执行器的位姿与各关节变量之间的关系.根据连杆坐标系和连杆参数,可以得到模块化机器人的运动学方程为

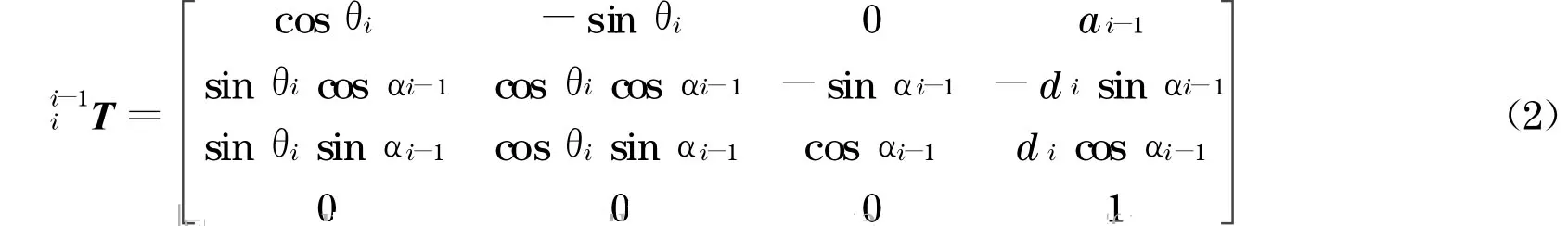
机器人末端坐标系描述机器人末端位姿.它的原点在末端执行器上某点,方向由正交矢量n、方位矢量o和接近矢量a来描述,位置由位置矢量p来描述.将连杆参数代入式(1)和式(2),得到模块化机器人的末端相对于基坐标系的位姿,可表示为

2 工作空间描述

模块化机器人的工作空间是指末端执行器的夹持中心E在空间活动的最大范围,即末端执行器的夹持中心所掠过的空间.设末端坐标系的原点为夹持中心,则夹持中心的位置矢量 p可以由运动学方程和末端坐标系的位姿表达式得到:

式中:xE,yE,zE为夹持中心在基坐标系下的坐标;qi(i=0,1,…,6)为模块化机器人的广义坐标.

用集合的方法,模块化机器人的工作空间W,可表示为

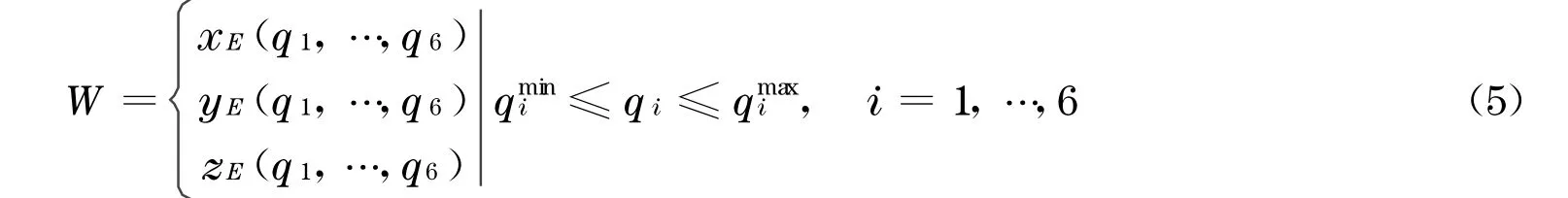
因此,对1个给定构型的机器人,工作空间由广义坐标qi决定.对于转动副,广义坐标qi就是其关节变量θi.

3 工作空间的确定方法

机器人工作空间的确定方法大体上分为图解法、解析法和数值法3种.随着计算机能力的不断增强,图解法已日趋淘汰,研究者们越来越倾向于后2种方法.

3.1 蒙特卡罗数值法

蒙特卡罗方法(又称随机模拟方法)与一般数值计算方法不同,它是以概率统计理论为基础的1种计算方法,经常被用来描述某些随机的物理现象.采用蒙特卡罗数值法进行计算可以得到近似的工作空间.夹持中心的位置矢量与关节变量相关,所有关节变量在取值范围内随机取值,由此所得到的末端点随机值的集合构成了机器人的工作空间.

在MATLAB中利用RAND函数产生随机值作为一个随机步长变量,可以得到1组关节变量值,随机关节变量由式(6)求得:

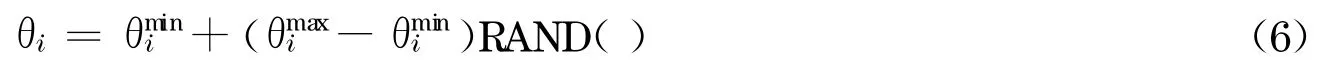
式中:θmini 和θmaxi 分别为第i个关节变量的最小最大值.

将式(6)代入运动学方程,求得相应末端执行器可到达的空间位置点.设定循环次数进行计算,利用关节变量到工作空间的映射关系,产生近似的工作空间的点云数据.按一定的比例以打点的方式显示在图形设备上,可得到模块化机器人的工作空间.当循环次数越多时,计算量越大,近似工作空间与理论工作空间的误差越小.

设定循环次数为10000次,利用蒙特卡罗方法绘制模块化机器人的近似工作空间云图,如图3所示.图4～6分别表示工作空间在xOy、yOz、xOz 3个平面的投影图.

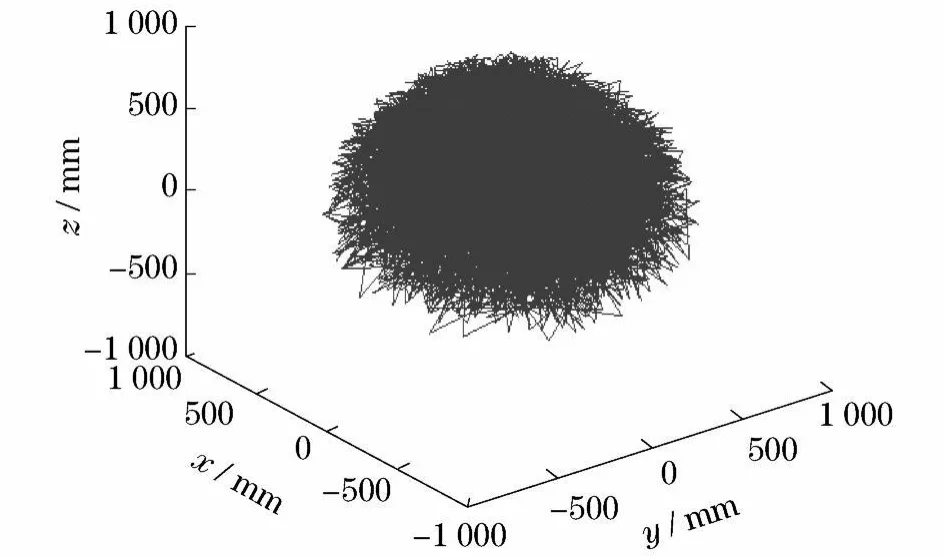
图3 PowerCube模块化机器人工作空间Fig.3 Workspace of PowerCube modular robot

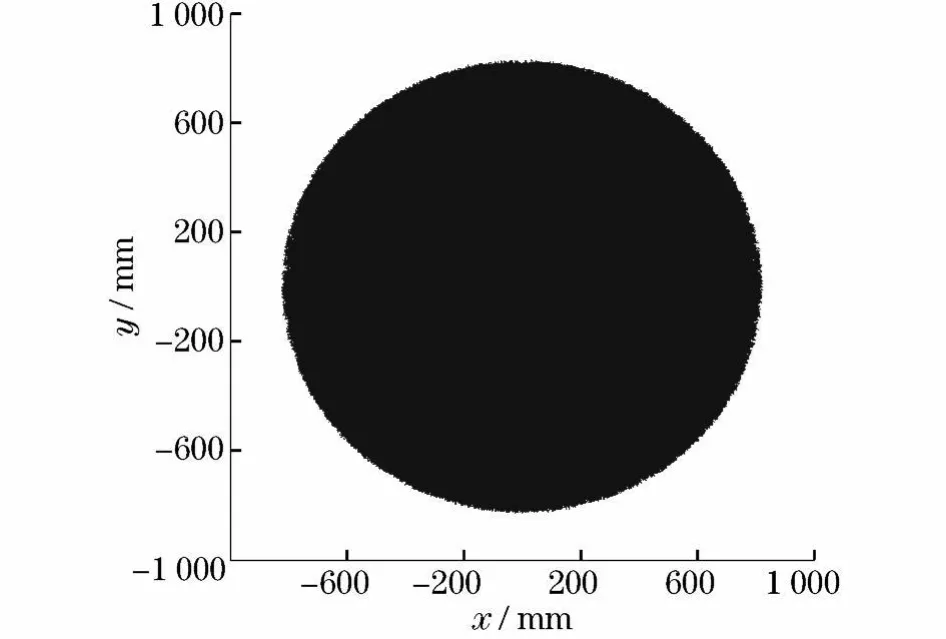
图4 xOy平面投影图Fig.4 xOy projected planform

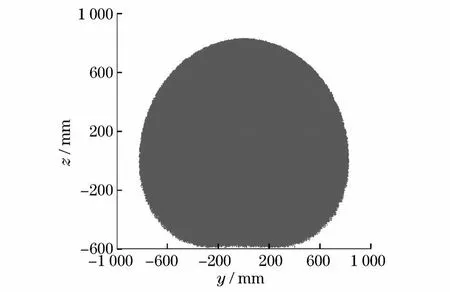
图5 yOz平面投影图Fig.5 yOz projected planform

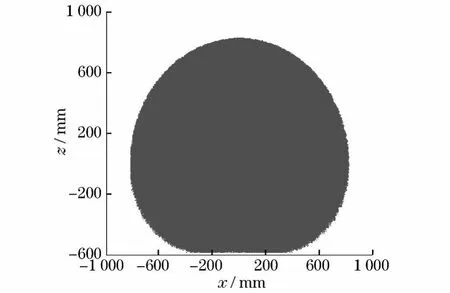
图6 xOz平面投影图Fig.6 xOz projected planform

3.2 分组解析法

分组解析法特别适合于自由度≤6的机器人工作空间的求解.将模块化机器人的前3杆划为一组,在第三杆上设置参考点P3,可求得P3在基坐标系中的工作空间的界限曲面.同时,将模块化机器人的另外3杆划为另一组,在第六杆上设置参考点P6,最终用求解双参数曲面族的包络面公式求出P6在基坐标系中所形成的工作空间.可见,求工作空间的问题可以归结为求曲面族和曲线族的包络问题[8].

设有曲面∑,其方程为(用向量方程表示)

式中:r是曲面∑的数学表达式;u,v是曲面的几何参数.该曲面以β为参数运动,得曲面族为

利用分组解析法并结合PRO-E绘制模块化机器人的工作空间.图7为工作空间半剖面,图8为工作空间轴剖线.

图7 模块化机器人工作空间半剖面Fig.7 Workspace of modular robot

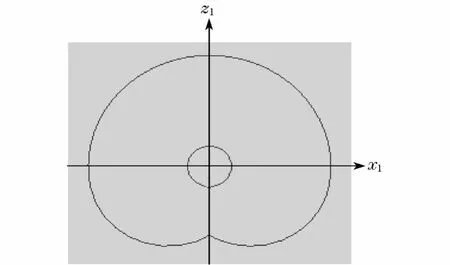
图8 工作空间轴剖线Fig.8 Hatching line of workspace

工作空间的极限位置可以转化为数学规划和优化问题来求得,工作空间各极限位置如表2所示.

表2 模块化机器人工作空间极限位置Tab.2 Limit position of workspace for modular robot

实际计算中,目标函数里并未出现关节变量q6,故未列入表中.某些关节变量在极限位置时的值并不唯一.

4 结论

通过蒙特卡罗数值法和分组解析法计算PowerCube模块化机器人的工作空间,并分别绘制了模块化机器人的工作空间.比较2种方法所产生的图形,可以得出:

(1)将图3和图7进行比较,可以看出,模块化机器人的工作空间由一近似的椭球体构成.再将图6和图8进行比较,可以看出,2种方法所得到的图形轮廓大体上一致.这说明了各方法分析的正确性,也说明了所绘制的模块化机器人工作空间的正确性,为模块化机器人动力学控制和运动规划的深入研究打下了基础.

(2)蒙特卡罗方法算法简单,表达直观,但所得到的工作空间图形轮廓相比之下不很清晰,带有毛刺.这是因为蒙特卡罗法是采用随机抽样组成关节变量组合来计算三维空间点,与实际的工作空间边界具有一定的误差,产生的工作仅仅是近似的工作空间.机构的特性不能很好地描述,细节性的问题很难表示出来.

(3)分组解析法能得到准确、清晰的工作空间.但分组解析法推导过程相对繁琐复杂,对于自由度大于6的模块,不宜使用该方法.

因此,在模块化机器人工作空间计算时,应结合2种方法的优点,才能对模块化机器人的工作空间有一个全面的了解.

[1]姜涛,陆敏恂,徐宝富,等.智能投篮机器人的设计[J].中国工程机械学报,2004,2(3):324-327.JIANG T ao,LU Minxun,XU Baofu,et al.Design of basketball intellectual robot[J].Chinese Journal of Construction Machinery,2004,2(3):324-327.

[2]周爱国,邢洁,陆敏恂.双足机器人的动力学分析与仿真[J].中国工程机械学报,2006,4(2):178-182.ZHOU Aiguo,XING Jie,LU Minxun.Dynamic analysis and simulation of the biped robot[J].Chinese Journal of Construction Machinery,2006,4(2):178-182.

[3]杜启联,余跃庆,张绪平.PowerCube模块化机器人实验系统的研究与开发[J].机械设计与研究,2004,20(6):16-18.DU Qilian,YU Yueqing,ZHANG Xuping.Research and development for experiment system of PowerCube modular robot[J].Journal of Machine Design and Research,2004,20(6):16-18.

[4]赵杰,王卫忠,蔡鹤皋.可重构机器人工作空间的自动计算方法[J].天津大学学报,2006,39(9):1082-1087.ZHAO Jie,WANG Weizhong,CAI Hegao.Algorithms for automatically determining workspace of reconfigurable robots[J].Journal of Tianjin University,2006,39(9):1082-1087.

[5]蔡蒂,谢存禧,张铁,等.基于蒙特卡洛法的喷涂机器人工作空间分析及仿真[J].机械设计与制造,2009(3):161-162.CAI Di,XIE Cunxi,ZHANG T ie,et al.Study on workspace analysis and simulation of 6-DOF painting robot based on monte-carlo method[J].Machinery Design&Manufacture,2009(3):161-162.

[6]赵燕江,张永德,姜金刚,等.基于Matlab的机器人工作空间求解方法[J].机械科学与技术,2009,28(12):1657-1661.ZHAO Yanjiang,ZHANG Yongde,JIANG Jingang,et al.A method for solving robot workspace based on Matlab[J].Mechanical Science and Technology,2009,28(12):1657-1661.

[7]石磊,苏丽颖,余跃庆.模块化机器人双臂协调操作的实验研究[J].西华大学学报:自然科学版,2007,26(5):3-6.SHI Lei,SU Liying,YU Yueqing.Experimental investigation into the coordinated manipulation of a dual-arm modular robot[J].Journal of Xihua University:Natural Science,2007,26(5):3-6.

[8]马香峰.机器人机构学[M].北京:机械工业出版社,1991.M A Xiangfeng.Robot mechanisms[M].Beijing:China Machine Press,1991.