计算阶次分析中的采样率设置准则

杨通强,郑海起,龚烈航,唐力伟

(1.解放军理工大学 工程兵工程学院,江苏 南京 210007;2.军械工程学院一系,河北石 家庄 050003)

当前,阶次分析技术是旋转机械状态监测和故障诊断领域的1种基础性分析方法,应用非常广泛.由于可以避免转速不稳所带来的“频率模糊”现象[1],所以即使最终采用其他信号处理算法,也往往要基于其核心技术——角域采样获得数据,而后进行分析.常用的阶次分析方法有2种:硬件阶次分析法和计算阶次分析法.前者需通过硬件实现同步采样,而后者则通过数值计算方法实现信号的角域重采样,具有采样率设置灵活、成本低、传感器安装方便等优点,应用更为普遍,被近期绝大多数文献[2～4]所采用.

与时域采样类似,角域采样中也不可避免地会遇到采样率不足、采样率过高及抗混滤波器设置等问题,本文依据采样定理,分析了角域采样率的设置原则,给出了计算公式;计算阶次分析实验中既涉及到时域采样又有角域采样.转速变化的影响使得1种采样相对另1种采样必然为变采样率的采样,而跟踪转速变化的变采样率抗混滤波又难以实现,为此本文分析总结了只用1次定带宽抗混滤波——时域抗混滤波,避开角域滤波的采样率设置方法,并通过仿真实验进行了验证说明.

1 计算阶次分析

计算阶次分析法是近年来发展起来的1种先进技术,其主旨在于通过信号处理算法将等时间间隔采样信号转化为等角度采样信号,即同步采样信号.与硬件阶次分析法相比,此方法既可降低成本、放宽传感器安装限制又能提高角域采样率,优点显著.具体实现过程如下:

首先要设定参考轴的角加速模式来确定重采样的时间点.一般认为在1个小的时间段内参考轴作匀角加速运动(特殊情况下加速模式已知的除外),前人[5]的研究证明了该假设的可行性.

在此前提下,参考轴的转角θ可以表达为如下形式:

式中:b0,b1,b2为待定系数;t为时间点.

对等时间间隔采样信号,将3个依次到达的脉冲时间点t1,t2,t3和转角增量Δφ带入式(1),得

由式(2)求出bi(i=0,1,2)后,将其代入(1)式可得

根据式(3)便可求出等角度采样时恒定角增量Δθ所对应的需要插值的时间点.再根据所求出的时间点,利用插值算法对振动信号进行插值,可以求出振动信号角域里对应于采样时间点的幅值,再对其进行快速傅里叶变换(FFT),结果就是重采样后的阶次谱图.

2 角域采样率准则

由上节可见,角域重采样技术是计算阶次分析的关键步骤,若该环节出现误差必将对后续分析产生较大影响,因此为了避免阶次域混迭现象,本节重点研究阶次采样率问题.

由于阶次分析与传统频率分析相比,基本数学变换理论依据均为傅里叶变换,只是分析对象由时域换为角域,所以下面类比时域采样定理推导过程分析角域采样准则:

设1个上限阶次为Om的有限带宽的连续角域信号 x(θ),其阶次域表达式为X(O),且当｜O｜＞Om时,X(O)=0,如图1a,b所示.若用1个脉冲序列δT(θ)去乘 x(θ)时,则其乘积 x(θ)δT(θ)是1个间距为 Tθ的脉冲序列,其在相应的瞬时具有与x(θ)值相等的强度,如图1c,e所示,即取样后的信号为

均匀脉冲序列δT(θ)的傅里叶变换δT(O)为

式中:δOs(O)为频域内以Os为周期的均匀脉冲序列.δT(O)也是一个均匀脉冲序列,如图1d所示,每个脉冲的间隔为

根据卷积定理,采样后信号 xs(θ)的傅立叶变换为 Xs(O),如图1f所示,即

它是由X(O)与脉冲序列OsδOs(O)卷积而得,即原信号 x(θ)的频谱每隔Os=2π/Tθ周期性地重复1次.显然,只有满足

时Xs(O)才能包含x(θ)的全部信息,周期出现的X(O)才不会产生首尾重叠现象,即不混迭.

综上可见:1个在阶次Om以上无阶次分量的有限带信号,可以由它在小于或等于π/Om均匀角度间隔Δθ上的取值唯一地加以确定.即

以上说明,如果在某一阶次Om以上x(θ)傅里叶变换等于零时,则关于 x(θ)的全部信息均包含在它的采样间隔小于π/Om的均匀采样信号里.信号 x(θ)每隔Δθ角度被采样1次,或者说以大于或等2Om采样率进行采样,这些采样值 x(n)包含了 x(θ)在每一个θ角度值的信息.

3 角域重采样实验采样率设置方法分析

图1 角域采样原理Fig.1 Effect in the order domain of sampling in the angular domain

设某转速为ω的转速机械的时域信号为X(ω,t),对于变转速机械,ω也是时间t的函数.对其进行时域采样,采样频率为fs,则采样脉冲间隔为

时域采样信号为

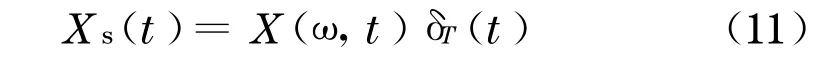
式中:δT(t)为以T为周期的单位冲击信号序列.根据采样定理,抗混滤波器的上限频率为

那么,在角域内可将此信号看作变采样率采样信号,且角域采样率随ω的变化而变化:

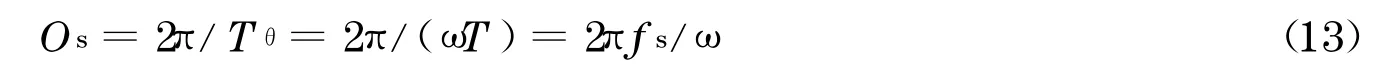
相应地,角域内原来的时域抗混滤波器的上限阶次也成为ω的函数,为

因此,欲对时域采样信号进行采样阶次为定值O—s的重采样时,首先要对该时域信号进行时域内的跟踪滤波.根据式(8)得O—m=O—s/2,代入式(14)可得上限频率为

以上分析可见,计算阶次分析实验中既涉及到时域采样又有角域采样.转速变化的影响使得1种采样相对另1种采样必然为变采样率采样,而跟踪转速变化的变采样率抗混滤波又难以实现,下面分析总结只用1次定带宽抗混滤波——时域抗混滤波,避免跟踪抗混滤波的采样率设置方法.

(1)由式(15)及时域采样定理,欲保留所需信息,则 fs需满足

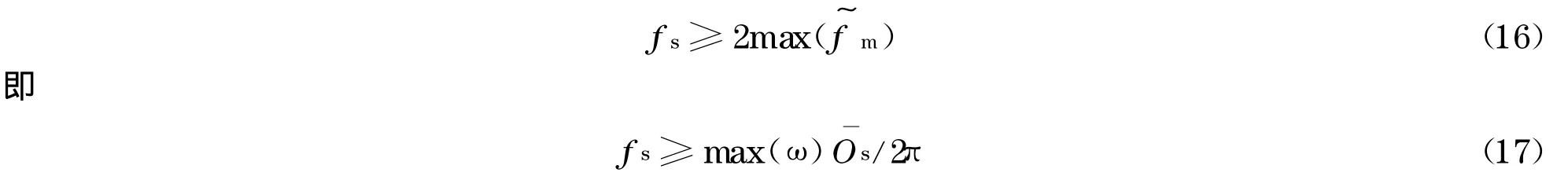
表明时域采样率应根据最大转速和预期采样阶次来设置,否则会采样不足.

(2)由式(13)知,在角域重采样时,若不进行抗混滤波,为了满足采样准则,则需Os≥max(2πfs/ω)即

4 算例分析

设某变转速信号y为

式中:ω=20t,t=[1,3].

从信号表达式可见其中仅含有轴频的15阶信息.假设欲采用先时域采样,再作角域重采样和阶次分析来分析该阶信息,即Om=15,O—s≥2Om,取其最小值O—s=2Om代入式(17),确定时域采样频率为 fs≈287 Hz.现分别采用2种时域采样率对其进行采样,结果如图2和图3.图2为采样率满足该条件时信号采样结果,图中信号表现为规则的扫频信号,准确地表达了原信号信息;图3为根据平均转速计算所得采样率245 Hz时的采样结果,显然信号由于采样率不足而产生了严重失真.说明了式(17)的正确性.

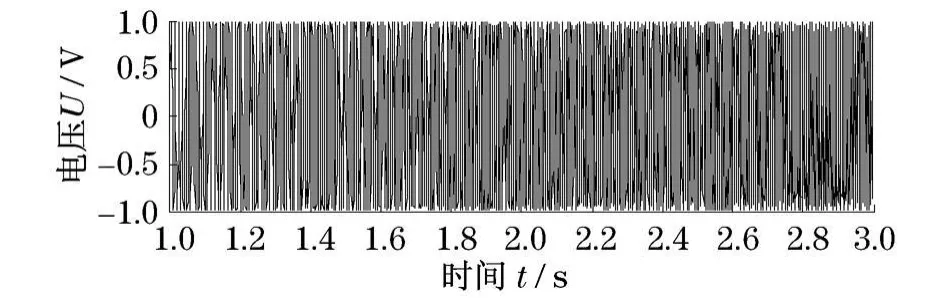
图2 采样率大于287 Hz时的采样信号Fig.2 Sampled signal when the sampling frequency is above 287 Hz

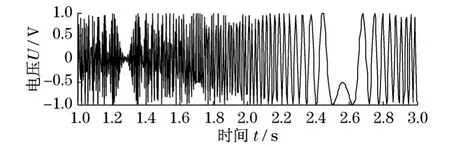
图3 采样率为245 Hz时的采样信号Fig.3 Sampled signal when the sampling frequency is 245 Hz

下面对式(10)进行验证:

设上算例信号中含有40阶高阶信号,则信号表达式变为

仍以分析15阶信息为目的,由式(18)得:min(O—s)≈90阶.

图4 正常重采样时的阶次谱Fig.4 Order spectrum of the normal sampled signal

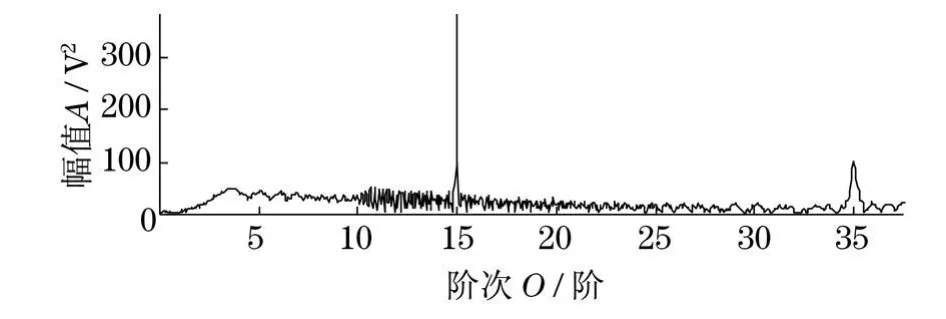
图5 采样率过低时的阶次谱Fig.5 Order spectrum of the undersampled signal

5 结论

计算阶次分析技术作为旋转机械状态监测和故障诊断领域的1种基础性分析方法,应用日益广泛.角域重采样是计算阶次分析的关键步骤,其采样精度将直接影响分析结果.角域采样率的设置需满足Os≥2Om;计算阶次分析实验中,转速变化的影响使得1种采样相对另1种采样必然为变采样率采样.本文分析总结了只用1次定带宽抗混滤波——时域抗混滤波,避开变带宽跟踪滤波的采样率设置方法:时域采样率应根据最大转速和预期采样阶次来设置,fs≥max(ω/2π,否则采样不足;角域重采样率则应根据最小转速和时域采样率来确定,Os≥2πfs/min(ω),否则会产生阶次混迭.

[1]朱继梅.非稳态振动信号分析[J].振动与冲击,2000,19(1):86-87.ZHU Jimei.Nonstationary vibration signal analy sis[J].Journal of Vibration and Shock.2000,19(1):86-87.

[2]郭瑜,秦树人.旋转机械非稳定信号的伪转速跟踪阶比分析[J].振动与冲击,2004,23(1):61-64.G UO Yu,QING Shuren.Pseudo-speed tracking order analysis for non-stationary vibration signal of rotating machinery[J].Journal of Vibration and Shock.2004,23(1):61-64

[3]杨通强,郑海起,唐力伟.基于角域平均和倒阶次谱分析的齿轮箱故障诊断[J].机械科学与技术,2005,25(4):452-454.YANG T ong qiang,ZHENG Haiqi,TA NG Liwei.Gearbox fault diagnosis based on angle domain averaging and order cepstrum analysis[J].Mechanical Science and Technology.2006,25(4):452-454

[4]李辉 郑海起唐力伟.瞬时频率估计的齿轮箱升降速信号阶次跟踪[J].振动、测试与诊断,2007,27(2):125-128.LI Hui,ZHENG Haiqi,TANG Liwei.Order tracking of speed-up signal for gearbox based on instantaneous frequency estimation[J].Journal of Vibration,Measurement&Diagnosis.2007,27(2):125-128.

[5]F YFE K R,MUNCK E D S.A naly sis of computed order tracking[J].Mechanical Sy stems and Signal Processing,1997,11(2):187-205.