蜂窝体胞尺寸对夹芯板性能的影响研究

孙士平， 赖余东

(南昌航空大学航空制造工程学院，南昌330063)

蜂窝夹芯板是由上下蒙皮和周期性多孔蜂窝夹芯构成的轻质结构材料，具有高比刚(强)度、隔热、减振等优异性能，被广泛应用于航空、航天等工程领域［1］。对于开孔蜂窝构成夹芯板结构，根据蜂窝开孔方向与蒙皮法线方向的相对位置关系，可分为两类：一类是利用开孔蜂窝的面内性能，实现夹芯板结构减震吸能、散热等多功能要求，其蜂窝体胞开孔方向与蒙皮法向相互垂直;另一类是利用周期性蜂窝材料作为轻质夹芯来实现减重、承载和增强稳定性等功能要求，其蜂窝体胞开孔方向与蒙皮法向相互平行。由于多孔夹芯有限元直接离散分析造成夹芯结构建模复杂和计算成本过高，国内外学者对多孔夹芯材料性能的预测计算开展了大量研究，提出能量法［2］、Gibson公式［1］及其修正法［3］、均匀化方法［4］等多种简洁有效的周期性多孔蜂窝材料等效性能计算方法，有效地促进了蜂窝夹芯结构的应用与发展。

然而，这些方法存在一个共同特点就是无法反映蜂窝体胞的尺寸效应，即计算获得的等效性能只与蜂窝体胞的构型和材料组分相关，而与蜂窝体胞的尺寸无关。以均匀化方法为例，当蜂窝体胞尺寸与宏观结构尺寸处在同一数量级范围，不符合其理论前提假设要求的蜂窝体胞尺寸远小于宏观结构尺寸时，均匀化等效后的计算结果将偏离真实结果。目前，对于蜂窝尺寸效应的研究有如下结果：Andrews［5］，Onck［6］，Tantikom［7］等人选用六边形、圆管形等不同构型蜂窝材料通过实验测试和数值计算分析，发现蜂窝体胞尺寸与试件材料尺寸相当时，实验测试结果依赖于蜂窝体胞尺寸，揭示了尺寸效应的存在及其影响;阎军［8］等分析计算了二维周期性点阵类桁架材料的等效性能，比较验证了Dirichlet型、Neumann型边界条件下的尺寸效应规律;戴高明［9，10］等人基于能量法研究了二维周期性蜂窝材料和夹芯梁的蜂窝尺寸影响; zhang［11，12］等人开展了考虑尺寸效应影响的二维夹芯结构刚度优化设计。最近，戴高明［13］等人基于能量法研究了夹芯梁自由振动频率的尺寸效应问题。

综上所述，已有的夹芯蜂窝材料尺寸效应研究均以周期性开孔蜂窝体胞为对象，研究二维蜂窝材料面内性能随蜂窝尺寸变化的规律。而对于第二类夹芯板结构，其性能不仅与蜂窝体胞面内性能相关，还受蜂窝体胞面外性能以及蒙皮的影响，因此，有必要进一步研究三维蜂窝体胞尺寸对夹芯板结构性能(如刚度、频率等)的影响。为此，本研究首先建立蜂窝夹芯板三维有限元模型，以夹芯均匀化等效后的夹芯板模型计算结果为基准，采用夹芯板结构直接有限元离散的计算结果与均匀化等效的计算结果的比值——尺寸影响因子来量化蜂窝尺寸对夹芯板性能的影响程度，开展三维蜂窝体胞尺寸对第二类夹芯板结构整体刚度性能、自由振动频率的影响研究，并分析比较在不同边界条件下、不同构型时蜂窝尺寸对夹芯板结构性能的影响规律。

1 均匀化方法与尺寸效应

均匀化方法是目前预测周期性材料等效性能的一种常用计算方法。该方法基于严格的数学推导描述了蜂窝体胞等效性能与其组分材料和构型的内在关系。当蜂窝体胞尺寸相对于宏观结构尺寸趋于无限小时，蜂窝体胞等效弹性张量的计算表达式为：

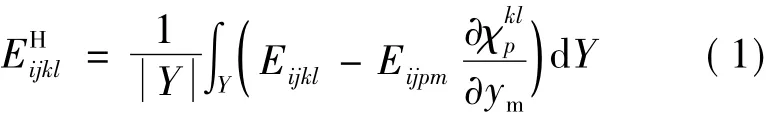
式中χkl为第kl工况下的弹性位移场，Eijkl为组分材料的弹性张量为蜂窝体胞的体积。

式(1)表明，基于均匀化方法计算得到的蜂窝体胞等效弹性性能仅与材料组分和材料空间分布相关，而与体胞的空间尺寸没有关联，因此，对于图1所示相同组分不同尺寸的蜂窝体胞构成夹芯材料，基于均匀化理论都具有相同的等效性能。实际上，图1中不同蜂窝尺寸的夹芯材料其力学响应是不一样的，与均匀化等效模型计算结果是存在差异的，这种差异称为尺寸效应。图1中M=2×2×2表示该夹芯材料在X1，X2，X3三个方向分别包含体胞数量的乘积，即包含的总体胞数量。

图1 夹芯均匀化等效示意图Fig.1 A honeycomb core with different size cells

工程设计中，常根据夹芯板结构的不同性能要求，选择不同组分和构型的蜂窝夹芯材料。面对同种构型和组分的蜂窝夹芯材料，由于工业供给的规格存在多样性，其选用就存在随意性，这必然会影响夹芯板结构的设计精度和制造成本。因此，有必要开展蜂窝尺寸对夹芯板性能的影响研究，进一步完善夹芯板结构的设计方法。

2 尺寸影响评价

对蜂窝体胞尺寸效应的评价，根据研究内容的不同，通常会采用规范化弹性模量［5］、规范化应力 、挠度 以及频率 等不同参数随宏-细观尺度比值变化的关系来描述尺度效应的影响。

由于夹芯板结构性能分析涉及蒙皮和夹芯的几何构成、静力或动力分析类别以及不同边界条件等多种情况，因此，需要有一个统一的指标来描述蜂窝尺寸变化对夹芯板不同性能的影响规律，以便直观的评价比较影响程度。

定义“尺寸影响因子”来描述蜂窝尺度对夹芯板性能的影响，该因子为夹芯板结构整体性能φ (如刚度K、频率f等)与均匀化等效夹芯构成夹芯板结构等效性能φH的比值，其表达式可写为：

式中的下标φ描述具体的评价性能，如K，f等。

显然，这是一个无量纲指标，为评价不同情况下夹芯板结构受蜂窝尺寸的影响提供了一个判据，当αφ偏离1越远，表明蜂窝尺寸的影响越大，而当αφ→1时，说明蜂窝尺寸的影响逐渐减小，实际模型计算结果趋近均匀化等效模型计算结果。

对于结构刚度K，通常用结构柔顺度C(结构变形能)来描述，概念上两者互为倒数关系，即将刚度转化为柔顺度表达，则有：

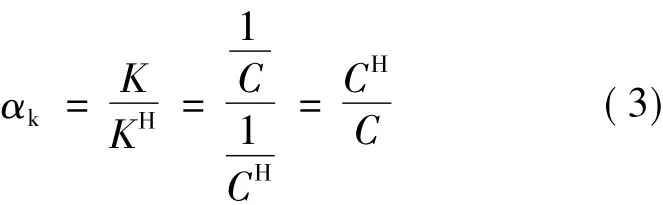
图2 夹芯结构不同构型夹芯等效示意图Fig.2 Sandwich panel with the different cell configurations and with the homogenized core

考虑图2所示夹芯板，其上、下蒙皮厚度为lf，夹芯尺寸为li(i=1，2，3)，夹芯蜂窝体胞尺寸为si，则夹芯板厚度为(l+2l)，宏细观尺度比

3f存在αφ=f(ηi)(i=1，2，3)。对于三维开孔蜂窝体胞，当面内(图2中Y1-Y2平面)尺寸等比例缩放时，其构型和组分保持不变，而面外(图2中Y3方向)尺寸的变化也不会影响其均匀化等效性能。因此当蜂窝构型和夹芯尺寸确定后，必存在η2=ψ(η1)，推导得到αφ=F(η1)，即可以只用η1来描述开孔蜂窝尺寸对夹芯板性能的影响。图2中DH，ρH分别表示夹芯等效后的等效弹性矩阵和等效密度。

3 计算分析

假定图2中夹芯板尺寸为288mm×166mm× 9.4mm，其上、下蒙皮厚度lf=0.7mm，则夹芯材料尺寸为l1×l2×l3=288mm×166mm×8mm。这是一薄板结构，其中铝夹芯的材料体份比Vf=30.56%，弹性模量E1=70GPa，泊松比ν1=0.3，密度ρ1= 2700kg/m3;铝合金蒙皮材料E2=155GPa，ν2=0.3，ρ2=2700kg/m3。采用ANSYS进行夹芯板建模分析，在夹芯板实际模型中，夹芯蜂窝、上下蒙皮均采用壳单元;在夹芯板等效模型中，上下蒙皮采用壳单元，等效夹芯采用三维实体单元。三种相同组分(30.56%)不同构型的夹芯蜂窝体胞参数见表1，三种构型蜂窝具有相同的等效密度 ρH=ρ1×Vf= 825.12kg/m3，其等效弹性性能采用均匀化求解［14］。计算中分别取 S1=96mm，48mm，24mm，12mm，6mm，相应η1=3，6，12，24，48。

3.1 静力分析

以图3的三种典型边界为例，计算比较六边形、三角形、正方形构型蜂窝尺寸变化对夹芯板刚度性能的影响规律。载荷F=1000N，夹芯均匀化等效后的夹芯板在三种工况下的等效柔顺度值如表2所示。不同工况和不同蜂窝夹芯板的尺寸影响因子αk变化趋势如图4～图6所示。

表1 不同构型蜂窝参数Table 1 Parameters of different cells

图3 三种典型工况示意图Fig.3 Three typical loading cases (a)loading case A; (b)loading case B;(c)loading case C

表2 不同构型蜂窝夹芯均匀化等效后的夹芯板柔顺度Table 2 Compliances of sandwich panels with the homogenized cores of different cells

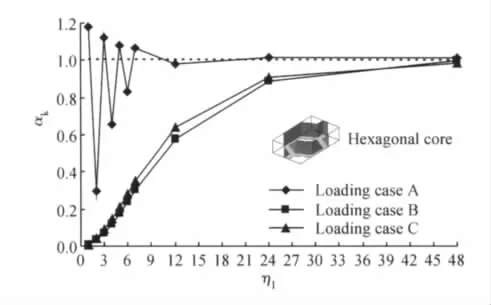
图4 六边形蜂窝尺寸影响因子与宏细观尺寸比的关系曲线Fig.4 Curves of size influencing index vs the ratio of macro size to meso size for hexagonal core

由图4、图5、图6可以看出，夹芯板刚度性能受蜂窝尺寸的影响明显。在不同工况边界下，随着宏细观尺寸比η1的增大(即蜂窝体胞尺寸减小)，蜂窝尺寸对夹芯板刚度性能的影响逐渐减小(即αk→1)，总体上，当η1≥12后，蜂窝尺寸的影响变得较为平缓。从曲线波动幅度看，图5显示三角形蜂窝夹芯板刚度性能受蜂窝尺寸的影响相对较小，而图4说明六边形蜂窝夹芯板刚度性能受蜂窝尺寸的影响较显著，且影响的消失较缓慢。另外，图4的工况A，尺寸影响因子变化曲线表现为震荡收敛，其原因如图7所示，当X2方向包含偶数个体胞时，载荷作用点位于蜂窝空隙中间(图7a);当X2方向包含奇数个体胞时，载荷作用点位于蜂窝壁上方(图7b)，随着蜂窝尺寸的减小，载荷作用点在两者间摆动，最后逐渐减小至忽略。可见蜂窝尺寸与宏观结构尺寸相当时其对结构刚度性能影响较大。图6显示正方形蜂窝夹芯板在不同工况下受蜂窝尺寸影响的程度存在较大差别。

图7 工况A载荷作用位置与六边形蜂窝的相对关系示意图Fig.7 Illustration of relationship between loading point and cell configuration for different cell size under loading case A (a)even cells in X2direction (b)odd cells in X2direction

另一方面，在工况A时，三种构型蜂窝夹芯板的尺寸影响因子αk随宏细观尺寸比η1变化的收敛速度基本一致，但当η1较小时三角形、四边形蜂窝尺寸的影响明显小于六边形蜂窝尺寸的影响;工况B时，三种构型蜂窝夹芯板的刚度性能受蜂窝尺寸的影响较明显，只有尺寸影响因子的收敛速度存在差别，六边形蜂窝收敛缓慢而四边形蜂窝收敛较快。而工况C时，三角形和四边形蜂窝在η1较小时，存在非单调的波动变化，其原因是η1较小时，四边形蜂窝夹芯板在X2方向上包含的不完整蜂窝体胞(即η2不是整数)以及三角形蜂窝夹芯板在X2方向上体胞分布的不对称性对夹芯板刚度的影响较大，随着蜂窝尺寸的减小，不完整(或不对称分布)体胞的影响逐渐减小，最后趋于1。

图8为正方形蜂窝夹芯板在尺寸假定为288mm×288mm×9.4mm时，三种工况下尺寸影响因子的变化趋势，此时夹芯板在两方向(X1，X2)上均恰好包含整数个蜂窝体胞且η1=η2。与图6相比，虽然图8描述的蜂窝尺寸影响趋势未变，但工况C时，尺寸影响因子表现为单调递减，这说明当在蜂窝尺寸较大时，工况C边界增加了蜂窝尺寸影响的复杂性。

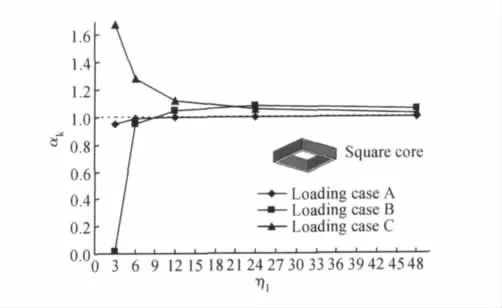
图8 正方形蜂窝尺寸影响因子与宏细观尺度比的关系曲线Fig.8 Curves of size influencing index αkvs the ratio of macro size to meso size η1for square core

3.2 自由振动分析

以图3所示夹芯板的两种位移边界(工况A和工况B)为例，夹芯板尺寸仍假定288mm×166mm× 9.4mm，计算比较六边形、三角形、正方形蜂窝尺寸变化对夹芯板一阶自由振动频率的影响。表3为夹芯均匀化等效后夹芯板的等效一阶频率。图9、图10给出了两种工况下尺寸影响因子αf的变化趋势。

表3 不同构型夹芯均匀化等效后的夹芯板一阶频率Table 3 The first order frequency of sandwich panels with homogenized cores of different cells

图9、图10说明夹芯板自由振动一阶频率存在尺寸效应。从图中可以看到，工况A时各种构型蜂窝尺寸变化对夹芯板一阶频率的影响都小于工况B;工况B情况下，不同构型蜂窝对应的尺寸影响因子却具有一致的变化趋势。另外，在两种工况下，六边形蜂窝夹芯板的一阶频率受蜂窝尺寸影响较小，而四边形蜂窝夹芯板受蜂窝尺寸影响较大，这与3.1节夹芯板刚度性能的影响规律存在差异。

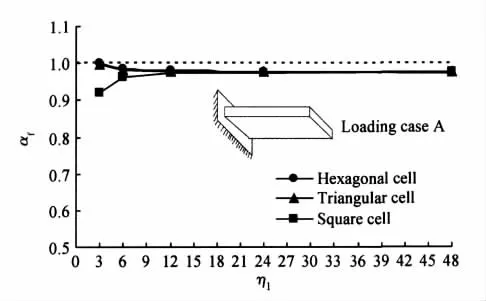
图9 工况A时尺寸影响因子与宏细观尺度比的关系曲线Fig.9 Curves of size influencing index αfvs the ratio of macro size to meso size η1under loading case A

3.3 讨论

表2、表3的计算数据表明：夹芯板的刚度与一阶频率成正比，在相同重量约束下，不同构型夹芯板的性能存在一定差别，有必要根据具体的载荷工况开展夹芯蜂窝构型的优选或优化设计，以改进夹芯板性能，提高结构效率。

图10 工况B时尺寸影响因子与宏细观尺度比的关系曲线Fig.10 Curves of size influencing index αfvs the ratio of macro size to meso size η1under loading case B

六边形蜂窝夹芯板的刚度性能受蜂窝尺寸变化的影响明显强于蜂窝尺寸变化对频率的影响，而四边形、三角形蜂窝夹芯板的刚度性能、一阶频率受蜂窝尺寸变化的影响程度基本相同。这种现象增加了多功能夹芯板设计的难度，需要根据具体的性能指标调整优化策略。

相比于文献［10］给出的二维三角形、四边形蜂窝单调趋于均匀化解的尺寸影响变化趋势和六边形蜂窝非单调趋于均匀化解的变化趋势，三维蜂窝尺寸对夹芯板性能的影响则不具备这种规律性，因涉及蒙皮、边界条件等因素而表现复杂。

已有计算结果显示：总体上，当宏细观尺寸比大于12时，实际模型的计算结果(刚度、频率)才较平稳的逐渐接近均匀化等效模型的计算值，因此，可根据具体的设计精度要求，忽略蜂窝尺寸的影响，采用均匀化等效模型来简化计算。但对于六边形蜂窝构型夹芯板，处于工况B和工况C状态，当宏细观尺寸比大于24时，其计算结果的尺寸影响才逐渐趋于平缓减小。

4 结论

(1)蜂窝夹芯板的刚度性能与一阶频率都存在尺寸效应。

(2)当夹芯板与蜂窝的尺寸比值η1≥12后，蜂窝尺寸的影响程度平缓减弱，实际模型的计算结果逐渐趋同于均匀化计算值，说明当宏观夹芯包含足够多的蜂窝体胞时，采用均匀化方法开展夹芯板结构的分析计算是有效的。

(3)当η1＜12时，蜂窝尺寸对夹芯板性能的影响明显，且影响程度和趋势与不同边界工况、不同蜂窝构型显著相关。

［1］GIBSON L J，ASHBY MF.Cellular Solids：Structure and Properties：2nded［M］.UK：Cambridge University Press，1997.

［2］HOHE J，BECKER W.A mechanical model for two dimensional cellular sandwich cores with general geometry［J］. Computational Materials Science，2000，19：108～115.

［3］富明慧，尹久仁.蜂窝芯层的等效弹性参数［J］.力学学报，1999，31(1)：113-118.

［4］HASSANI B，HINTON E.A review of homogenization and topology optimization II：Analytical and numerical solution of homogenization equations［J］.Computers＆Structures，1998，69：719-738.

［5］ANDREWS EW，GIOUX G，ONCK P，et al.Size effects in ductile cellular solids.Part II：Experimental results［J］. International Journal of Mechanical Sciences，2001，43：701-713.

［6］ONCK P R，ANDREWS E W，GIBSON L J.Size effects in ductile cellular solids.Part I：Modeling［J］.International Journal of Mechanical Sciences，2001，43：681-699.

［7］TANTIKOM K，AIZAWA T，MUKAI T.Symmetric and asymmetric deformation transition in the regularly cellstructured materials.Part I：Experimental study［J］.International Journal of Solids and Structure，2005，42：2199-2210.

［8］阎军，程耿东，刘书田，等.周期性点阵类桁架材料等效弹性性能预测及尺度效应［J］.固体力学学报，2005，26(4)：421-428.

［9］DAI G M，ZHANG W H.Size effects of basic cell in static analysis of sandwich beams［J］.International Journal of Solids and Structure，2008，45，2512-2533.

［10］戴高明，张卫红.周期性多孔材料等效杨氏模量的尺度效应研究［J］.中国科学G辑，2009，52(8)：1262～1270.

［11］ZHANG W H，SUN S P.Scale-related topology optimization of cellular materials and structures［J］.International Journal for Numerical Methods in Engineering，2006，68，993-1011.

［12］张卫红，孙士平.多孔材料/结构尺度关联的一体化拓扑优化技术［J］.力学学报，2006，38(4)：522-529.

［13］DAI G M，ZHANG W H.Cell size effects for vibration analysis and design of sandwich beams［J］.Acta Mechanica sinica，2009，25：353-365.

［14］邱克鹏，张卫红，孙士平.蜂窝夹层结构等效弹性常数的多步三维均匀化数值计算分析［J］.西北工业大学学报，2006，24(4)：514-518.