扇形凹穴型微通道液体流动与传热特性的数值模拟

柴 磊，夏国栋，周明正，杨瑞波

(北京工业大学环境与能源工程学院，100124北京，chailei@emails.bjut.edu.cn)

随着微机电系统的发展及微加工技术的日臻完善，一些基于不同传热机理、设计新颖、性能优越的微型热沉不断涌现，扇形凹穴型微通道热沉便是其中的一种.扇形凹穴的设计，使微通道分为等直径段和弧形段，流体在反复改变速度和压力梯度下流动，使边界层不断地中断和再发展.同时传热面积增大，传热效果显著提高.因此，扇形凹穴型微通道热沉在强化微尺度传热方面具有明显的优势.微通道热沉的定义最早由 Tuckerman等［1］于1981年提出，其设计的微通道热沉最大热流密度可达7.9 MW/m2，而热沉底面与进口流体温差不超过71℃.文献［2-4］研究了微通道内流体的流动特性.文献［5-7］研究了微通道内流体的传热特性，并对各自的微通道热沉几何结构进行优化设计.文献［8-10］研究了粗糙度对流体流动和传热特性的影响.文献［11-13］研究了流体物性随温度变化对流体流动和传热特性的影响.然而关于微通道内流体流动与传热特性的研究主要集中在等截面微通道范畴内，而对于截面周期性变化的凹穴型微通道尚缺乏相关的报道.本文采用Fluent三维双精度和非耦合隐式求解器以及SIMPLEX算法模拟扇形凹穴型微通道(Fanshaped reentrant cavities micro-channel，FRCMC)热沉和等截面矩形微通道(Conventional rectangular micro-channel，CRMC)热沉内流体的流动和传热特性.采用有限体积法求解N-S方程和能量方程，得到流体的流动和传热特性参数.

1 数值模拟

1.1 数值模型

扇形凹穴型微通道和等截面矩形微通道热沉结构及尺寸如图1所示.单个通道等直径段处宽度a均为0.1 mm，高b为0.2 mm，微通道长L为10.15 mm.扇形凹穴张角为 120°、半径为0.1 mm，间距为0.29 mm.扇形凹穴型微通道与等截面矩形微通道相等，其水力直径取等直径段值0.133 3 mm，微通道材料均为硅，流体工质采用纯水.基于对称性的考虑，所取基本单元如图2所示，浅色为流体流动区域.

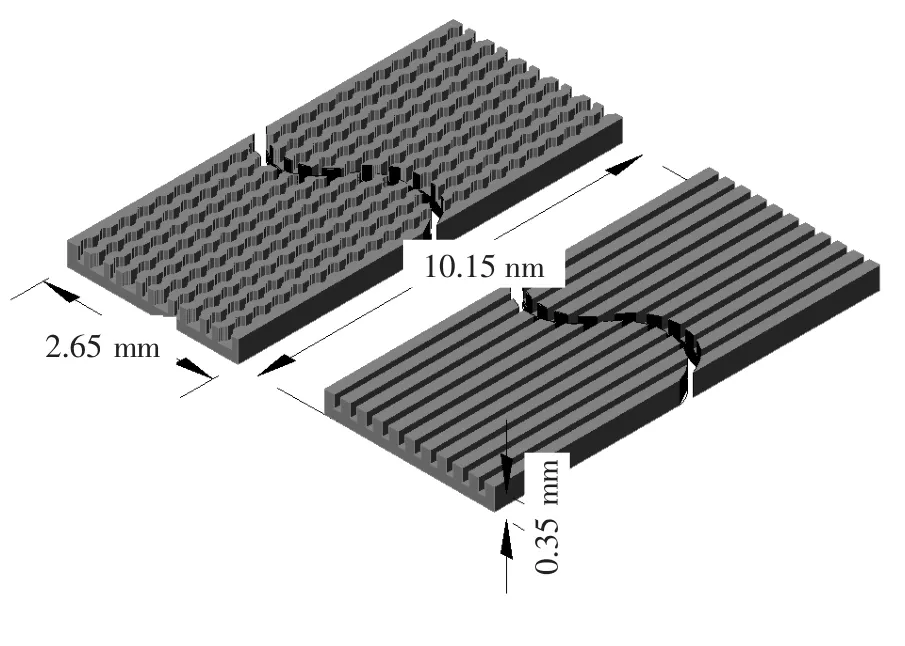
图1 微通道热沉结构示意图

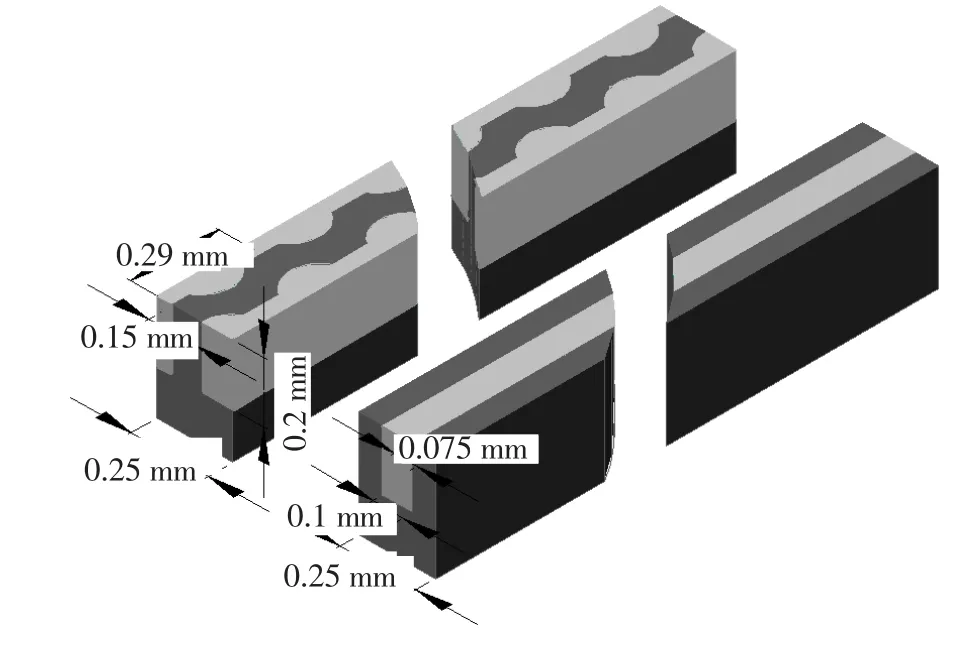
图2 基本计算单元示意图

为简化计算，作如下假设:流体为三维稳态不可压缩层流;流体黏度随温度分段线性变化，其他物性参数为常数;固体的各物性参数为常数;忽略体积力;N-S方程仍然适用.则单相流体的连续性方程、动量方程、能量方程分别为

式中:φ为粘性耗散项，表示流体变形时粘性应力的作功功率，这部分机械能不可逆的转变成热能.其表达式为

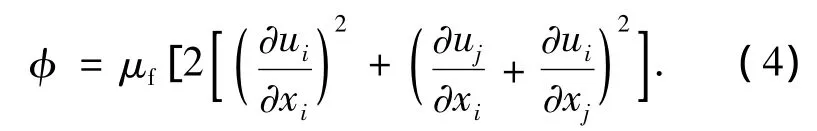
对于构成通道的硅基固体区域，能量方程为

1.2 边界条件

液体和固体的接触表面没有速度滑移，微通道的进口设为速度边界条件，出口设为压力出口边界条件，设出口压力为零.选取的计算单元两侧为对称边界条件，其对称面的法向速度为零，所有变量的法向梯度为零.假设通道基座底面有均匀定热流q，作为由加热膜产生的热量，其余表面均为绝热.流体的动力黏度值见文献［14］.

1.3 数值方法

扇形凹穴型微通道网格结构的复杂性，增加了划分的难度，网格的质量决定了数值计算的准确性，所以应对网格独立性进行检测.扇形凹穴型微通道计算单元进口速度u=4 m/s时，网格数分别为8.7万、9.8万、21.4万、32.9万与网格数为55万的的计算单元测得的微通道进出口压降最大误差分别为 8.73%、4.65%、2.38%、0.56%.因此，扇形凹穴型微通道计算单元取网格数为32.9万个.本文数值模拟的等截面矩形微通道基本单元的网格数为32.4万个.收敛的标准为

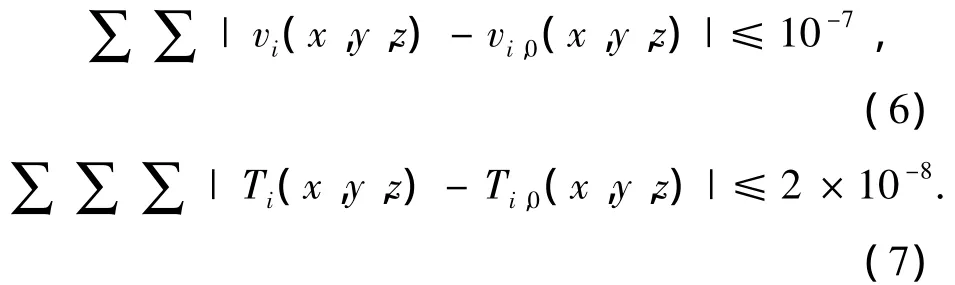
1.4 数值计算有效性检验

文献［3］中提供的等截面矩形微通道压降计算公式为

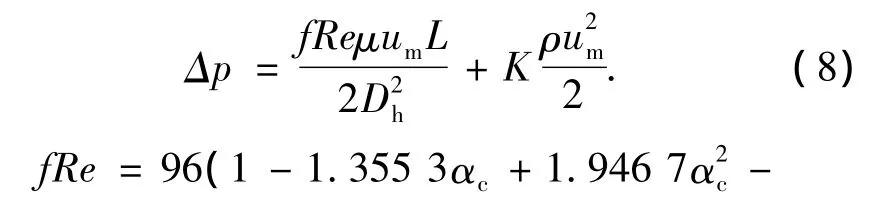
式中:αc为微通道宽高比;um为等截面矩形微通道流体流速平均值，m/s.

等截面矩形微通道压降计算结果与式(8)计算结果比较见图3，通过比较可知两者吻合的非常好，最大误差为2.8%，证明了等截面矩形微通道数值计算的有效性.扇形凹穴型微通道采用相同的处理方法，从而证明了扇形凹穴型微通道数值计算的有效性.

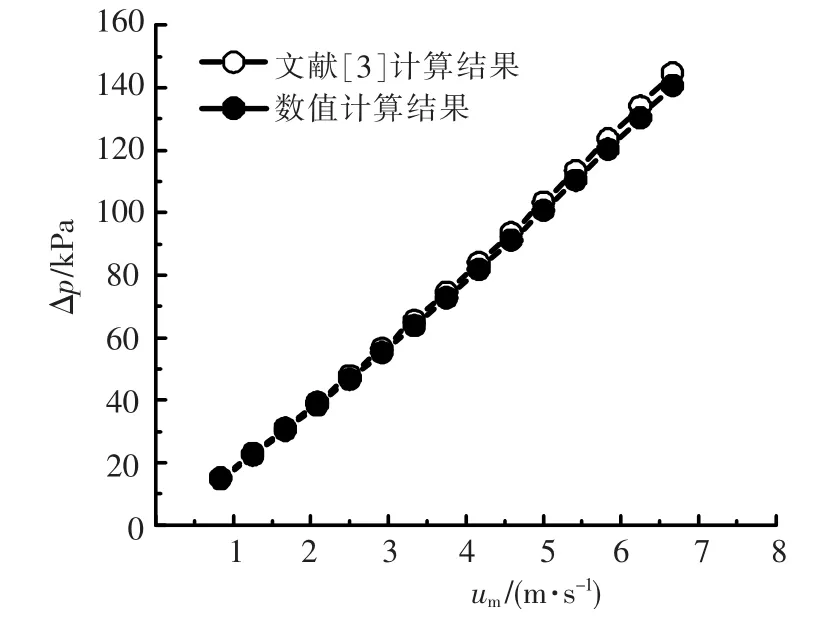
图3 数值计算压降值与文献［3］计算压降值比较

2 结果与讨论

扇形凹穴型微通道在结构上与波纹管具有很大的相似性.文献［15］将波纹管的摩擦阻力特性归结于层流滞止区与喷射节流效应的相互作用，将强化传热特性归结于边界层的破坏和喷射节流效应.

2.1 流动特性

图4给出了不同流量下微通道内中心线上流体的压力随流动方向的变化关系，实线代表扇形凹穴型微通道，虚线代表等截面矩形微通道.由于扇形凹穴型微通道热沉相邻两微通道略有差异取相邻两微通道中心线上流体压力的平均值.从图中可以看出扇形凹穴型微通道内流体压力沿流动方向锯齿型下降.这主要是由于扇形凹穴型微通道内流体流动分为等直径流速型和弧形流速型，流体沿流动方向在扇形凹穴处速度降低、静压增大;等直径通道处速度增加，静压减小，使流速和压力总是处于规律性的扰动状态.

图5给出了不同底面热流密度条件下微通道内流体摩擦阻力系数f随Re的变化关系.文献［16］中摩擦阻力系数f的计算公式为

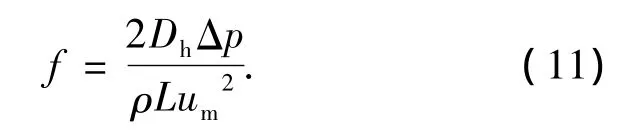
Re的计算公式为

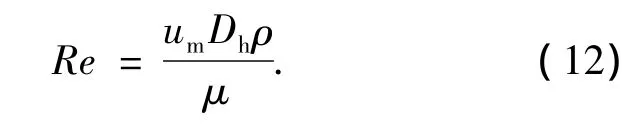
式(11)和式(12)中的等截面矩形微通道um值取流体流速平均值，扇形凹穴型微通道um值取等直径段处流体流速平均值.动力黏度μ取体平均值，Δp为通道进出口压差.从图中可以看出随Re增加扇形凹穴型微通道摩擦系数逐渐大于等截面矩形微通道.一方面小Re条件下流体在扇形凹穴处出现层流滞止区，该作用使压降减小;另一方面在较大Re条件下在扇形凹穴进出口处发生喷射节流效应，该作用使压降增大.从图中还可以看出，对于不同的底面热流密度，扇形凹穴型微通道中流体的f-Re曲线几乎重合，而等截面矩形微通道却有差异.这主要是随热流密度增大，一方面流体的动力黏度降低，减小了摩擦阻力系数;另一方面扇形凹穴喷射和节流效应增强，增大了摩擦阻力系数.两者相互作用使扇形凹穴型微通道中流体的f-Re曲线几乎重合.

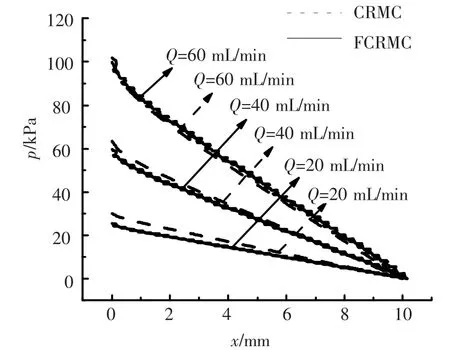
图4 不同流量下通道内流体压力沿流动方向的变化

图5 f与Re的关系

2.2 传热特性

图6给出了在流体进口温度T=289 K，微通道热沉体积流量为Q=20 mL/min，热沉底面热流密度q=670.789 kW/m2时，微通道热沉底面温度Two、流体与固体接触壁表面温度Twi和流体温度Tf沿流动方向的变化关系.等截面矩形微通道流体温度Tf取微通道中心线上的数值，扇形凹穴型微通道热沉取相邻两微通道中心线上流体温度的平均值.从图中可以明显的看出，扇形凹穴型微通道热沉温度与通道内流体的温度差远小于等截面矩形微通道热沉，可以达到30%.这一方面是由于扇形凹穴的喷射节流效应使热边界层不断的中断和再发展，换热得到强化;另一方面扇形凹穴的存在增大了换热面积，强化了冷却效果.流体沿流动方向依次交替地收缩和扩张，在扩张段中产生强烈的漩涡被流体带入收缩段时得到了有效的利用，且收缩段内流速增高会使流体层流底层变薄，这些都有利于增强传热.

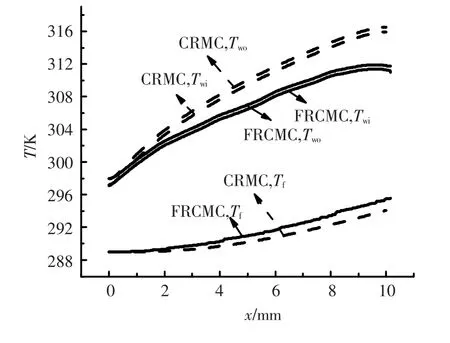
图6 热沉底面温度、固液接触壁面温度、流体温度随流动方向的变化

图7给出了不同底面热流密度条件下微通道内流体平均Nu随Re的变化关系.文献［16］中平均Nu的计算公为

式中:Φ为所取基本单元底面的加热功率;Ach为单个通道固液接触面积，为了便于比较，两微通道热沉均取Ach=(a+2b)L;λf为流体导热率;ΔT取微通道内底面温度与流体进出口温度平均值的差值.

从图8可以看出在小Re条件下扇形凹穴型微通道热沉的换热效果不如等截面矩形微通道热沉;而在较大Re条件下其换热效果远大于等截面矩形微通道，且随Re的增大强化传热效果越好.这主要是由于小Re条件下，扇形凹穴内层流滞止区大大影响了传热效果;较大Re条件下，扇形凹穴的喷射节流效应增强，强化传热效果显著.从图中还可以看出，随着底面热流密度的增加，等截面矩形微通道Nu-Re曲线变化不明显，而扇形凹穴型微通道的Nu-Re曲线变化明显.同时也说明扇形凹穴扇形凹穴的喷射和节流效应强化了传热效果.

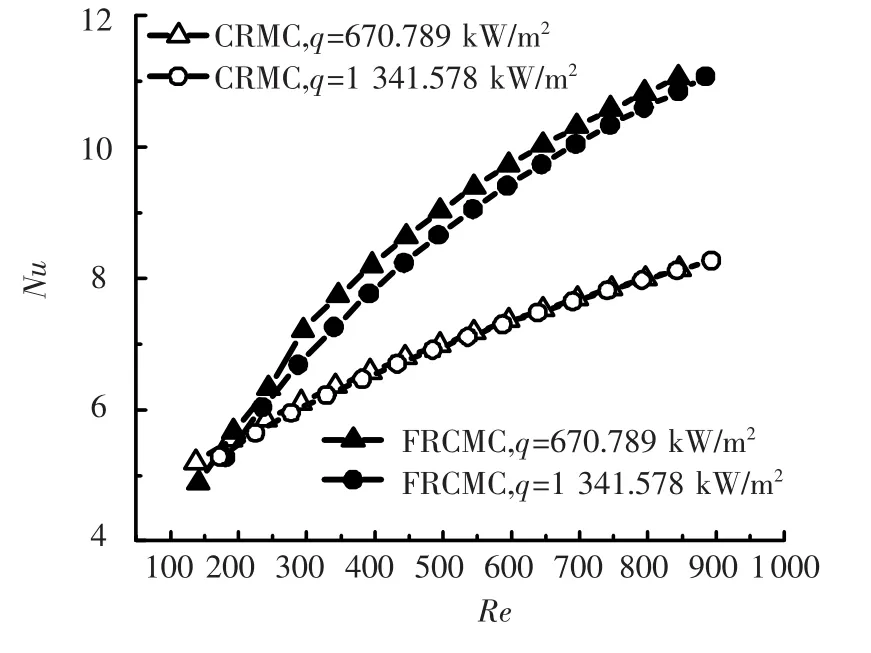
图7 Nu与Re的关系

在实际的热沉设计过程中，压降随热阻的变化关系是评价一个热沉换热效果好坏的重要标准，它直接反映整个热沉系统运行的经济性.虽然不同的文献对热沉热阻的定义不同，然而大多数的文献中定义热沉热阻为热沉底面最高温度与流体进口温度差值除以热沉底面的加热功率所得的比值.其公式为

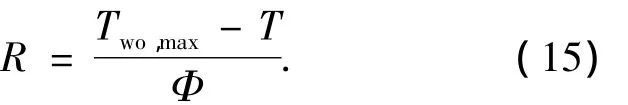
式中:Two，max为热沉底面最高温度;T为流体进口温度;Φ为热沉底面加热功率.

扇形凹穴型微通道和等截面矩形微通道热沉压降随热阻的变化关系如图8所示.

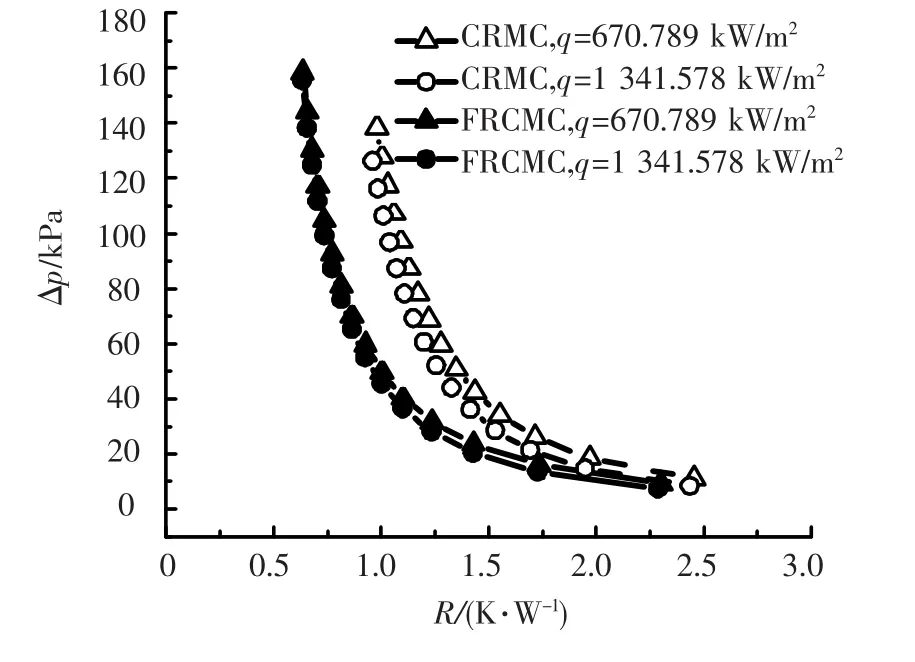
图8 压降随热阻的变化关系

从图中可以看出在相同的压降条件下，扇形凹穴型微通道热沉的热阻远小于等截面矩形微通道热沉.说明扇形凹穴型微通道热沉的换热效果及整个热沉运行的经济性远好于等截面矩形微通道热沉.从图中还可以看出，微通道流体压降随热阻增加急剧减小，但当压降降低到一定水平后，压降降低速度放缓.同时说明在一定范围内，随压降增加，热阻变化不大，因此不能通过一味地增加流体体积流量以增加压降来提高微通道热沉的换热性能.

3 结论

1)扇形凹穴型微通道内流体压力沿流动方向锯齿型下降.扇形凹穴破坏流动边界层使流体产生扰流，有利于传热，流动阻力却增加不多.

2)扇形凹穴的喷射节流效应和增大换热面积作用使扇形凹穴型微通道热沉的换热效果远好于等截面矩形微通道热沉.不能通过一味地增加流体体积流量以增加压降来提高微通道热沉的换热性能.

3)扇形凹穴型微通道热沉传热机理可归结为边界层的破坏、喷射节流效应及层流滞止区的相互作用.

［1］TUCKERMAN D B，PEASE R F.High performance heat sink for VLSI［J］.IEEE Electron Dev Lett，1981，2:126-129.

［2］CELATA G P，CUMO M.Experimental investigation of hydraulic and single phase heat transfer in 0.130mm capillary tube［J］.Microscale Thermophys，2002，6: 85-97.

［3］STEINKE M E，KANDLIKAR S G.Single-phase liquid friction factors in microchannels［J］.International Journal of Thermal Sciences，2006，45:1073-1083.

［4］XIE X L，LIU Z J.Numerical study of laminar heat transfer and pressure drop characteristics in a watercooled minichannel heat sink［J］.Applied Thermal Engineering，2009，29:64-74.

［5］HARPOLE G，ENINGER J E.Microchannel heat exchanger optimization［J］.Proceedings IEEE Semiconductor Thermal，1991，2:59-63.

［6］KNIGHE R W，HALL D J.Heat sink optimization with application to microchannels［J］.IEEE Transactions on Components，Hybrids，and Manufacturing Technology，1992，15(5):832-842.

［7］KANDLOKAR S G，UPADHYE H R.Extending the heat flux limit with enhanced microchannels in direct single-phase cooling of computer chips［J］.IEEE Semiconductor Thermal，2005，21:15-17.

［8］KANDLIKAR S G，JOSHI S.Effect of surface roughness on heat transfer and fluid flow characteristics at low Reynolds numbers in small diameter tubes［J］.Heat Transfer Engineering，2003，24(3):4-16.

［9］GIULIO C，PAOLA D.Three-dimensional roughness effect on microchannel heat transfer and pressure drop［J］.International Journal of Heat and Mass Transfer，2007，50:5249-5259.

［10］PENG X F，PETERSON G P.Convective heat transfer and flow friction for water flow in micro-channel structures［J］.Int J Heat and Mass Transfer，1996，39: 2599-2608.

［11］HEINZ H，SHRIPAD P.Variable property effects in single-phase incompressible flows through microchannels［J］.International Journal of Thermal Sciences，2006，45:977-981.

［12］LI Z G，HUAI X L.Effects of thermal property variations on the liquid flow and heat transfer in microchannel heat sinks［J］.Applied Thermal Engineering，2007，27:2803-2814.

［13］GIUDICE S D，NONINO C.Effects of viscous dissipation and temperature dependent viscosity in thermally and simultaneously developing laminar flows in microchannels［J］.International Journal of Heat and Fluid Flow，2007，28:15-27.

［14］杨世铭，陶文铨.传热学［M］.3版.北京:高等教育出版社，1998.

［15］崔海亭，彭培英.强化传热新技术及其应用［M］.北京:化学工业出版社，2005.

［16］SATISH G K，MICHAEL R K.Heat transfer and fluid flow in minichannels and microchannel［M］.Oxford: Elsevier Ltd，2006.