交流电场作用下具有导电率梯度的两相微流体驱动

姜洪原，任玉坤，A.Ramos

(1.哈尔滨工业大学机械设计系，150001哈尔滨，jhy-hit@sina.com;2.浙江大学流体传动及控制国家重点实验室，310027杭州;3.西班牙塞维利亚大学电子电磁学院，41012塞维利亚)

微系统中流体动力学研究是MEMS技术和芯片实验室(Lab-on-chip)发展过程中的一项核心内容，被越来越广泛地关注［1-2］.为此，衍生出多种精确控制微小体积流体的微机械结构来进行流体的相关操控研究［3］;但是由于这些机械结构均具有可移动部件，使得加工和实验操作过程变得较为复杂，大大降低了流体控制的可靠性和稳定性，为此，人们试图寻求一种无移动部件的微流体控制结构.

基于交流电场机制的微流体操控是实现这一无移动部件要求的核心技术，具有很多优势，如低能耗、无电解产生以及易与其他流体器件集成等.这一操作过程是通过对沉积在微通道中的微电极施加电信号，进而产生电场力对流体进行驱动与控制的.由交流电场产生的力不仅作用在流体上而且也会对双电层产生较大的影响［4］.例如，利用交流电渗技术对流体进行驱动时只需要在电极上施加极低的电压(＜2 V)就可在固-液交界面处获得较大的力，进而拖动整个流体的流动.由于所需电压较低，因此耗能少，无电解产生，是实现流体驱动的一种新型方法［5-9］.

芯片实验室研究中，将多种功能集成到一块几平方厘米的芯片上进行相关分析是一项具有重要前景的研究工作，而不同流体的流动路径控制是连通各个功能的核心，具有重要的研究价值［10］.不同种流体之间具有的物理性质差异，会形成一定的导电率梯度，耦合以电场的作用，会在流体内部产生力的作用，这一特点在多相流体的路径控制、单相流体的微泵式驱动中均具有重要意义［11-12］.

基于上述交流电场机制进行流体驱动的优点，笔者利用交流电场对微通道中具有导电率梯度的两相同向流体进行了操控研究.具体实验模型见图1，指型交叉电极沉积在微通道的底部(具体电极尺寸在仿真部分交代)，两相同向流体注入微通道中，由于在微尺寸范围内研究问题，因此雷诺数很低，为层流流动.然后对电极施加相位差180°的交流电信号，观察实验现象.实验中选择2种不同导电率KCl溶液作为待操作流体，令其导电率分别为σ1(左侧)和σ2(右侧)，且σ1＜σ2.为便于在显微镜下观察分析，对高导电率流体进行荧光染色，如图1所示两相流体呈现不同颜色，右侧流体为染色后的流体.

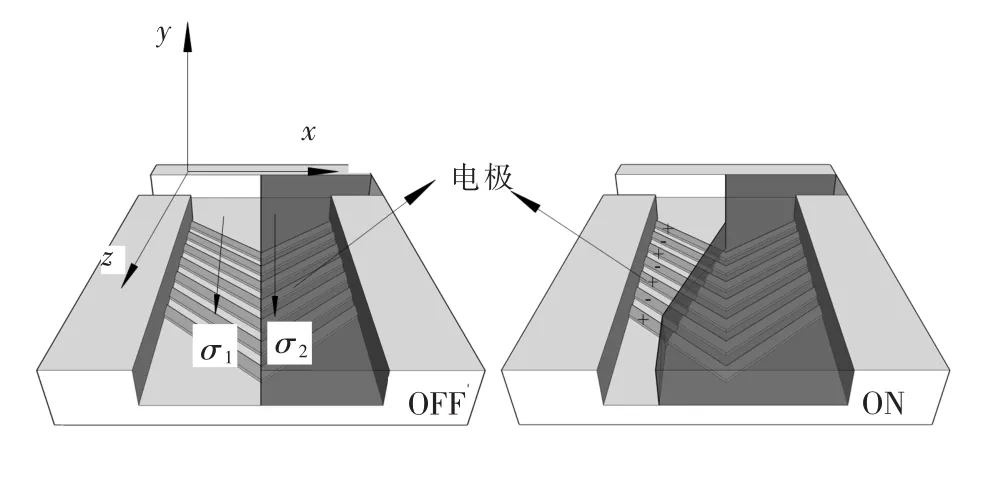
图1 两相流体控制实验三维模型

实验结果见图2.对沉积在微通道底部的电极施加电信号时，导电率较高的溶液将发生倾斜，并且占据整个通道，将低导电率液体挤出通道，撤掉电信号后，流体恢复初始状态.这一实验研究将对生物微系统或者医药医学微研究领域的低能高精度分选以及微纳粒子分离等前沿技术产生重要影响.

本文在实验研究基础上，对具有导电率梯度的两相流体驱动进行深入研究.首先建立二维理论模型，分析其机理;然后，对实验系统进行了数值分析，通过电荷守恒方程，对流扩散方程以及Navier-Stokes方程对实验过程进行了描述;最后，对理论模型进行仿真研究，获得两相流体操控实验的瞬时以及稳态仿真结果，并着重分析了频率对实验的影响，理论解释了两相流体的驱动过程.为展开对两相以及多相流体的控制研究提供了理论依据和仿真基础.

图2 交流电场驱动两相流体实验结果

1 机理分析

为了便于分析机理以及获得合理实验参数，建立如图3所示二维物理模型.实验用微通道中，电极厚度以及宽度远小于其长度，因此z向可认为无限远，在x-y平面进行研究.将导电率不同的两相流体(σ1和σ2)注入通道，图中直线为两相流体之间的交界面.每相邻两个电极施加电压幅值差为2V0的电信号，也就是每个电极施加电压为Vi(t)=(-1)iV0cos(ωt)，其中i=1，2， 3…，ω为电信号的角频率.为了更充分地分析导电率梯度与电场的相互作用，假设左右两边界的导电率为固定值，进而产生固定的导电率梯度［13］.

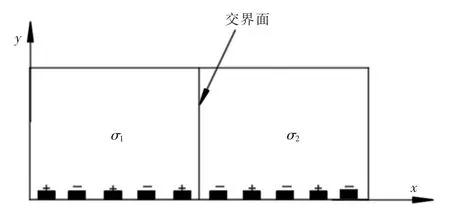
图3 二维分析模型

流体产生流动是力作用的结果，由于实验中施加电信号频率足够大可以忽略双电层的影响，所以作用于流体上的体力为［14］

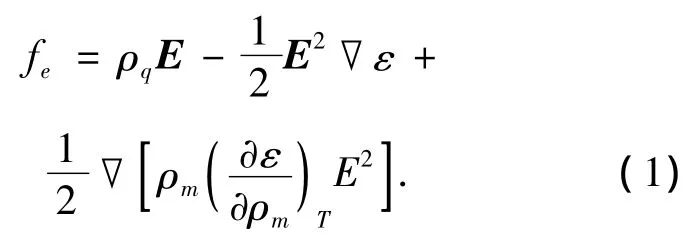
式中:ρq、ρm、ε、T、E分别代表电荷密度、质量密度、电介质介电常数、温度和电场.式(1)右边第一项和第二项分别为库仑力和电介质力，最后一项为在不可压缩流体中可忽略的电致伸缩力.由于本实验采用的2种流体均为KCl溶液，因此具有相同的介电常数，介电常数的梯度为0，右边第二项忽略.这样在两相流体交界面处的力将只有作用于净电荷上的库仑力.

为了对该系统进行定性分析，首先考虑一对电极，如图4所示.在该模型中选择一矩形区域(abdc)进行分析，oo'为两种流体的交界面.

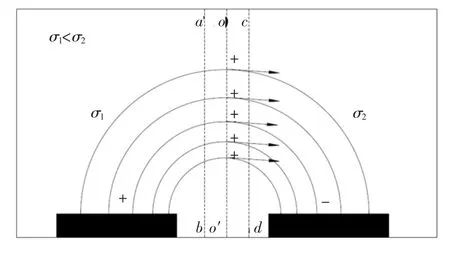
图4 具有一对电极的机理分析模型

两相流体的交界面处，法向电流满足电流连续方程

式中n，J1，J2分别为方向单位矢量，左侧电流密度和右侧电流密度.根据欧姆定律可知电流密度等于导电率与电场强度的乘积，即J=σE，令左右两侧电场强度分别为E1和E2，于是方程(2)可整理为

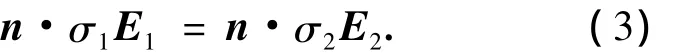
由高斯定理可知，在两相流体交界面处的净电荷为

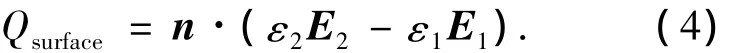
式中ε1，ε2分别为两种流体的介电常数.由于实验用两相流体均为KCl溶液，因此具有相同的介电常数，即ε=ε1=ε2，联立式(2)～(4)得

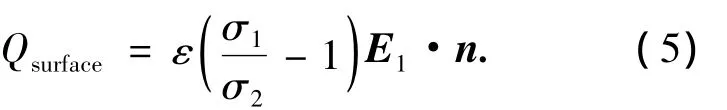
由式(5)可知，当σ1＜σ2时，Qsurface＜0，由于电场方向为自左向右，因此两相流体交界面处的库仑力向左;反之如果σ1＞σ2，则交界面处的库仑力向右;实验中所用流体导电率为σ1＜σ2，所以当施加电信号时，流体交界面处受力向左，使得右侧高导电率流体迅速左移，与实验现象完全一致.

2 数值分析

对实验用模型(图3)进行数值仿真研究.实验过程中，影响实验现象的主要因素为两相流体的导电率梯度，施加交流信号产生的交流电场，以及流体的流动等，为了使仿真更接近实验过程，利用电荷守恒方程、对流扩散方程以及 Navier-Stokes方程对实验进行描述，并对其进行耦合研究［15-17］.

电荷守恒方程描述了两相流体交界面处的电荷规律，即

式中φ为电势.电荷守恒方程满足的边界条件为电极上施加电压信号，其余边界法向电流为0.

假设整个系统呈电中性，两相流体的交界面处满足对流扩散方程，即

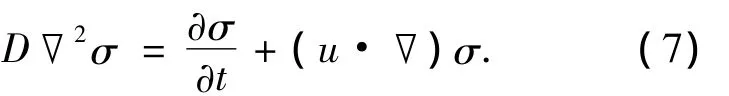
式中:D为扩散系数;u为流体流动速度.对流扩散方程边界条件为左右两侧固定导电率分别为σ1和σ2，其余边界法向变化为0.

微系统中，雷诺数Re=ρmud/η，通常远小于1，本实验中，ρm和η分别为质量密度和流体黏度，u为特征速度(约为1 mm/s)，d为特征长度(约为10 μm)，计算的雷诺数约为10-3［10］.因此流体的流动可以用Navier-Stokes方程进行表示，即

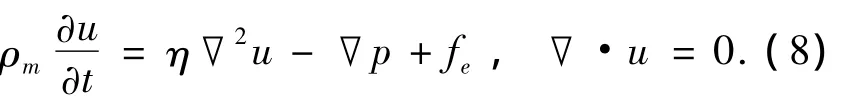
式中:p为压力;fe为作用于流体的平均时间库仑力.由于电极上施加电信号周期远小于系统的特征振动时间，因此可以考虑作用力为平均时间库仑力.考虑泊松方程有

联立式(6)和式(9)可得交界面处净电荷密度的表达式为

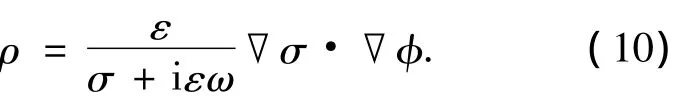
于是平均时间库仑力为

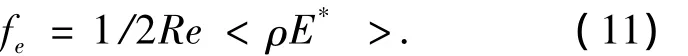
式中E*为电场强度的复数相量.因此 Navier-Stokes方程的边界条件为对于各边界速度均为0.

综上所述，实验中对于两相流体的操控过程是电荷守恒方程、对流扩散方程以及 Navier-Stokes方程共同作用的结果，因此仿真过程中应对上述3个基本方程进行耦合求解.

3 仿真结果分析

利用COMSOL Multiphysics软件进行仿真分析，见图3.仿真区域宽度250 μm，高度120 μm，形成一个封闭区域，底部沉积10个电极，由于电极厚度仅为100 nm，可忽略，电极宽度为15 μm，极间距为10 μm，相邻电极施加电压分别为±V0，即电势差为2V0.

3.1 瞬态仿真分析

瞬态仿真研究中，分别设置导电率为σ2= 0.02 s/m，σ1=0.01 s/m，也就是仿真区域中右侧导电率为左侧导电率的2倍.简单起见，瞬态仿真中，令角频率ω≪σ/ε(f≪106Hz)，忽略频率影响，施加在电极上的电压幅值为±1 V，初始状态如图5所示，左右两侧为两相同向流动的不同导电率的流体.

图5 未施加电信号的初始状态

图6为导电率随时间的变化曲线，仿真时间分别为0.01、0.1、1和3 s，对比图6(c)与图6 (d)可知，流体驱动过程非常迅速，时间超过1 s以后，导电率基本处于稳态，无明显变化.从图6 (a)到图6(d)，不难看出，两相流体交界面发生倾斜，具有高导电率的流体将占据整个通道，这与实验结果有很好的一致性，说明仿真的正确性与可行性.

图6 瞬态仿真结果

3.2 稳态仿真分析

瞬态仿真中，角频率ω≪σ/ε(f≪106Hz)可忽略，而在稳态仿真中，为了详细分析频率对于实验的影响，固定其他参数不变，调整仿真频率范围100～109Hz，如图7所示为分别选择频率为100、104、106、107和109Hz时的稳态仿真结果.

图7 稳态仿真导电率随频率变化的结果

频率＜106Hz时，稳态状态变化不大，而当频率＞106Hz时，可见两相流体交界面倾斜程度迅速降低，当频率接近109Hz时，交界面基本无变化，即此时库仑力近似为0.考虑式(10)，由两相流体交界面处的净电荷表达式可知，当ω≪σ/ε时，角频率对平均时间库仑力的影响可忽略，而在仿真过程中，随着频率的不断升高，其对净电荷密度的影响逐渐增大，进而影响平均时间库仑力;当ω≫σ/ε时，净电荷密度逐渐趋于0，因此平均时间库仑力亦接近于0，从而使得两相流体交界面无明显倾斜变化.因此实验过程中，适当调节频率，可有效提高两相流体的控制效率.

4 结语

通过对微通道内交叉指型微电极施加交流电信号，进行了具有导电率梯度的两相流体控制实验.结果表明:施加电信号时，具有高导电率的流体会迅速将低导电率流体挤出微通道，并且占据整个通道;撤掉电信号时，两相流体恢复初始状态.以两相流体交界面处导电率梯度和电场综合作用产生的净电荷计算为基础，进行了流体所受库仑力的推导，解释了产生实验现象的原因.耦合电荷守恒方程、对流扩散方程以及Navier-Stokes方程进行仿真研究，获得了与实验现象一致的仿真结果.分析了导电率随时间变化的规律，着重分析了稳态时，频率对于实验的影响，为后续微系统中多相流体驱动与分离等方面的研究奠定了理论基础.

［1］ STONE H，STROOCK A，AJDARI A.Engineering flows in small devices:microfluidics towards a labon-a-chip［J］.Annu Rev Fluid Mech，2004，36: 381-411.

［2］ HARDT S，SCHÖNFELD F.Microfluidic technologies for miniaturized analysis systems［M］.New York: Springer-Verlag，2007:59-60.

［3］ RAMOS A，MORGAN H，GREEN N G，et al.AC electrokinetics:a review of forces in microelectrode structures［J］.J Phys D:Appl Phys，1998，31: 2338-2353.

［4］ 刘国君，程光明，杨志刚.一种压电式精密输液微泵的试验研究［J］.光学精密工程，2006，14(4):612-616.

［5］ KOCH M，EVANS A，BRUNNSCHEWILER A.Microfluidic technology and applications［M］.Herts:Research Studies Ltd.，2000:25-50.

［6］ STUDER V，PEPIN A，CHEN Y，et al.An integrated AC electrokinetic pump in a microfluidic loop for fast and tunable flow control［J］.The Analyst，2004，29: 944-949.

［7］ CAHILL B P，HEYDERMAN L J，GOBRECHT J，et al.Flow reversal at low voltage and low frequency in a microfabricated ac electrokinetic pump［J］.Physical Review E，2007，76:036305-036314.

［8］ RAMOS A，Morgan H，GREEN N G，et al.AC electric-field-induced fluid flow in microelectrodes［J］.J Colloid and Interface Science，1999，217:420-422.

［9］ RAMOS A，GONZÁNCHEZ A.A linear analysis of the effect of Faradaic currents on traveling-wave electroosmosis［J］.J Colloid Interface Sci，2007，309:323-331.

［10］ JHUNJHUNWALA M.Multiphase flow and control of fluid path in microsystems［D］.Massachusetts:Massachusetts Institute of Technology，2003.

［11］ CHEN Lingxin，LEE S.Continuous dynamic flow micropumps for microfluid manipulation［J］.Micromech Microeng，2008，18:013001-013022.

［12］ LASER D，SANTIAGO J.A review of micropumps［J］.Micromech Microeng，2004，14:35-64.

［13］ JIANG Hongyuan，REN Yukun，AO Hongrui.Electrohydromechanical analysis based on conductivity gradient in microchannel［J］.chin Phys， 2008，17 (12):4541-4547.

［14］ STRATTON J A.Electromagnetic theory［M］.New York:McGraw-Hill，1941:508-510.

［15］ CASTELLANOS A，RAMOS A，GONZALEZ A，et al.Electrohydrodynamics and dielectrophoresis in microsystems:scaling laws［J］.J Phys D:Appl Phys，2003，36:2584-2597

［16］ NEWMAN J S，THOMAS-ALYEA K E.Electrochemical systems［M］.Hoboken，NJ:Wiley-Interscience，2004:517-562.

［17］ CHEN CH，LIN H，LELE S K，et al.Convective and absolute electrokinetic instability with conductivity gradients［J］.J Fluid Mech，2005， 524:263-303