三塔悬索桥刚性中塔的鞍缆防滑技术

李 扬，肖汝诚，周云岗

(同济大学桥梁工程系，200092上海，033669@gmail.com)

悬索桥因其卓著的跨越能力而在大跨桥梁中备受青睐.随着跨度的增大，双塔悬索桥需要建造庞大的锚碇，从而降低了经济性能.在我国长江中下游地带，土质松软、覆盖层厚、基岩埋深大，锚碇费用过高已成为限制悬索桥发展的瓶颈［1］.三塔悬索桥相比大单跨悬索桥可显著减小主缆拉力和锚碇规模.因此当跨中水深不大时，三塔悬索桥将成为有力的竞争方案.

三塔悬索桥的中塔结构形式是设计的关键问题之一［2-3］.中塔结构可分为柔性和刚性两类.当车辆活载在一跨满布而在另一跨空载时，采用柔性中塔会使塔顶位移过大，从而导致悬索桥整体刚度不足［4］.为此中塔往往设计成刚性塔［5］.然而刚性中塔在上述偏载工况下将承受极大的主缆不平衡水平力，中塔塔顶处主缆和索鞍的抗滑安全系数成为控制设计的一个重要指标［6］.为了提高这一系数，传统的方法有增加缆、鞍材料的摩阻系数、增大索鞍切向尺寸、竖向加压等措施［7-9］，这些都属于提高抗滑摩擦力的“被动措施”，对材料性能、塔顶尺寸等要求较为严格，有时难以应用.

本文从直接减小索鞍两侧主缆不平衡力的观点出发，提出了5个鞍缆防滑的“主动措施”，并研究了它们的有效性.

1 问题的提出

泰州长江大桥是一座三塔两跨悬索桥，跨径组合为390 m+1080 m+1080 m+390 m，矢跨比为1/9，标准吊杆间距为16 m.上下游主缆截面积共为0.595 2 m2.主梁为钢箱梁，截面积为1.514 4 m2，抗弯惯性矩为2.92 m4.当采用A形刚性中塔时，计算模型见图1.

图1 三塔悬索桥的计算模型(m)

令计算得到的索鞍松侧和紧侧主缆拉力分别为T1和T2，主缆与索鞍材料的摩阻系数为μ，则鞍、缆抗滑安全系数K为［10］

式中θ为索鞍两侧主缆切点间的圆心角，它与变形后的主缆在塔顶的倾角有关.可以证明采用刚性中塔时，活载引起的主缆倾角变化十分有限.以泰州长江大桥为例，活载在一跨满布而在另一跨空载时，主缆在中塔塔顶的倾角仅比成桥状态下的倾角增大0.57%.因此θ值可按成桥线形计算，而忽略活载对主缆线形的影响.如图2所示，当中塔塔顶鞍座关于中塔轴线对称时，根据相似三角形的关系知T2/T1=H2/H1，因此K值还可直接用两侧水平拉力H1和H2代入求解.考虑最不利荷载工况时，H1和H2分别表示在一跨满布活载(其中集中活载作用于该跨跨中)而在另一跨空载时的松、紧两侧水平拉力.

图2 索鞍受力示意

泰州长江大桥的索鞍圆心角为θ=0.84 rad，摩阻系数μ通常取0.15，但一些抗滑试验［7］证明泰州大桥可以采用0.2，本文同时考虑这2种情况.在前述最不利活载工况下，用有限元方法计算得到索鞍两侧主缆的拉力值，利用式(1)可以算出当 μ=0.15时抗滑安全系数 K0.15=1.088，μ=0.2时K0.2=1.451，均小于规范［11］推荐值［K］=2.0.

可见，采用刚性中塔时，泰州长江大桥中塔处的鞍、缆之间有发生滑动的危险，因此有必要采取适当的措施提高鞍缆的防滑性能.

2 索鞍与主缆的防滑方案

2.1 中央扣方案

按图3所示的方式在各跨跨中设置中央扣，上下游两侧弹性索总面积为0.012 6 m2.通过中央扣加强主梁与主缆间的联系，以改善活载作用下的主缆受力.

图3 中央扣布置形式

2.2 矢跨比方案

由式(1)可知，K值与主缆拉力以及主缆与索鞍切点间的圆心角θ有关.通过改变主缆的矢跨比，可以同时影响T1、T2和θ的取值，从而改变鞍缆抗滑安全系数K.

2.3 扣索方案

成桥后在塔根和主缆之间设置扣索，如图4所示.该方案的出发点是希望在活载作用下通过扣索的受力将主缆水平拉力由H2减小至H'2，以提高抗滑安全系数K.

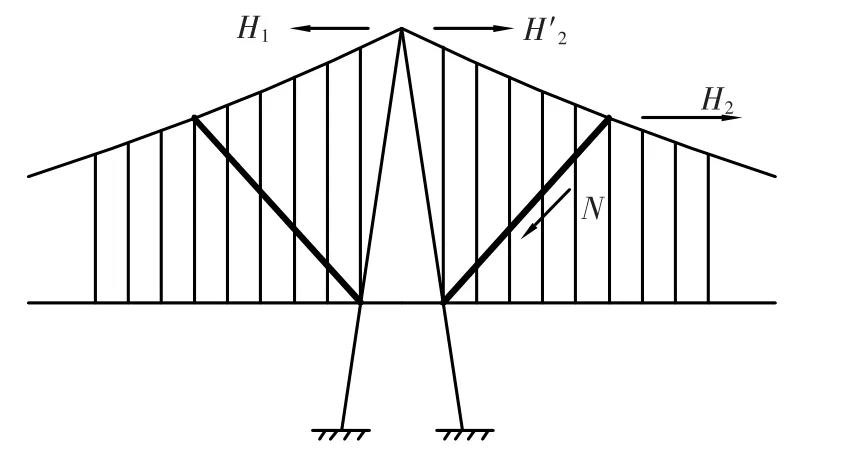
图4 在塔根和主缆之间增设扣索

2.4 钢结构方案

成桥后在塔顶和主缆之间设置受力构件以减小索鞍处的主缆受力，如图5所示.由于该构件尺寸较小，可以设计成钢结构的形式，不仅可以受拉受压，同时能承受弯矩.

2.5 辅助拉索方案

在索鞍两侧附近的主缆上附加一部分拉索，以协助主缆受力，这些辅助拉索直接锚固在索鞍上，如图6所示.此时主缆和辅助拉索的拉力将直接按照轴向刚度分配，受力明确.

图5 在塔顶和主缆之间设置钢结构

图6 辅助拉索方案

3 防滑方案的效果分析

3.1 中央扣方案

通过计算发现，在最不利活载工况下，中央扣对索鞍两侧主缆的拉力影响不大，此时鞍缆抗滑安全系数变为K0.15=1.085，K0.2=1.447.因此中央扣通常虽然可以提高结构刚度［12］，但对于改善鞍座处的抗滑性能没有贡献.

3.2 矢跨比方案

当中塔抗推刚度很大时，式(1)中的H1可认为是恒载作用下的水平拉力，H2则代表恒、载共同作用下的水平拉力.在没有增设其他附加受力部件(如上文提到的扣索等)的情况下，H1和H2容易通过解析法求得.记gc和gd分别表示主缆和主梁的恒载集度，f和l分别表示矢高和跨径，则H1可按下式估算［13］:

图7 集中力作用下的中跨主缆模型

此外，若取主缆在跨中的最低点为坐标原点，x轴向右，y轴向上，则主缆与索鞍间切点的圆心角为

将式(2)～(4)代入式(1)可得鞍缆抗滑安全系数估算公式

由式(5)可以看出矢跨比并不能改变索鞍紧、松两侧主缆拉力的比值T2/T1，但却能改变主缆与索鞍间切点的圆心角θ.随着矢跨比的增加，鞍缆抗滑性能也将得到改善.图8所示为有限元计算结果，可以看出f/l=1/8时的抗滑安全系数比f/l=1/12时提高了27.0%，验证了上述结论.

3.3 扣索方案

在塔根与主缆间设置扣索，是为了利用扣索的张拉力减小主缆的不平衡水平力.但通过有限元进行非线性分析发现，活载作用下由于桥塔刚度很大，塔顶位移很小，同时主缆下挠，使得扣索两端距离不仅没有伸长反而缩短，如图9所示.如果扣索不进行初张拉，则由于不能承受压力而退出工作;如果扣索进行初张拉，则扣索的卸载相当于反向施加了压力，使得H'2＞H2，反而加剧了滑动的趋势.此外，扣索对主缆与索鞍间切点的圆心角θ影响甚小，即使令扣索与主缆截面和张拉力相等，θ也仅从0.84 rad变为0.88 rad，只增大了4.8%.因此认为增设扣索效果甚微.

3.4 钢结构方案

如图5所示，钢结构构件有3个关键的设计参数，即构件与主缆的夹角α、构件自身的截面积A和抗弯惯矩I(均为上下游两侧的总和).先令A=1.0 m2，I=1.0 m4，改变α的取值，通过有限元分析可以得到抗滑安全系数K值与α的关系如图10所示.可以看出当α在60°左右时效率最高.

图9 扣索的变形

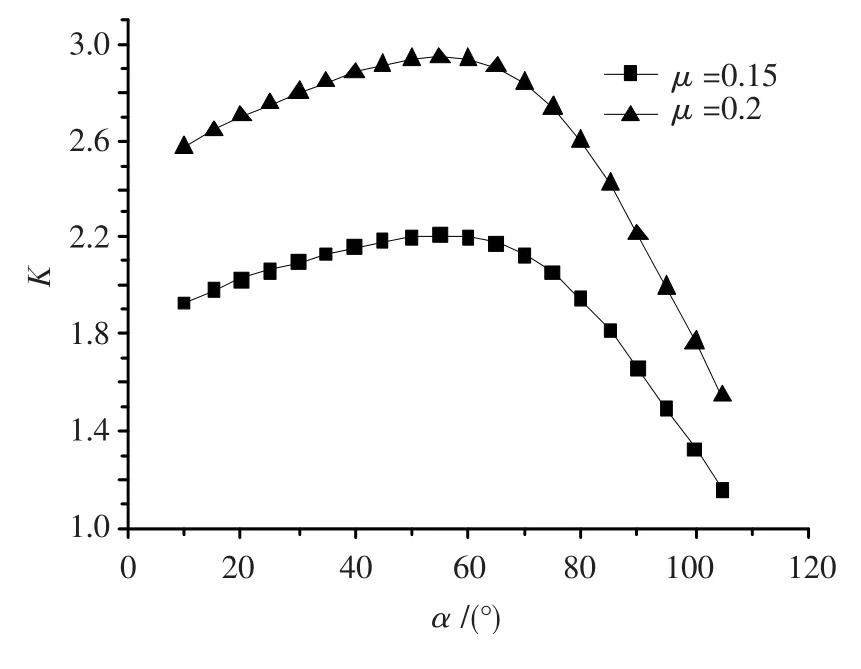
图10 K值与α的关系

令α=60°，改变A、I的取值，通过有限元分析可以得到K值与A、I的关系如图11所示.从图11可以得到如下结论:①当抗弯惯矩I=0时，无论截面积A取多大的值，都不会提高抗滑安全系数.这就是说，此处的钢结构构件必须同时具有轴向刚度和抗弯刚度，而不能设计成仅受轴力的二力杆.②图中以曲线2.0为界限，其右上侧区域的K值均大于2.0，为该方案的可行域，随着摩阻系数的增大，可行域的范围也变大.③由于截面积A直接表征了材料用量，因此A应该取较小值，同时综合考虑抗弯刚度的取值，图中M点对应的取值较为经济.泰州大桥的摩阻系数取μ=0.2，此时M点对应的A=0.2 m2，I=0.5 m4(均为上下游两侧的总和)，即每支构件的面积和抗弯惯矩仅为A1=0.1 m2，I1=0.25 m4.从构造上考虑，该构件设计成桁架式结构较为适宜.

3.5 辅助拉索方案

设主缆面积为A0，原来松紧两侧的主缆拉力分别为T1和T2，鞍缆抗滑安全系数为K0，小于规范要求的最小值［K］.为提高抗滑性能，需采用的辅助索面积最小为ΔA，此时它承受的张拉力为ΔT，主缆拉力则减小为T'2.由式(1)易知

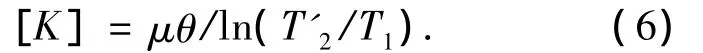
活载作用下主缆和辅助拉索之间的拉力按照轴向刚度分配，因此有

联立式(6)和式(7)，可得

式中［k］=2.0，A0和θ已知，T1、T2则在初始模型计算时均可得到.因此通过上式可得到所需辅助拉索的最小面积ΔA与摩阻系数μ的关系，如图12所示.

图11 K值与A、I的关系

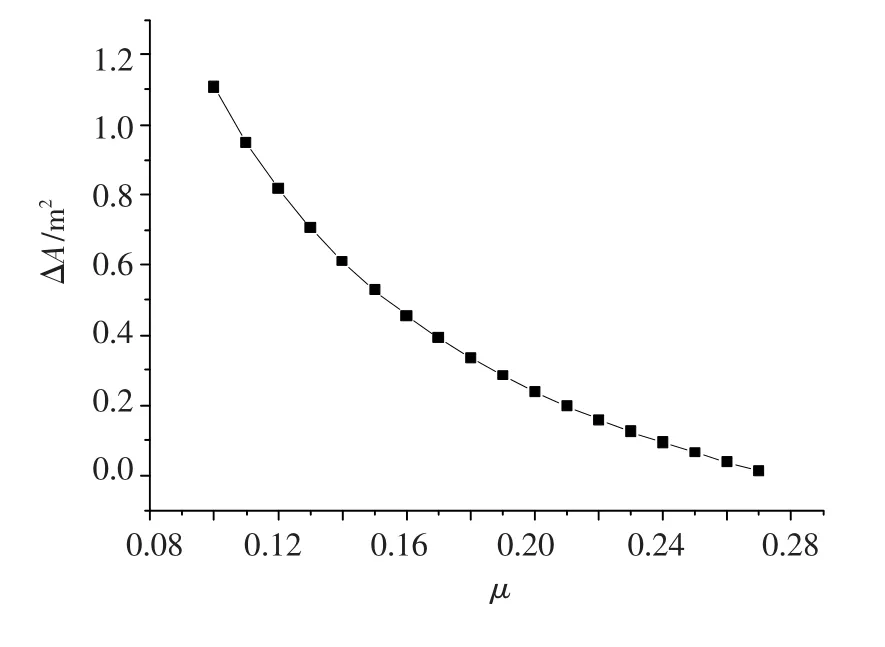
图12 ΔA与μ的关系

从图12可以看出，随着材料性能的发展和施工工艺的进步，摩阻系数μ逐渐取大值时，所需的辅助索面积也迅速减小.泰州长江大桥通过模型试验证明该桥可以取μ=0.2，此时上下游两侧辅助索的总面积ΔA=0.239 m2，即每根辅助缆索的面积仅需0.12 m2就可满足抗滑要求.从缆索的锚固方面看，这是不难做到的.此外，由于该方案前述钢结构方案的原理和构造并无冲突，因此两者还可同时采用，达到更好的效果.

4 结论

1)当采用刚性中塔时，三塔悬索桥中塔塔顶处的鞍缆抗滑安全系数K是控制设计的重要指标之一.泰州长江大桥如采用A形刚性中塔，K0.15= 1.088，K0.2=1.451，均小于规范推荐值2.0.

2)设置中央扣或在塔根和主缆之间增设扣索，对中塔处的鞍缆抗滑安全系数的影响均较小.

3)增大主缆矢跨比可以加大主缆与索鞍间切点的圆心角θ，从而提高抗滑安全系数.以泰州长江大桥为例，f/l=1/8时的抗滑安全系数比f/l=1/12时提高了27.0%.

4)在塔顶和主缆之间设置钢结构构件帮助主缆受力，可以显著提高抗滑安全系数.该构件必须能同时承受拉力、压力和弯矩，二力杆在此处是无效的.对于采用刚性中塔的泰州长江大桥，钢结构构件与主缆的夹角α=60°时效率最高，该构件最经济的特征尺寸为 A1=0.1 m2，I1= 0.25 m4.

5)在中塔鞍座和两侧主缆之间设置辅助拉索，可帮助减小主缆在活载作用下的拉力，从而提高与索鞍的抗滑安全系数.所需辅助拉索的最小面积ΔA随缆、鞍摩阻系数μ的增大而减小.泰州长江大桥取μ=0.2时，每根辅助索所需面积仅为0.12 m2.

［1］吉林，韩大章.泰州长江大桥设计［J］.现代交通技术，2008，5(3):20-28.

［2］邹敏勇，郑修典，王忠彬，等.泰州长江公路大桥三塔悬索桥中塔方案设计［J］.世界桥梁，2008(1):5-7.

［3］万田保，王忠彬，韩大章，等.泰州长江公路大桥三塔悬索桥中塔结构形式的选取［J］.世界桥梁，2008，(1):1-4.

［4］罗喜恒.基于挠度理论的三塔悬索桥参数分析［J］.建筑结构，2008，38(9):100-101.

［5］严敏国.现代悬索桥［M］.北京:人民交通出版社，2002:18-19.

［6］万田保，杨进.三塔两跨悬索桥2个重要的技术指标和中塔疲劳验算加载模式［J］.世界桥梁，2008 (1):8-10.

［7］吉林，陈策，冯兆祥.三塔悬索桥中塔主缆与鞍座间抗滑移试验研究［J］.公路，2007(6):1-6.

［8］杨进.泰州长江公路大桥主桥三塔悬索桥方案设计的技术理念［J］.桥梁建设，2007(3):33-35.

［9］阮静，吉林，祝金鹏.三塔悬索桥中塔结构选型分析［J］.山东大学学报:工学版，2008，38(2):106-111.

［10］万田保.悬索桥主鞍座的几何位移特征及与总体布置的关系［J］.桥梁建设，2003(3):28-31.

［11］中华人民共和国交通部.JTJ xxx—2002公路悬索桥设计规范(报批稿)［S］.北京:人民交通出版社，2002.

［12］王浩，李爱群，杨玉冬，等.中央扣对大跨悬索桥动力特性的影响［J］.中国公路学报，2006，19(6): 49-53.

［13］GIMSING N J.Cable supported bridges:concept and design［M］.New York:John Wiley，1997:130-133.