波浪模拟及其对水下航行体出水过程影响
2011-03-12权晓波孔德才
权晓波,孔德才,李 岩
(北京宇航系统工程研究所,100076北京,cxz0813@sohu.com)
水下航行体具备隐蔽、机动、对敌攻击具有突然性等优势,在未来战争中将发挥重要作用[1].水下航行体的出水过程是一个穿越不同介质界面,环境介质密度和运动速度等参数剧烈变化的非定常、非线性气水两相运动过程,将引起流体动力或运动载荷的大幅变化,影响水下航行体出水姿态、运动稳定性以及在空中正常飞行,甚至导致发射失败,是水下航行体水下发射的关键技术[2].文献[3]指出,水下航行体水下发射动力学与空中发射飞行器动力学由于侧向载荷分布极为不同而有很大区别.此外,水下航行体出水时的运动规律和载荷变化规律还要受到真实海况下水面波浪情况的影响,不但与波浪传播方向、浪级有关,还与其出水相位有关[2].刘曜和马震宇[4]分析了波浪力对水下航行体出水参数的影响,文献[5]研究表明,水下航行体出水俯仰角在顺/逆浪时的变化范围在±3°;田兵等[6]的仿真结果表明,水下航行体在不同海况下及不同的波浪方向角和初相位角下所受到的波浪力和波浪力矩是不同的,即波浪对水下航行体的影响具有随机性.
本文首先基于波浪理论得到了二阶Stokes波的速度表达式,并通过给定入射边界速度分布形式的方法实现波浪的数值模拟;然后利用动网格技术、UDF技术等,以五级海情为例,探讨了水下航行体模型(钝头圆柱体)出水时波浪对其三维流场、力学特性等的影响.
1 波浪模拟研究
海洋近水面处情况极为复杂,除了受自由液面影响外,还存在风、波浪、潮流、涌等多种自然现象,其中波浪对水下航行体出水过程影响较大,若忽略该因素甚至可能导致水下航行体发射失败.基于对水波方程的不同展开形式,波浪理论大致可分为线性波和非线性波2类.波面振幅较小时,线性波理论与实际波浪情况较接近,但是在波面振幅较大时,线性微幅波理论会带来较大误差.在实际海况中,波浪的波高相对于波长(或相对于水深)一般是有限的,在这种有限振幅波中,波动的自由水面引起的非线性影响必须加以考虑,即自由表面的运动条件和动力学条件是非线性的,因此对于实际海洋中的波浪进行研究需要基于非线性波理论.
1847年Stokes将摄动法用于非线性波的研究,把有限振幅的非线性波视为无限多个线性波的Fourier组合,得到了有限水深条件下的二阶解和无限水深下的三阶解,式(1)即为Stokes波的二阶解形式.
波面方程:

由于Stokes波理论适用于水深相对波长较大的深水情况[7],用于文中模拟水下航行体发射出水过程的波浪,具体做法是根据二阶Stokes波理论推导出如式(2)和式(3)所示的波面运动速度表达式.
水平速度:

垂直速度:
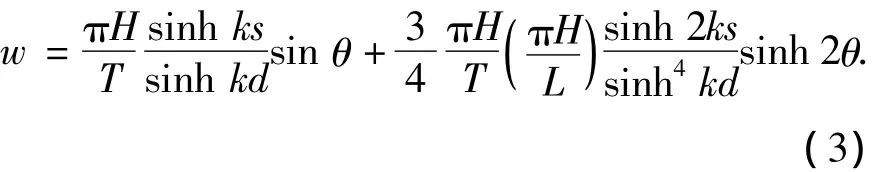
利用UDF技术将其作为入射边界条件耦合到计算方程中,从而实现非定常波浪模拟.式中H为波(浪)高,θ为相位角,L为波长,k为波数,d为不计及波面的水深,s为计及波面的水深,T为周期.
为检验上述造波方法的可行性和准确性,在二维条件下进行了验证[8~9].气、水交界面通过VOF模型进行模拟[10],所模拟的二维波浪参数为:波高为1 m,波长为9 m,周期为2.4 s,水深为5 m.考虑重力和粘性作用.计算域如图1(a)所示,为20 m×10 m,采用结构化网格划分.计算域上下边界为固体壁面,参考源项造波的方法[11],左边界给定速度入口,右边界为自由出流条件[12].计算过程中采用的湍流模型为标准k-ε模型[13].

图1 t=13.6 s时数值模拟波形及其与理论波形对比曲线
图1(a)给出了t=13.6 s时的波形图.从图中可以看到计算域中包含有2个波形,这与9 m波长、20 m计算域这一计算条件是一致的.图1 (b)为根据式(1)得到的Stokes波二阶理论解与波浪数值模拟结果的对比曲线,可以看出二者波形较为吻合,在4.3 m和13.5 m处分别形成波峰,波峰之间距离与造波时给定的9 m波长相一致.Stokes波二阶理论解是在流体无粘、无旋假设前提下通过摄动法得到的,而波浪数值仿真中则考虑了流体的粘性作用,通过N-S方程求解得到,因此,数值波高较理论波高有一定的偏差,且随着距入射边界的距离增大,这种衰减越明显.此外,从图1(b)还可看出,波峰较为尖突,波谷较为平坦,并且波峰偏离初始平衡位置的距离要大于波谷偏离平衡位置的距离,这也是符合二阶Stokes波理论波形的.无旋运动的有限振幅Stokes波的质点运动是不封闭的,在运动轨迹上部处于波峰的质点比位于波谷的轨迹下部质点运动得快一些,如图2(a)所示,一部分质点随着波浪运动被输运前进了,即Stokes波不是纯粹的振动波,而带有输移波的特征.图2(b)给出的计算结果也体现出了这一特点.综合以上分析,利用给定计算域入口速度分布造波的方法模拟出的波浪具有与理论相符且具有精度较高的特点,可以应用于工程研究.

图2 质点运动轨迹对比
2 波浪对水下航行体出水过程的影响
在上述工作的基础上,本文开展了波浪对水下航行体出水过程中的三维流场结构、力学特性、运动轨迹等的影响数值仿真研究.水下航行体的运动过程通过求解流体力学N-S方程得到,根据二阶Stokes波理论得到速度式,利用UDF技术将其作为入射边界条件,模拟五级海情下的波浪,具体参数为:水深 45 m,波高 2.65 m,周期3.58 s,波长20 m.水下航行体模型(钝头圆柱体)为水下垂直发射,发射水深为30 m,弹射速度为20 m/s,推力为105N.
计算域网格划分如图3所示,为了更为准确的模拟波面以及波浪与航行体的相互作用,网格在水面附近进行了加密处理.图3中左边界的入口涉及水气两相,通过UDF设定波面以下为水相,波面以上为气相,右边界为自由出流条件,上下边界为固体壁面条件,前后边界为对称面条件,水下航行体给定固体壁面条件.湍流模型仍采用标准k-ε模型.从相图(图4)中可以看出,本文模拟的水下航行体模型在出水时处于波谷附近.为了研究波浪对航行体出水过程的影响,还模拟了水面为静水面时的航行体出水过程,其他条件与有波浪时相同.图中x坐标为偏航方向,y坐标代表轴向,z坐标为俯仰方向,以下各图中坐标采用相同的定义.

图3 计算域网格划分

图4 t=1.13 s时相图
图5为有波浪时计算域内不同时刻的流线图,由图5可知,在水下航行体距水面较远时,航行体周围流场结构基本成轴对称形,即波浪引起的水质点运动主要集中在近水面的区域内,在距水面较远处波浪对航行体运动的影响基本可以忽略.随航行体向水面运动,受波浪引起旋涡的诱导作用,航行体两侧的附体旋涡结构差别较大,其左侧旋涡变小且逐渐脱离头部向下运动,而右侧旋涡较大且仍存在于肩部,这2个不对称的旋涡使得水下航行体受到1个绕z轴的逆时针方向的力矩影响,使其逐渐向左侧偏转.此外,波浪作用导致的航行体两侧旋涡结构的差别还与水下航行体出水相位有关,不同相位出水时的旋涡结构将会发生变化,这需要进一步的研究.

图5 不同时刻流线图
从图6所示的有无波浪时水下航行体运动轨迹曲线对比图中可看出,无波浪静水面发射时的航行体的运动轨迹近似一条直线,而有波浪存在时其运动轨迹沿x轴负向发生了偏转,水下航行体尾部完全出水后的偏移量达到1 m左右,这与水下航行体出水时位于波谷处有关.此外,由于流动的三维性,水下航行体在偏航面上也出现了轻微的偏移.

图6 水下航行体运动轨迹曲线
图7为水下航行体质心沿坐标方向的速度变化曲线,可以看出,波浪作用对水下航行体x向的速度分量影响最大,无波浪时x向速度分量基本为0,而波浪存在时,随水下航行体接近水面,x向速度分量出现负值且逐渐增加,这与图5所示的流场结构变化相符.水下航行体y向速度分量在有无波浪时变化趋势基本一致,但波浪存在时该值较大.这主要是因为水下航行体距自由水面的距离随波浪起伏运动而发生变化,且近水面的区域内流体具有一定的速度,这2个因素导致y向速度分量在数值上出现差别.在z方向,有无波浪时的速度变化均可视为三维扰动,数值不大且偏向正方向或偏向负方向都有随机性.

图7 3个方向速度变化
3 结论
1)本文基于波浪理论得到了二阶Stokes波的波面方程及其运动速度表达式,利用UDF技术将其作为入射边界条件耦合到计算方程中,实现了非定常波浪模拟,且与理论值吻合良好,精度较高.
2)数值模拟了五级海情条件下,水下航行体模型(钝头圆柱体)水下垂直发射时波浪对其三维流场、力学特性等的影响.
3)距水面较远处波浪对水下航行体运动的影响基本可以忽略;近水面时,受波浪引起的旋涡的诱导作用,航行体两侧的附体旋涡结构、所处位置等差别较大,使得水下航行体受到绕z轴的逆时针方向的力矩影响,其向左侧偏转,尾部完全出水后的偏移量达到1 m左右;由于水下航行体距自由水面的距离随波浪起伏运动而发生变化,且近水面的区域内流体具有一定的速度,水下航行体y向速度分量比无波浪时稍大.
[1]贺小艳.水下气体射流数值研究[D].北京:北京空气动力研究所,2001.
[2]殷崇一.潜射导弹发射与出水载荷研究[D].西安:西北工业大学,2004.
[3]BURGDORFO O.Hydrodynamics of unsteady underwater launched missile with trailing cavities and crossflow drag[C]//Fluid Dynamics,Plasma Dynamics,and Lasers Conference.Honolulu:AIAA,1987:AIAA Paper 87-1319.
[4]刘曜,马震宇.潜载导弹垂直发射水弹道和分离弹道研究[J].船舶工程,2005,27(3):6-9.
[5]刘曜.波浪对运载器出水姿态角的影响[J].舰船科学技术,2005,27(3):32-34.
[6]田兵,徐新琦,肖鹏飞.波浪对潜地弹道导弹出水运动的影响[J].舰船科学技术,2009,31(4):81-84.
[7]BURCE J,WEST J,THOMSON A,et al.Statistical mechanics of ocean waves[J].J Hydronautics,1975,9 (1):25-31.
[8]LI Benxia,YU Xiping.A 2-D Numerical Irregular Wave Tank and Its Verification[J].Journal of hydrodynamics,2005,17(2):222~227.
[9]BRADFORD S F.Numerical simulation of surf zone dynamics[J].Journal of Waterway Port Coastal and Ocean Engineering-ASCE,2000,126(1):1-13.
[10]ZONG Zhi,DONG Guohai.A second order volume of fluid(VOF)scheme for numerical simulation of 2-D breaking wave[J].Journal of Marine Science and Application,2007,6(2):1-5.
[11]BRORSEN M,LARSEN J.Source generation of nonlinear gravity waves with boundary integral eqution method[J].Coastal Engineering,1987,11:93-113.
[12]OJHYAMA T.Development of a numerical wave tank for analysis of nonlinear and irregular wave field[J]. Fluid Dynamics Research,1991(8):231-251.
[13]QI Peng,HOU Yijun.Numerical wave flume study on wave motion around submerged plates[J].China Ocean Engineering,2003,17(3):397-406.
