一种改进的PS-LDPC码构造法
2011-03-12刘宁庆孙浩伟
刘宁庆,王 焜,孙浩伟
(1.哈尔滨工业大学通信技术研究所,150080哈尔滨,dulubleach@126.com; 2.中国海军驻哈尔滨地区舰船配套军事代表室,150046哈尔滨)
采用和积算法(S-PA)译码的低密度奇偶校验(Low-density Parity-check,LDPC)[1]码呈现近似Shannon极限的误码率特性[2],被认为是应用于电信领域的下一代差错控制码.大周长的校验矩阵能够保证大的码字最小距离,提高译码效率并改善LDPC码的误码率特性[3].采用PEG(Progressive Edge-growth)方法可高效地构造大周长校验矩阵[4-5],却增加了LDPC译码器硬件设计的复杂度.因此构造大周长且易于硬件实现的LDPC码是目前的研究热点.
逐级构造的思想被广泛的应用于构造LDPC码[6-8]以降低LDPC码译码器硬件设计的复杂度.基于该思想,Jin Lu等[9-10]提出了一种以具有不同行(或列)移位系数的单位阵作为各级子矩阵的LDPC码,即PS-LDPC(Partition-and-Shift LDPC)码,并证明了处于同一级中的各个子矩阵之间形成闭合环的判决定理,且以该定理为基础提出了可构造任意周长校验矩阵的方法.然而,这种构造算法未提供在移位系数矩阵中寻找闭合环路的复杂过程的详细步骤,且采用判断随机数是否满足2t循环定理约束条件的方式筛选各子矩阵的移位系数,未获得最佳移位系数.
为此本文采用两种可行的方法完成矩阵中找闭合环路的过程;并详细的分析了子矩阵移位系数的选择与可能形成的闭合环之间的关系,为PS-LDPC码各子矩阵的移位系数的筛选提供了详细的判断准则,有利于构造具有更大周长的PSLDPC校验矩阵.基于上述方法构造的PS-LDPC译码器比传统构造法构造的PS-LDPC码获得了更高的译码性能.
1 相关工作
PS-LDPC码的基本原理[9]如图1所示.1种LDPC码可以由其Tanner图描述,Vc表示所有m个校验节点的集合,Vb表示所有n个信息节点的集合.可将Vc和Vb分别划分成Nb和Nc个大小均为p的子矩阵,其中m=Nc·p,n=Nb·p,且Nc≥j,Nb≥k,j、k分别表示校验矩阵的最大列重和行重.每个子矩阵中的元素被索引在0~p-1之间;在第α个校验节点子矩阵中的第Xc个校验节点在Tanner图中与第β个信息节点子矩阵中第Xb个信息节点连接,且有Xb=,其中表示模为p的加法运算.以这种形式表示的LDPC码为准循环LDPC码的一种.如将校验矩阵H划分成Nc×Nb个大小为p× p的子矩阵,每个子矩阵均为单位矩阵或其循环移动矩阵,则校验矩阵H可由这些子矩阵的移位系数Sα,β表示,即移位矩阵S=[Sα,β].一个(20,3,4)的校验矩阵的Tanner图及其移位矩阵S如图1所示.
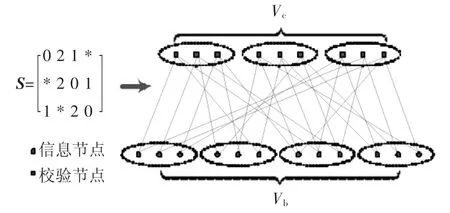
图1 (20,3,4)校验矩阵的移位矩阵S及Tanner图
图中S中的“*”代表零矩阵所对应的系数.
文献[9]提出的2t循环定理指出如果一个校验矩阵H的移位矩阵S中一个长度为2t的闭合环路上的顶点Sα1,β1,Sα2,β2,…,Sα2t,β2t满足

则这个循环移动矩阵S对应的校验矩阵中将沿着这个闭合环路形成长度为2t闭合环路.PS-LDPC码循环移动矩阵S的构造即通过考察各个长度为2t'的闭合环路是否满足2t循环定理来避免循环的产生(此处及后文所指的满足2t循环定理均指,即不会构成长度为2t的循环).文献[10]中详尽的描述了校验矩阵的构造法则,本文不予赘述.
2 移位系数的选择
文献[10]提出的获取PS-LDPC码校验矩阵H中子矩阵的移位系数的方法是合理的,但构造效率可进一步提高.下面提出一种改进的确定某子矩阵的移位系数的方法.如图2所示的4个6× 6的单位矩阵的循环移动矩阵,根据2t循环定理规定的运算准则可知:
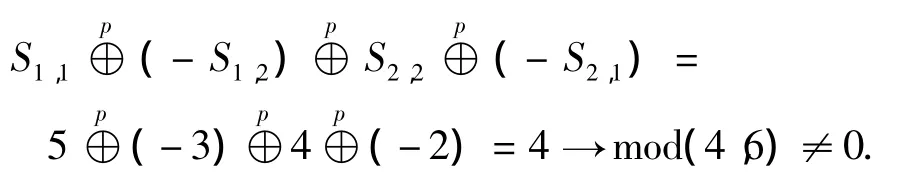
故由这4个移位系数组成的长为4的闭合环路在监督矩阵中不会形成长为4的循环.然而,由图可知这4个移位系数对应的子矩阵可形成长为12的环.此时的循环路径以2t循环定理的运算准则可表示为
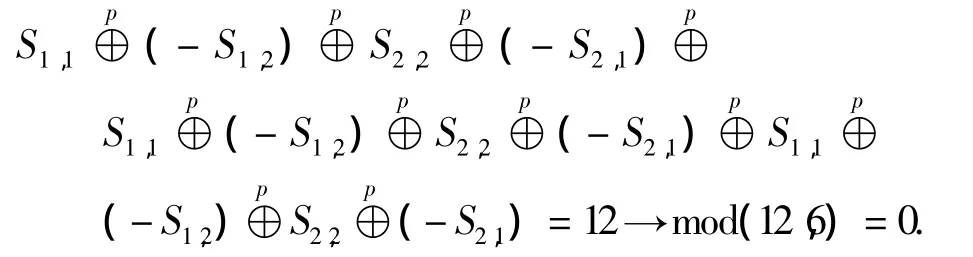
本文将不重复的闭合环路形成上的环称为一次环,而在多次重复的闭合环路上形成的环称为多次环.对于p≠1的PS-LDPC类码,多次环的形成不可避免,但可以采取措施保证其长度最大化.

图2 长为4×3的循环示例
考察类似情况,可得到如下结论:满足2t循环定理的闭合环路(长度为2t)上的顶点(不同的移位系数),形成长为L的闭合环路,其中
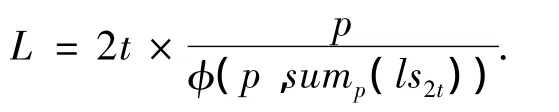
式中:p为每个子矩阵的行/列数;φ(x,y)表示x和y的最大公约数;
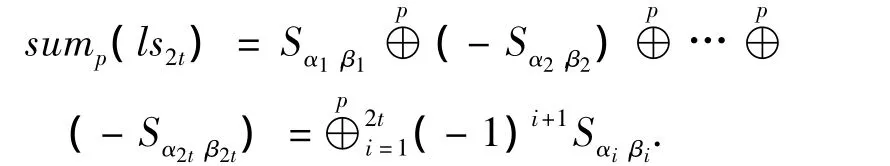
因此在规定某个子矩阵的移位系数时,应尽量选择可使sump(ls2t)与p的最大公约数较小的移位系数.当sump(ls2t)=p/2时为最不利的情况,此时循环的长度为4t.然而采用文献[10]的构造方法构造PS-LDPC码的校验矩阵时,可缩减一次判断移位系数是否满足4t长度闭合环路上的2t循环定理的过程.
基于上述思想,改进文献[10]中提出的移位矩阵的构造方法.以周长为g的校验矩阵H作为基底产生矩阵,构造PS-LDPC码校验矩阵的移位矩阵S的改进方法如改进算法1所述.

这种改进构造方法保证了每确定1个子矩阵的移位系数时,使经过该子矩阵的循环的长度最大化.其中Lmint表示起始且终止于Sr的所有长为2t'的闭合环路形成的最短的循环长度,亦即Sr取某个值时,在终始于它的所有2t'长的闭合环路上出现的最不理想情况;LMIN则表示在长度从g到gc-2的所有闭合环路上出现的最不理想情况(最短循环);选取最大LMIN对应的值为Sr保证最短循环长度的最大化.每添加1个Sr记录这个Sr对应的最大LMIN(记为max(LMIN)),构造完毕所得校验矩阵的周长g'即为最小的max(LMIN).若需要再下一级构造,则以此次构造的校验矩阵作为下一级的移位矩阵,并以g'为起始考察的闭合环路长度,至需要的周长,按改进的方法在原校验矩阵“1”的位置添加最优的Sr值.
这种改进构造法则使得构造过程更有目的性,避免了t'=r·t时出现的sump(ls2t)≠0而sump(ls2t')=0的情况,因而避免重新选择Sr的需要.因此,改进的构造法无论从校验矩阵的译码性能亦或构造效率上都有明显的进步.
此外,可采用不同的方法构造未指定周长的最上级矩阵(PS-LDPC码中可理解为未添加移位系数Sα,β前的基底移位矩阵S),如以上提出的PS-LDPC码改进构造法或PEG构造法.PEG方法构造的矩阵具有更优的周长特性,因此最上级矩阵可以采用PEG矩阵.参照第3部分介绍的寻找定长的闭合环的方法,可获取此最上级矩阵的周长g,再根据上面提出的构造法完成周长至少为gc的校验矩阵的构造.
3 闭合环路查找方法
在矩阵中寻找闭合环路是繁琐的过程,本文提出一种直观的寻找长为2t闭合环路的方法,通过改变某些参数,可寻找矩阵中经过某节点的不同历经范围内的闭合环路.
设hi,j为大小为m×n的矩阵H中的元素,欲寻找历经H矩阵的所有经过hi,j且长为2t的闭合环路,可用1个2t元矢量CP表示长为2t的闭合环路的边轨迹.CP的偶数元表示Tanner图中连接到同一个校验节点的2个信息节点作为闭合环路的2个顶点时,这2个信息节点的列数差;CP的奇数元表示Tanner图中连接到同1个信息节点的两个校验节点作为闭合环路的2个顶点时,这2个校验节点的行数差.因此CP的每一元表示了闭合环路的1条边历经的行数或列数.图3为6元矢量CP的示意图.
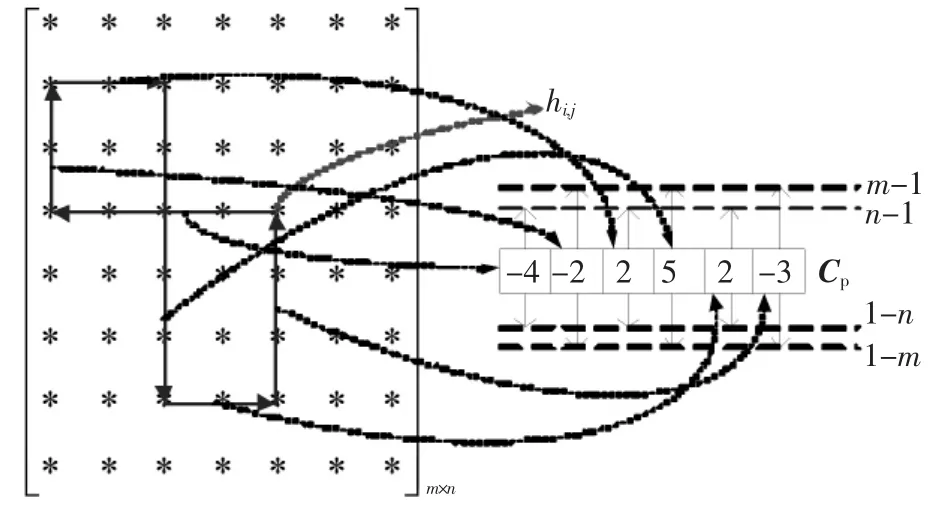
图3 长为6的闭合环路及6元矢量CP示例
此外对于历经矩阵H的闭合环路,以上对CP各元参数的限制应与H的尺寸相关,不超出H的行列范围,故另加限制条件如下:
1)偶数元取值范围为(1-n,-1)∪(1,n-1),奇数元取值范围为(1-m,-1)∪(1,m-1);
2)对于任意偶数x<2t,且k为偶数有
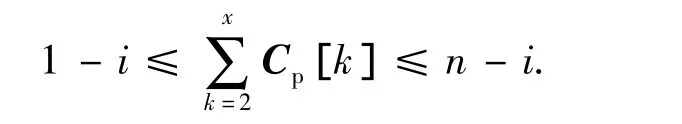
3)对于任意奇数y<2t,且k为奇数有
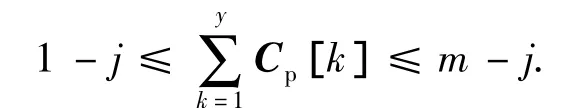
4)对于k为奇数或偶数,均有
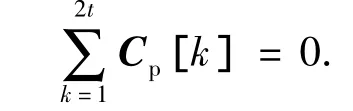
经以上限制条件,可保证长度为2t的闭合环路历经H且终始于hi0,j0.闭合环路上的顶点可表示为hiz,jz,z(1≤z≤t)表示自hi0,j0后历经的第z个顶点.对于hi,j不全为1的情况,需考察hiz,jz是否为0,hiz,jz是0则舍弃该CP.
当z为奇数时,iz=i0+∑CP[k],(k=1,3,…,z);jz=j0+∑CP[k],(k=2,4,…,z-1).
当z为偶数时,iz=i0+∑CP[k],(k=1,3,…,z-1);jz=j0+∑CP[k],k=2,4,…,z.
通过考察限制条件1)~4)获得的满足条件的矢量CP即为欲寻找的闭合环路起始于hi,j的边轨迹,进而获得闭合环路上的元素.
4 性能仿真
分别以改进构造算法和文献[10]提出的传统构造法(g>8)构造一列重1≤j≤3,行重7≤k≤9的,1 200×3 600的非规则PS-LDPC码.仿真考查不同的信噪比下通过AWGN信道时这2种码的误比特率(BER).仿真结果如图5所示.
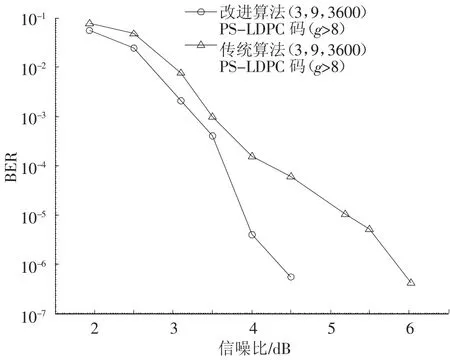
图4 AWGN信道下的BER性能比较
由图4的仿真结果可知,改进构造法构造的PS-LDPC码具有更优的译码性能,为4.5 dB信噪比时的译码性能可媲美传统PS-LDPC码Eb/No(信噪比)在5.5 dB以上时的译码性能.这也说明这样的校验矩阵H具有更大的周长和码字最小距离.
5 结论
本文通过对传统PS-LDPC码构造算法的分析,发现了传统构造算法在计算效率上的不足.并针对这个问题提出了改进算法.此外,本文介绍了一种在监督矩阵中查找闭合环路的方法,确保改进的构造算法可高效实现.最后通过对改进算法构造的PS-LDPC码的误码率特性仿真可知:
1)改进的PS-LDPC码构造算法改善了校验矩阵的周长特性;
2)改进算法提高了校验矩阵的构造效率;
3)AWGN信道下BER性能更优.
此外本文提出的闭合环寻找方法可应用在其他LDPC校验矩阵的构造算法中.
[1]GALLAGER R.Low-density parity-check codes[J]. IEEE Transactions on Information Theory,1962,8 (1):21-28.
[2]MACKAY D J C.Good error-correcting codes based on very sparse matrices[J].IEEE Transactions on Information Theory,1999,45(2):399-431.
[3]MACKAY D J C,NEAL R M.Near shannon limit performance of low density parity check codes[J].Electronics Letters,1997,33(6):457-458.
[4]HU X Y,ELEFTHERIOU E,ARNOLD D M.Progressive edge-growth Tanner graphs[C]//IEEE Global Telecommunications Conference,2001.GLOBECOM'01:IEEE. Piscataway:IEEE,2001,2(25-29):995-1001.
[5]HU X Y,ELEFTHERIOU E,ARNOLD D M.Regular and irregular progressive edge-growth tanner graphs[J].IEEE Transactions on Information Theory,2005,51(1):386-398.
[6]ZHANG Tong,PARHI K K.An FPGA implementation of(3,6)regular low density-parity check-code decoder[J].EURASIP Journal on Applied Signal Processing,2003,6:530-542.
[7]LIAO E,ENGLING Y,NIKOLIC B.Low-density parity-check code constructions for hardware implementation[C]//IEEE International Conference on Communications.Piscata way:IEEE,2004,5:2573-2577.
[8]LI Z W,VIJAYA KUMAR B V K.A class of good quasi-cyclic low-density parity check codes based on progressive edge growth graph[J].IEEE Commun Lett,2004,2:1990-1994.
[9]LU J,MOURA J M F.Partition-and-Shift LDPC Codes[J].IEEE Transactons on Magnetics,2005,41(10): 2977-2979.
[10]LU J,MOURA J M F.Structured LDPC codes for highdensity recording:Large girth and low error floor[J]. IEEE Transactions on Magnetics,2006,42(2):208-213.
