稀有事件logistic回归在医学研究中的应用*

赵晋芳 罗天娥 范月玲 曾 平 仇丽霞 刘桂芬△

如果疾病的发生水平很低，极为不常见，病例在人群中所占比重就非常小，那么称这个医学事件为稀有事件。如果我们采用常见的现况流行病调查方法或队列研究研究这种疾病，就会导致收集的数据中病例数与非病例数很不均衡。比如要探索研究该疾病的影响因素，通常的做法是对病例和非病例的两类人群建立logistic回归模型，然而由于资料中的病例所占的比例远远低于非病例的比重，这就给稀有事件的统计分析带来一系列问题，在这种情况下仍采用常规的logistic回归方法就不适合了。本文将主要探讨一种适用于解决医学现象研究中稀有事件的logistic回归模型，它校正了普通logistic回归在参数估计、统计推断和概率预测方面都有可能存在的缺陷。

原理和方法

1．稀有事件logistic回归

医学研究中，当随机反应变量Y的结果表现为二分类变量时，如发病(Y=1)和不发病(Y=0)，感染(Y=1)和不感染(Y=0)，若感染(Y=1)的概率P受到因素影响时，可表示为

x'为暴露因素，α，β分别为截距项和回归参数向量。logistic回归系数的极大似然估计值^β具有一致性、渐近有效性和渐近正态性的性质，并且在结果变量Y两类取值频率相等时的检验效率是最高的〔1－3〕。

但在稀有事件分析中，由于存在大量Y=0的记录，而Y=1的例数却很少，这就会导致一般的logistic回归在参数估计、统计推断和概率预测方面都可能存在一定的缺陷。下面介绍一种适合医学中稀有事件的logistic回归(rare event logistic，re-logistic)，其基本思想是在普通logistic回归结果基础上给予适当的校正。

(1)先验校正

先验校正(prior correction)是在普通logistic回归最大似然估计值的基础上，结合总体中Y=1的概率τ，以及样本中Y=1的比例(或叫抽样概率)¯y对回归系数的最大似然估计值进行校正〔4〕。~

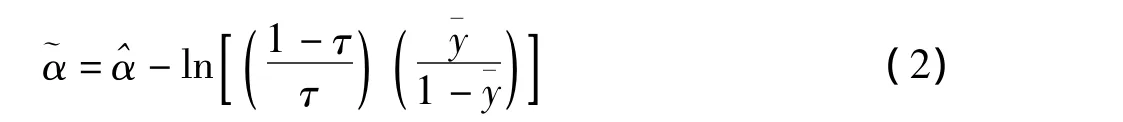
α为经过先验校正的截距项。先验校正的思想最初源于 Prentice和 Pyke(1979)，Manski和 Lerman(1977)，以及Daniel McFadden尚没有公开发表的一篇文献〔5－7〕。先验校正需要已知总体率τ，关于总体中Y=1的概率τ的先验信息可以从普查、大样本的随机抽样研究或病例－队列研究中得到。

(2)加权校正

研究中可能存在由于样本选择的原因而导致总体概率τ和样本概率¯y之间有差异，而加权校正(weight correction)正是要对样本观察单位给予合适的权重来补偿因选择偏倚造成的影响。对样本中Y=1的观察单位给予权重w1=τ/¯y，Y=0的观察单位给予权重w0=(1－τ)/(1－¯y)。则logistic回归有以下的加权对数似然函数:

最大化(3)式即可得到参数的最大似然估计值。研究表明，加权校正在大样本和模型指定有误时要优于先验校正〔8〕，而在小样本时，先验校正要优于加权校正，但这种差别不是很大〔9，10〕。

(3)稀有事件回归系数的MCN校正

α和β的最大似然估计值在小样本时是有偏的，而且稀有事件会进一步放大这种偏倚。在小样本稀有事件中，先验校正和加权校正仍存在一定的偏差，尚需要进行进一步的校正。小样本的稀有事件回归系数的偏倚量(bias)〔4，11，12〕:)式中ξi=0.5Qii［(1+w1)^πi－w1］，Qii为矩阵Q=X(X'WX)－1X'的对角元素，W=diag{^πi(1－^π)wi}。从式(4)可见，实际上偏倚量bias(^β)就是以X为自变量，ξ为应变量，W为权重的回归方程的系数的加权最小二乘估计值。校正的参数估计值为:

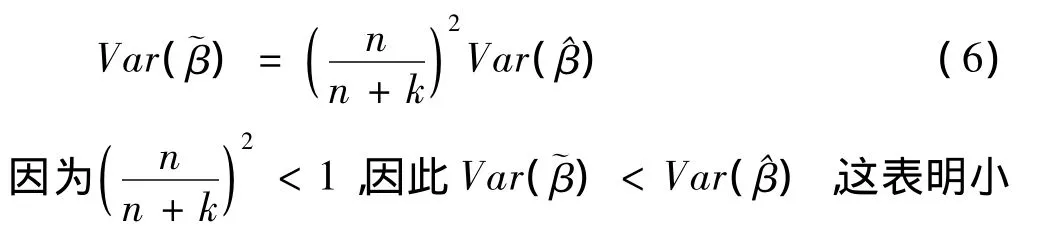
校正的参数方差矩阵为:样本的稀有事件回归系数的校正不但得到了无偏的参数估计量，而且还降低了方差，其统计性质优于前者。这种校正方法又被Gary King和Lang che Zeng简称为MCN校正(McCullagh Nelder Correction)。

(4)稀有事件概率估计

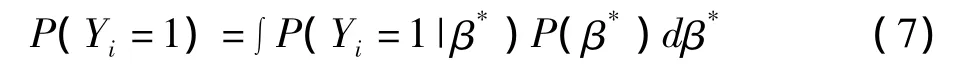
稀有事件回归系数的最大似然估计值^β本身是有偏估计值，因此个体Y=1的概率估计也是有偏的;即使^β是无偏估计值，也并不能保证概率估计值就是最优的。可以选择下面的公式估计稀有事件中Y=1的概率:β*为结合哑变量(integration dummy)。式(7)可以看做 ~β 抽样分布下 ~P(Y=1|~β)的期望值，而 ~P(Y=1|~β)是Pi=P(Y=1|β)的点估计值。式(7)亦可以近似表示为:P(Yi=1)≈~Pi+Ci或 P(Yi=1)≈~Pi－Ci。其中，Ci称为校正因子(correction factor)，计算公式为:

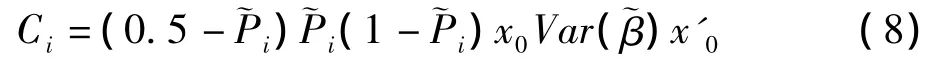
在满足一定条件下，~Pi－Ci是近似无偏的，但是模拟研究显示~Pi+Ci有更小的均方误。~Pi－Ci称为Pi=P(Y=1|β)的近似无偏估计值(approximate unbiased estimator)，~Pi+Ci称为近似 Bayes估计值(approximate Bayesian estimator)〔4〕。有研究显示，除了某些特殊情况，如多个小样本的meta分析中，近似无偏估计值要好于Bayes估计值外，多数应用中，Bayes估计值要优于近似无偏估计值。

2．非嵌套模型Vuong检验

采用Vuong(1989)提出的非嵌套模型检验(nonnested models test)〔13－15〕来检验 logistic 回归和稀有事件logistic回归的非嵌套关系。

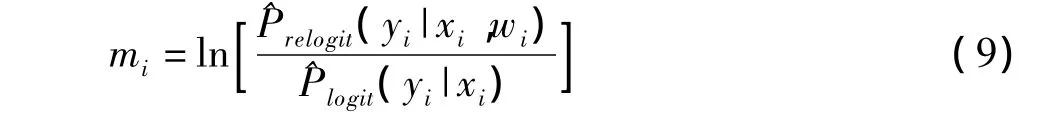
式中，^Prelogit(yi|xi，wi)和 ^Plogit(yi|xi)分别为稀有事件logistic回归和普通 logistic回归预测概率。根据Vuong，模型1相对于模型2的非嵌套模型检验的统计量为

实例分析

通过与山西省疾病预防控制中心联合，对山西省运城市五个项目防治县的316例HIV/AIDS患者进行结核病的筛查。欲对HIV/AIDS患者是否患结核病进行分析，结果如下。Min Max

表1 HIV/AIDS患者资料简单描述¯

n x±s

表2 HIV/AIDS患者资料变量编码及构成

HIV/AIDS患者中大多是初中文化程度，占总患者的66.14%(209/316);患者的平均年龄为41.6岁，以壮年为主;HIV/AIDS患者 CD4计数的均值为317.85(个/μl)，低于正常人水平，其最大值为1125(个/μl)，最小值为 1(个/μl)，标准差为 183.80(个/μl)，变异较大，因此对CD4作自然对数转换，并在以后的分析中代替CD4作为自变量，且仍用CD4作为其变量名。

调查的316例HIV/AIDS患者中仅有11人是结核感染者，感染率大约为3.48%。因此我们认为分析样本中HIV/AIDS患者感染结核是稀有事件。

表3 普通logistic回归参数估计

普通logistic回归参数估计显示HIV/AIDS患者CD4计数有统计学意义，与是否感染结核病有关系，CD4计数对数值每增加一个单位，HIV/AIDS患者感染结核的危险性降低71.1%［1－exp(－1.240412)］，即CD4计数水平越高HIV/AIDS患者患结核病的可能性越小。

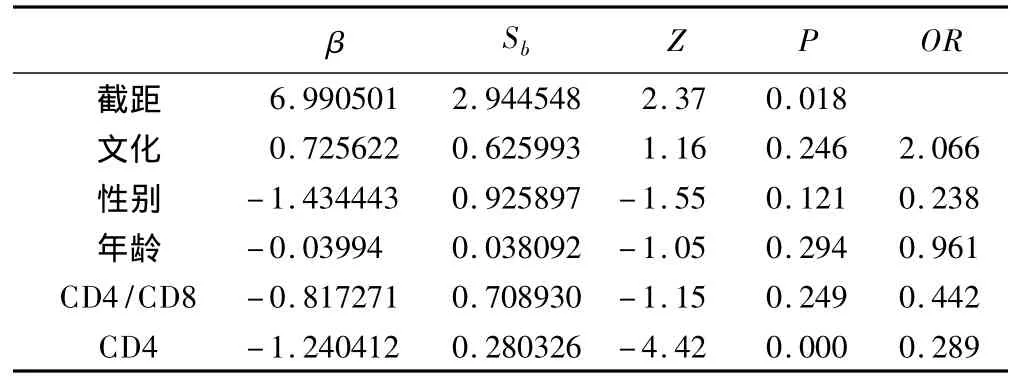
表4 logistic回归先验校正

logistic回归先验校正是在普通logistic回归参数估计的基础上对截距项做了校正，其他回归系数估计值和标准误均未发生改变。以往报道表明，感染了结核菌的HIV/AIDS患者每年发展为结核病的机会为7%，据山西省权威机构2008年底提供的数字显示，HIV/AIDS患者的结核发病率估计在5%左右，故本次研究τ取值为0.05。校正后的截距为:

表5 logistic回归MCN先验校正

logistic回归MCN先验校正参数估计CD4计数对数值每增加一个单位，HIV/AIDS患者感染结核的危险性降低68.0%。

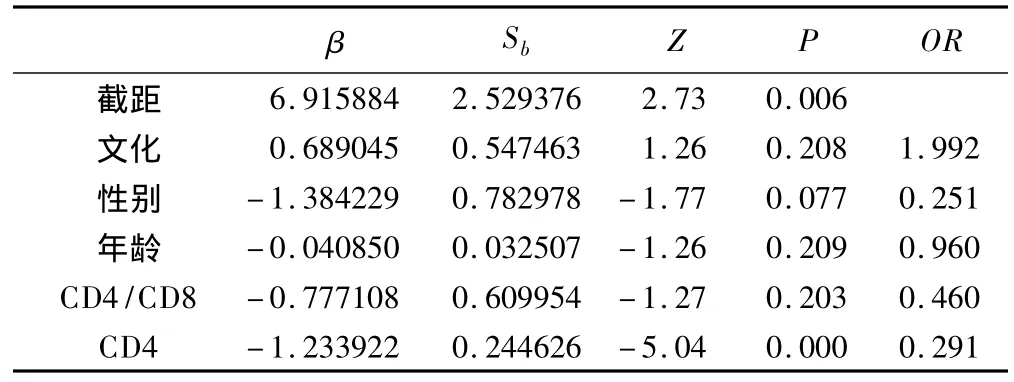
表6 logistic回归加权校正

在普通logistic回归的基础上对样本中的每个观察单位进行加权校正，其中:w1=τ/¯y=0.05/0.03481013，w0=(1－τ)/(1－¯y)=(1－0.05)/(1－0.03481013)。

加权校正logistic回归表明CD4计数对数值每增加一个单位，HIV/AIDS患者感染结核的危险性降低70.9%。

加权logistic回归MCN校正结果表明CD4计数对数值每增加一个单位，HIV/AIDS患者感染结核的危险性降低67.8%。

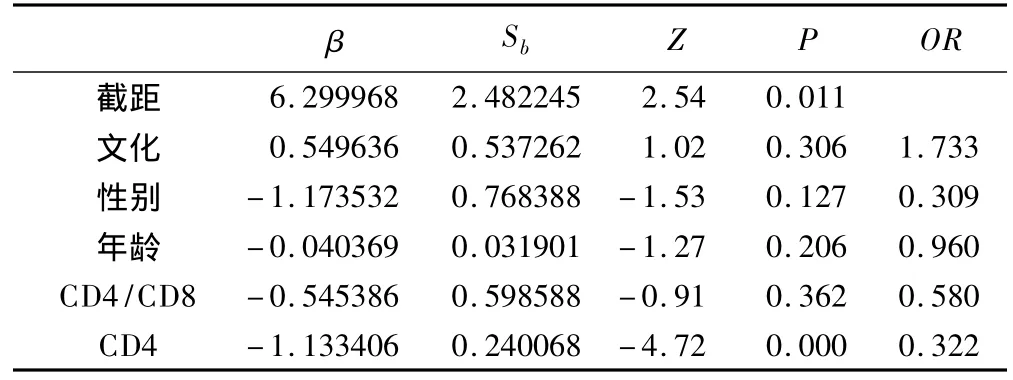
表7 logistic回归MCN加权校正

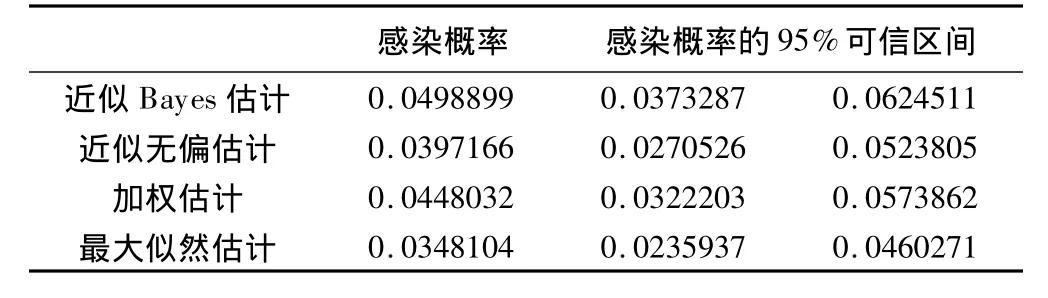
表8 HIV/AIDS患者结核感染概率估计

我们采用以上的几种模型估计本次调查样本的HIV/AIDS患者结核感染率，不同方法的HIV/AIDS患者结核感染概率估计显示，最大似然估计的感染概率最小，即普通logistic回归低估了感染概率，其他三种估计方法的感染概率估计值有所提高，弥补了稀有事件中传统的估计方法可能会低估事件Y=1的预测概率的缺憾，即校正后感染概率估计偏倚减少。加权估计和近似Bayes估计的感染概率估计值接近5.00%。

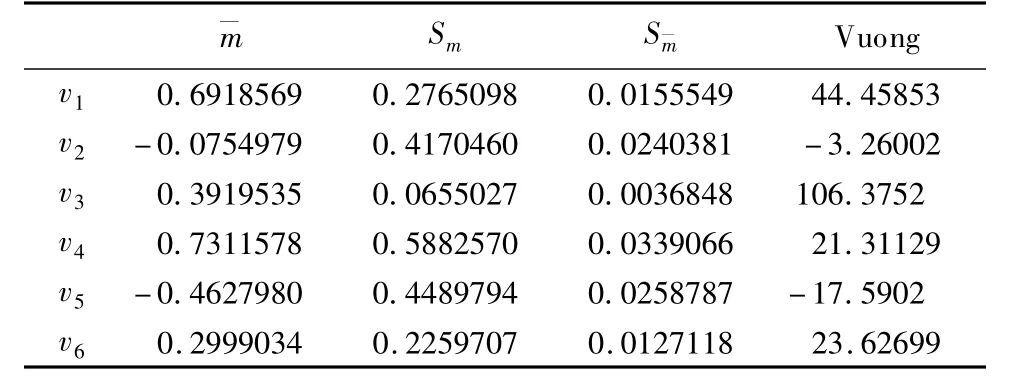
表9 不同校正方法的logistic回归和普通logistic回归的Vuong检验

PPLUS表示近似Bayes估计概率，PJIAN表示近似无偏估计概率，PROB表示加权估计概率，P0为普通logistic回归预测概率。

Vuong检验显示加权校正和近似Bayes估计都要优于普通logistic回归、近似无偏估计;近似Bayes估计优于加权校正;而近似无偏估计不如普通logistic回归。

综上，Vuong检验和概率预测结果显示近似Bayes估计得到的结果最优。

讨 论

医学研究中经常遇到二分类反应变量资料采用logistic回归分析，若应变量两类取值频率相差特别悬殊时，普通logistic回归不仅参数估计有偏，并且可低估稀有事件的发生概率。通过稀有事件logistic回归校正参数和概率估计值来解决这个问题，效果较好。实例分析结果表明，在稀有事件的分析中，不管是在模型的整体表现或者是模型的预测预报方面，稀有事件的logistic回归确实要更优于普通的logistic回归。因此对于医学中很多不常见疾病的研究，稀有事件的logistic回归是一种值得推广应用的统计模型。当然，对于某一个医学事件要根据具体的情况从专业的角度判断其是否是稀有或罕见事件，从实际应用看确定这一点并不难。

稀有事件logistic的校正方法可以在Gary King和Langche Zeng 2001年推出的 STATA程序——relogit中实现，relogit是一种非官方的程序需要下载安装后才可以使用。不同模型间的Vuong检验目前尚无专门的程序，本文通过SAS9.1软件编程实现非嵌套模型的比较。

1．Manski CF，McFadden D．Structural analysis of discrete data with econometric applications．MA:Cambridge:MIT Press，1981:51-111．

2．Imbens GW．An efficient method of moments estimator for discrete choice models with choice-based sampling．Econometrica，1992，60(5):1187-1214．

3．陈峰．医用多元统计分析方法．北京:中国统计出版社，2001．

4．King G，Zeng LC．Logistic regression in rare events data．Political analysis，2001，9(2):137-163．

5．Prentice RL，Pyke R．Logistic disease incidence models and case-control studies．Biometrika，1979，66(3):403-411．

6．Manski CF，Lerman SR．The estimation of choice probabilities from choice based samples．Econometrica，1977，45(8):1977-1988．

7．Manski CF，McFadden D．Structural analysis of discrete data with econometric applications．MA:Cambridge:MIT Press，1981:2-50．

8．Xie Y，Manski CF．The logit model and response-based samples．Sociological Methods Research，1989，17(3):283-302．

9．Amemiya T，Vuong QH．A comparison of two consistent estimators in the choice-based sampling qualitative response model．Econometrica，1987，55(3):699-702．

10．Scott AJ，Wild CJ．Fitting logistic models under tuberculosis-control or choice based sampling．J R Statist Soc B，1986，48(2):170-182．

11．McCullagh P，Nelder JA．Generalized Linear Models．New York:Chapman ＆ Hall，CRC，1999．

12．King G，Zeng LC．Explaining rare events in international relations．International Organization，2001，55(3):693-715．

13．Strazzera E，Genius M．Evaluation of likelihood based tests for non-nested dichotomous choice contingent valuation models．Working Paper CRENoS，2000:2-28．

14．Greene WH．Accounting for excess zeros and sample selection in Poisson and negative binomial regression models．Working Paper No．EC-94-10，Department of Economics，Stern School of Business，New York University，1994．

15．Vuong QH．Likelihood ratio tests for model selection and non-nested hypotheses．Econometrica，1989，57(2):307-333．