改进非劣分类遗传算法多目标优化效果评价及程序测试*

张晓丽 陈 益 韩荣荣 周建淞 李飞莹 师先锋 仇丽霞△

多目标优化问题〔1－6〕即寻找一组既满足约束条件又使总目标函数最优化的决策变量的取值，其中组成总目标函数的元素是子目标函数。进行多目标优化时我们希望找到一组可供选择、非受控的解方案集，即当考虑所有目标时，搜索空间中没有其他方案能优于它，这样的解方案集我们称为Pareto最优解集;Pareto最优解集不是由人来主观判断而是根据多目标问题优化解的自身特性来搜索的多目标有效解集的范围，为决策者提供不止一种可供选择的方案。在医药学研究领域中存在大量的多目标优化分析问题，如药物有效成分最优提取条件、分子生物学最优试验条件、公共卫生资源的最优分配、诊断试验最优决策值、疾病最优治疗方案等。经典的多目标进化算法主要有加权法、约束法和目标规划法等，这些优化分析都是将多目标问题转化为一个或一系列的单目标优化问题〔7〕，从而利用已经成熟的单目标优化方法来间接地加以解决。但这些方法都存在明显的缺陷，主要表现在:(1)权值系数的选取主观性较强，优化结果受该系数的影响较大;(2)不同性质的目标具有不同的量纲，很难做比较;(3)各个目标函数之间通过决策变量相互关联，拓扑结构十分复杂，往往在某一个目标上是最优的，而在另一个目标上可能是最差的，不能保证所有目标都存在最优解;(4)最终只能得到一个最优解，没有可供选择的方案。另外，还要求对多目标问题本身有较深入的了解，然后人为地确定一些重要的参数。显然，这些方法的优化结果一般不会很理想。改进非劣分类遗传算法(nondominated sorting genetic algorithm Ⅱ，NSGA-Ⅱ)〔8〕是2002年Deb等人对算法NSGA的改进，它是迄今为止最优秀的进化多目标优化算法之一，具有计算简单、利用拥挤距离来代替适应度共享、引入精英策略等优点，可以为决策者提供一系列的Pareto非劣解，解决了困扰运筹学理论界的多目标优化问题。但大多数应用者对其方法的效果尚不清楚，也没有方便可行的程序，限制了该方法的推广。本文旨在应用测试函数对NSGA-Ⅱ的效果进行评价，对课题组成员英国Glasgow大学软件工程师陈益利用Matlab2009a编写的外挂SGALAB工具箱beta5008进行可靠性测试，为NSGA-Ⅱ的实际应用提供理论依据及可行的程序。

NSGA-Ⅱ方法原理

改进非劣分类遗传算法(NSGA-Ⅱ)是在非劣分类遗传算法(nondominated sorting genetic algorithm，NSGA)的基础上提出来的，它针对NSGA的三个弊端(计算复杂度较高，为O(mN3)，没有采用精英策略，需要特别指出共享半径)提出了改进方法:(1)提出了快速非支配排序方法，降低了算法的计算复杂度，由原来的O(mN3)降到O(mN2)，其中，m为目标函数的个数，N为种群大小。(2)提出了拥挤度和拥挤度比较算子，代替了需要指出共享半径的适应度共享策略，并在快速排序后的同级比较中作为胜出标准，使准Pareto域中的个体能扩展到整个Pareto域，并均匀分布，保持了种群的多样性。(3)引入精英策略，扩大采样空间。将父代种群与其产生的子代种群组合，共同竞争产生下一代种群，有利于父代种群中的优良个体进入下一代，并通过对种群中所有个体分层存放，使得最佳个体不会丢失，迅速提高种群水平。NSGA-Ⅱ流程见图 1〔8〕。

首先将第t代产生的新种群Qt与父代Pt合并组成Rt，种群大小为2N。然后Rt进行非支配排序，产生一系列非支配集Fi并计算拥挤度。由于子代和父代个体都包含在Rt中，则经过非支配排序以后的非支配集F1中包含的个体是Rt中最好的，所以先将F1放入新的父代种群Pt+1中。如果F1的大小小于N，则继续向Pt+1中填充下一级非支配集F2，直到添加F3时，种群的大小超出N，对F3中的个体进行拥挤度排序，取前N－|Pt+1|个个体，使Pt+1个体数量到达N。然后通过遗传算子(选择、交叉、变异)产生新的子代种群Qt+1。

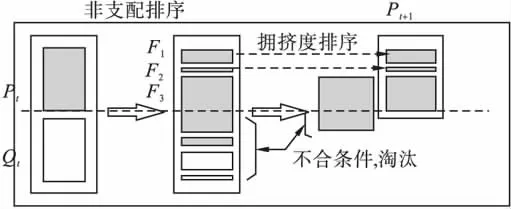
图1 NSGA-Ⅱ流程

测试方法与步骤

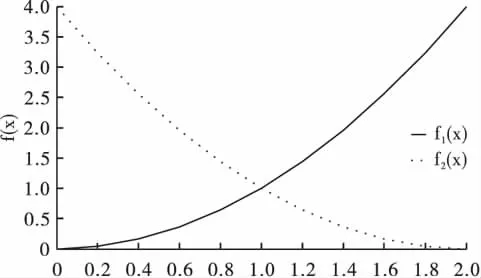
图2 两目标简单测试函数F1曲线图

2．遗传算法参数设置

采用二进制编码，取初始种群(population)=30，进化代数(generation)=100，单点交叉概率(probabili-时决策变量x的取值水平。

由图2直观分析可见，f1(x)是增函数、f2(x)是减函数，这两个目标是相互冲突的。当x=2时，f1(x)有最大值4，f2(x)有最小值为0;当x=0时，f1(x)有最小值0，而f2(x)有最大值4;在交叉点x=1处，两目标函数值均为1。决策变量在1附近时，两目标函数值均较大。

(2)两目标复杂测试函数〔8〕及其特点

在xi∈［－4，4］范围内，求解当两个目标函数均最小时决策变量xi的取值水平。由于两目标函数都含有三个自变量，我们无法画出它们的三维图，因此不能直观地观察目标函数的解空间，但是通过查文献我们知道函数F2的优化解空间为:

ty-crossover)=0.90，变异概率(probability-mutation)=0.01，简单测试函数优化运行20次，复杂函数优化运行100次。

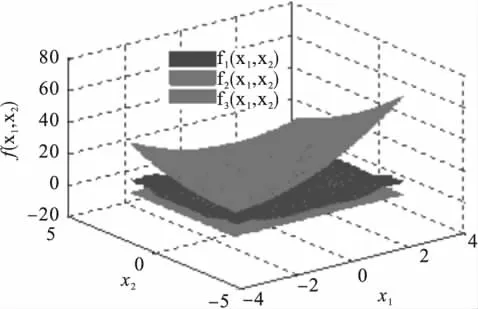
图3 三目标测试函数F3三维图

3．遗传算法性能评价

(1)在线性能评价 采用平均适应度进化曲线评价算法的动态性能。

(2)离线性能评价 采用最大适应度进化曲线反映解的变化，评价算法的收敛性。

4．软件及统计分析

选用数学功能较强的美国矩阵实验Matlab2009a软件绘制函数图形;课题组成员英国Glasgow大学软件工程师陈益利用Matlab2009a编写的外挂SGALAB工具箱beta5008完成遗传算法寻优;SPSS13.0软件进行统计分析。

测试结果

1．NSGA-Ⅱ求解两目标简单测试函数F1的Pareto非劣解集

利用NSGA-Ⅱ给出的两目标简单测试函数F1的20个Pareto非劣解方案见表1，其中6、8、13号方案与两函数交叉点解的近似度较好，其他方案为研究者提供了很好选择机会;图4、图5为其中一个方案的世代进化曲线图，可以看出，最大适应度、平均适应度曲线大约在进化5代以后就稳定在1的附近，反映了NSGA-Ⅱ具有较好的收敛性，动态性能好;图6为NSGA-Ⅱ搜索的Pareto非劣解前端图，非劣解前沿呈一条光滑曲线分布，表面大多数非劣解都可以搜索到，体现了两个相互矛盾的目标函数解的关系。由表2可知，20次随机搜索结果决策变量的平均水平为1.08，标准差为0.16，95%非劣解分布范围在0.75～1.35，包含交叉点1，两目标函数均最大的非劣解在1的附近，符合两目标简单测试函数的特点。因此，NSGA-Ⅱ能够给出合理的Pareto解集。

图4 两目标简单函数NSGA-ⅡMAX Fitness-Generation

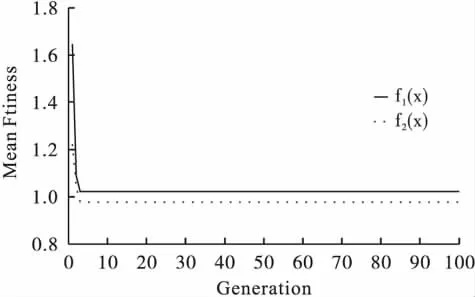
图5 两目标简单函数NSGA-ⅡMEAN Fitness-Generation

2．NSGA-Ⅱ求解两目标复杂测试函数F2的Pareto非劣解集

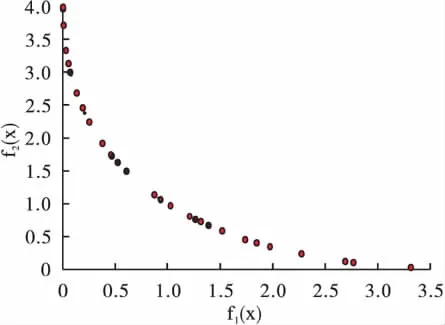
图6 NSGA-Ⅱ求解两目标简单函数Pareto非劣解前端分布

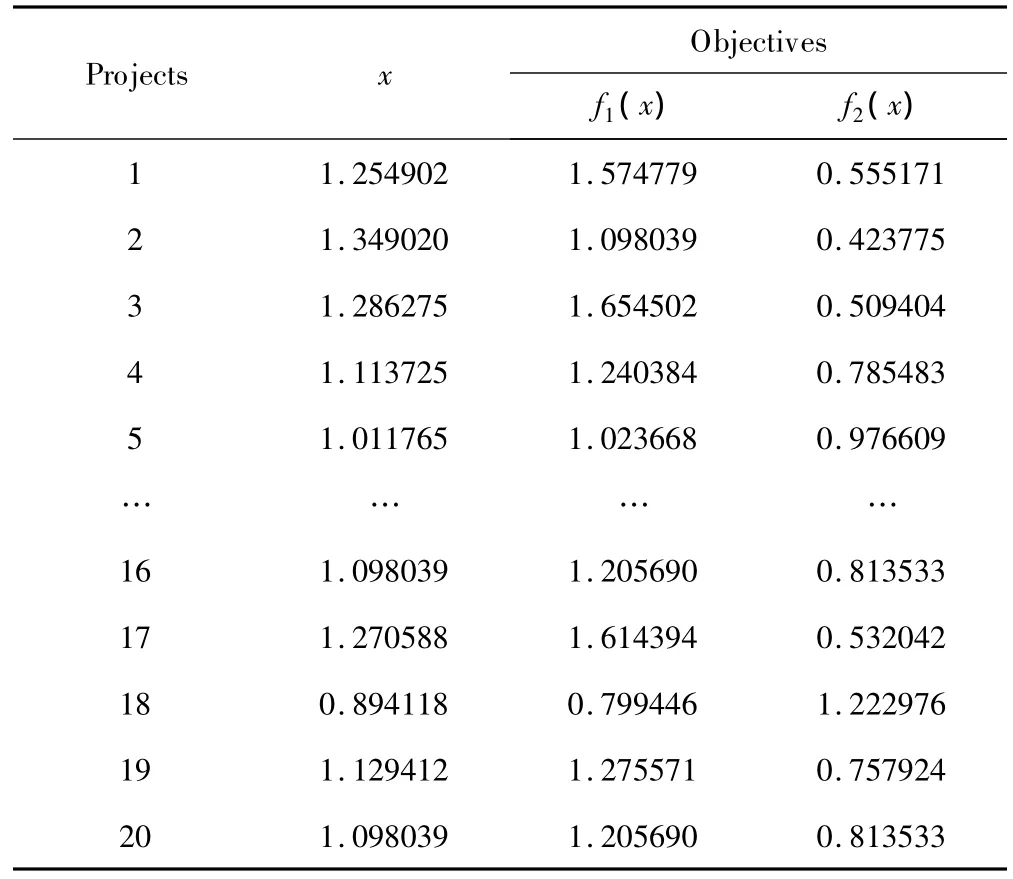
表1 NSGA-Ⅱ求解两目标简单测试函数的Pareto非劣解

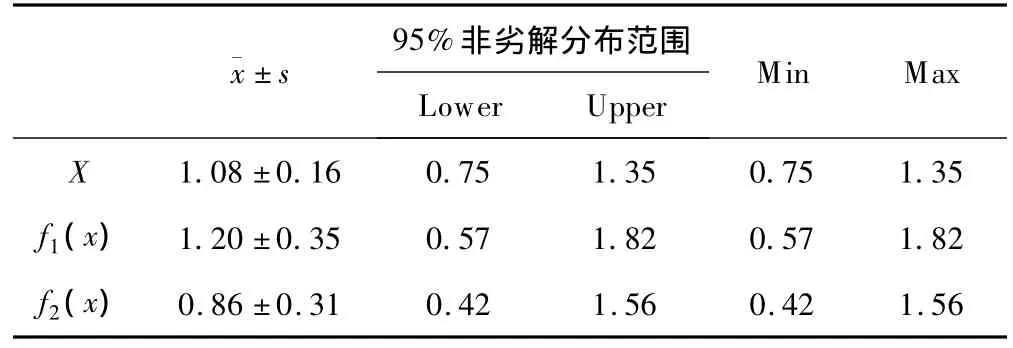
表2 两目标简单测试函数的目标函数值及Pareto非劣解平均水平

利用NSGA-Ⅱ搜索使复杂测试函数F2的两个目标函数同时最小的100个Pareto非劣解方案见表3。从其中一个方案的世代进化曲线(图7、图8)可知，目标函数f1(x1，x2，x3)最大适应度曲线大约在进化10代以后就稳定在函数值为0.65的水平附近，平均适应度曲线大约在进化10代以后就稳定在函数值为0.85的水平附近，而f2(x1，x2，x3)的最大适应度曲线大约在进化10代以后就稳定在函数值为0.7的水平附近，平均适应度曲线大约在进化10代以后就稳定在函数值为0．9的水平附近，图7反映出算法具有较好的收敛性，图8反映了算法的动态性好;图9为NSGA-Ⅱ非劣解前端图，其解前端在小于1的范围内呈下降趋势分布，显示了两目标互为冲突的特点，很好地反映了两目标间的关系。表4给出NSGAⅡ100次随机搜索结果的平均水平:在x1=0.29，x2=0.25，x3=0.41时，f1(x1，x2，x3)、f2(x1，x2，x3)均较小，分别为 0.20，0.91。NSGA-Ⅱ给出的Pareto解集中，使得两个目标都达到较小的解均在标准的非劣解范围内。研究者可以根据实际情况进行合理的选择。

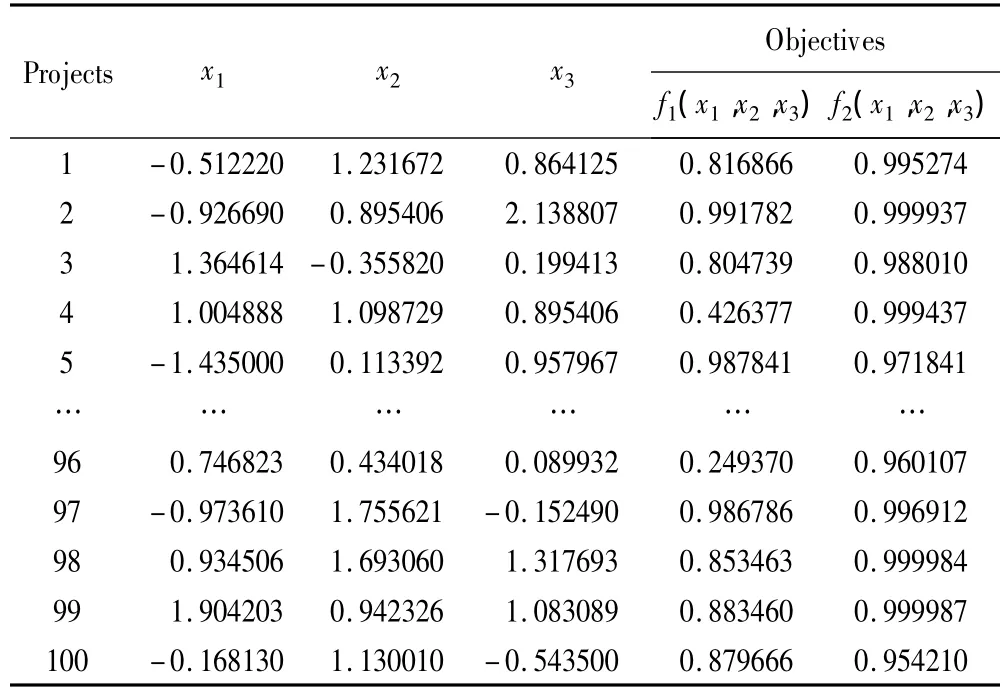
表3 NSGA-Ⅱ求解两目标复杂函数的Pareto非劣解

表4 两目标复杂函数解及Pareto非劣解平均水平

图7 NSGA-ⅡMAX Fitness-Generation

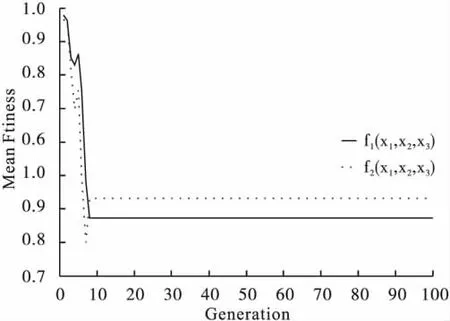
图8 NSGA-ⅡMEAN Fitness-Generation

图9 NSGA-Ⅱ求解两目标复杂函数Pareto非劣解前端分布

3．NSGA-Ⅱ求解三目标复杂测试函数F3的Pareto非劣解集

利用NSGA-Ⅱ搜索的使复杂测试函数F3三个目标同时最小的100个Pareto非劣解方案见表5;从其中一个方案的世代进化曲线(图10、图11)可知，目标函数f1(x1，x2)最大适应度曲线大约在进化3代以后就稳定在函数值为0的水平附近，平均适应度曲线大约在进化5代以后就稳定在函数值为0的水平附近;f2(x1，x2)的最大适应度曲线大约在进化5代以后就稳定在函数值为17的水平附近，平均适应度曲线在进化5代之前就稳定在函数值为17的水平附近;而f3(x1，x2)的最大适应度曲线大约在进化1代以后就稳定在函数值为0的水平附近，平均适应度曲线在进化5代之前就稳定在函数值为0的水平附近，图10的最大适应度曲线反映出算法具有较好的收敛性，图11的平均适应度曲线反映了算法的动态性好;图12为NSGA-Ⅱ非劣解前端图，其解前端是一个非线性的，非对称的三维曲面，符合三目标理论解集的分布情况。表6是NSGA-Ⅱ对三目标函数100次随机搜索结果的平均水平:x1=－0.21，x2=－0.30时，三目标函数值 f1(x1，x2)、f2(x1，x2)、f3(x1，x2)均较小，平均水平分别为0.20，15.96，－0.08。标95%非劣解分布范围为:(－2.27，1.44)，(－1.64，2.06)，(－0.10，0.18)与三目标复杂测试函数三维图(图3给出的Pareto非劣解集xi∈(－2，1))基本一致，因此，NSGA-Ⅱ给出了三个目标函数均较小的Pareto解集，同时，研究者可以根据研究问题的实际需要，在NSGA-Ⅱ给出Pareto解集中进行合理的选择。

图10 三目标函数NSGA-ⅡMAX Fitness-Generation

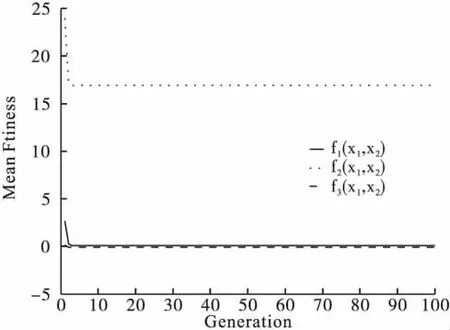
图11 三目标函数NSGA-ⅡMEAN Fitness-Generation

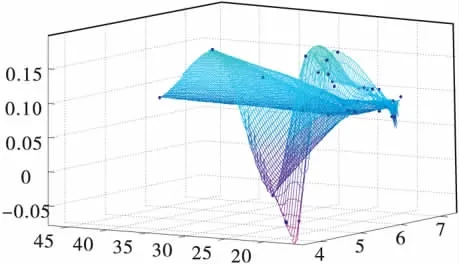
图12 NSGA-Ⅱ求解三目标函数Pareto非劣解前端分布

表5 NSGA-Ⅱ求解三目标函数的Pareto非劣解

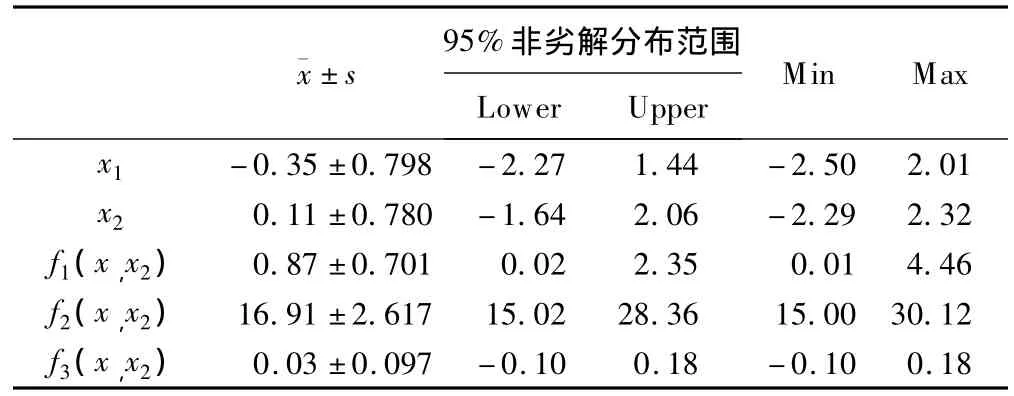
表6 三目标函数解及Pareto非劣解平均水平

结论与讨论

本文利用Matlab2009a外挂SGALAB工具箱beta5008，分别对简单两目标测试函数、复杂两目标测试函数与复杂三目标测试函数进行多目标优化。结果表明:两目标简单测试函数NSGA-Ⅱ搜索的Pareto非劣解集中目标函数值f1(x)、f2(x)基本接近于1，而且95%可信区间包含1，解前沿呈光滑曲线分布，说明该法搜索的Pareto非劣解方案合理;两目标复杂测试函数NSGA-Ⅱ搜索的Pareto非劣解集中较好的方案均在标准的优化解空间内，且分布均匀多样性好，给决策者提供了合理的选择空间;三目标复杂测试函数NSGA-Ⅱ搜索的Pareto非劣解集结合其三维空间图可知，NSGA-Ⅱ搜索的Pareto非劣解集分布在三个目标均较小的区域内，而且解前沿呈非线性，非对称的曲面分布，解集是合理的。三类测试函数的最大适应度历代进化曲线反映出了NSGA-Ⅱ具有较好的收敛性，平均适应度的历代进化曲线图均反映了算法的动态性能好。由上述测试过程可知NSGA-Ⅱ进行低维多目标优化效果理想，程序可行，可以应用于解决实际问题。NSGA-Ⅱ对于高维多目标优化的效果如何还有待进一步的测试。

1．Storn R，Price K．Differential Evolution—a Simple and Efficien tAdaptive Scheme for Global Optimization over Continuous Spaces．Technical Report，Intemational Computer Science Institute，1995(8):22-25．

2．Schittowski K．NLQPL:A FORTRAN-subroutine solving constrained non-linear Programming problems，Annals of Operations Research，1985(5):485-500．

3．Li RX，Li YU．A real time control for multi-objective optimization ofmix proportion of concrcte．Joumal of Hydraulic Engineering，1996(4):363-369．

4．De Larrardf，Sedran T．Mixture proportioning of high-performance concrete．Cement and Conerete Research，2002，32(11):1699-1704．

5．吴新余，马敏肖．遗传算法在多目标规划中的应用．南京邮电学院学报，1996(2):22-25．

6．谢敬东，王磊，唐国庆．遗传算法在多目标电网优化规划中的应用．电力系统自动化，1998，22．

7．崔逊学．多目标进Z化算法及应用．北京:国防工业出版社，2006．

8．Deb K，Agrawal S，Pratap A，et al．A fast elitist non-dominated sorting algnrithm for multi-objective optimization:NSGA-Ⅱ，Proc of the Prallel Problem Soving from Nature VI Conf，pairs，2002:182-197．

9．仇丽霞．基于遗传算法的最优决策值选择及医药学应用研究．山西医科大学博士论文，2007．

10．卢香清，谭迎军．有关多目标遗传算法的研究．南阳师范学院学报(自然科学版)，2004，(3):62-64．