基于改进夏普利值的物流企业战略联盟利益分配机制研究
2011-03-09陈向东
王 鹏,陈向东
(1.西安交通大学 管理学院,西安 710049;2.青岛远洋船员学院,山东 青岛 266071)
0 引言
近年来,战略联盟的重要性越来越受到重视。战略联盟不仅帮助企业扩大市场,形成规模和范围经济,而且改变企业组织结构和企业间关系,提高企业资源整合能力,使联盟成员收益增加。实施战略联盟策略,如何在联盟成员之间合理分配利益是联盟成功的重要因素[1]。
文科和朱延平[2]、庆艳华[3]等学者考察了供应链成员相关利益分配问题,陈功玉和王珍珍[11]研究了虚拟企业的利益分配问题,朱敏则探讨了快递企业协作模式下分配方式,提出应考查企业的风险因素[12]。从应用情况看,主要采用了联盟博弈的夏普利值法,但是忽略了夏普利值法的缺陷。由于夏普利值法中各联盟形式的结合是随机的,结成联盟的成员处于相对平等的地位,但是这与实际情况大相径庭。在实际过程中,组成战略联盟,必然有一个或若干个核心企业,他们或者具有大规模的客户群,或者拥有关键的技术,还有的拥有较强的资金运作能力等。而且在联盟中,不同企业发挥的作用,面对的风险不同。因此,在采用夏普利值方法时,需要对联盟成员的重要性加以考虑,赋以权重,这样才能更好体现企业的价值,研究也更加符合实际[4][5]。但是,如何对物流战略联盟的成员加以权重还有待解决,本文将针对此问题展开讨论。
1 战略联盟的利益分配
1.1 联盟博弈
为实现物流企业的战略联盟,本文采用联盟博弈的夏普利值方法确定利益分配方法。联盟博弈原则是:(1)联盟所获取的总体利益大于非联盟情况下各成员取得利益之和;(2)联盟利益的分配保证各成员获取利益大于非联盟情况下各成员单独获取的利益[6]。
本文以联盟博弈的基本原理为理论基础,即:二元组G≜〈N,v〉称为局中人集合N上的联盟博弈,如果v是N的所有子集形成的集合2N上的映射,满足:①v(φ)=0;②对所有,只要S∩W=φ,则有v(S∪W)≥V(s)+v(W)。称映射v为特征函数,称N的任何非空子集为联盟。性质②表明联盟博弈通过合作使总收益不致减少。
当N给定时,在集合Γ{≜{v|〈N,v〉为N上的联盟博弈}上存在唯一映射φ:Γ→RN,其中φ=(φ1,φ2,…,φn)满足有效性,对称性和可加性公设,φi有表达式:

其中,▽i(T)=v(T)-v(T{i});i=1,2,…,n。
称映射φ为夏普利值向量映射,称φ[v]=(φ1[v],φ2[v],…, φn]v[)为博弈的夏普利值,每个分量为夏普利指数。T是博弈〈N,v〉的联盟。|T|是T中含有的元素数量。
1.2 修正夏普利值
夏普利值法利益分配的优点是可以保证联盟成员获取的利益不低于非联盟情况下该成员获取的利益。但是,夏普利值方法假设联盟成员以随机的形式组成联盟,以构建联盟的成员地位平等,而实际情况是联盟成员重要性不同,发挥的作用不同,因此应用夏普利值方法需要衡量联盟成员的重要性。
确定联盟成员重要性评价指标需要考察构建战略联盟的目的。战略联盟的组建是为了提升物流企业的核心竞争力,提高企业效益。核心竞争力理论认为,有机整合性是核心竞争力的典型特征[7],并且企业是否能够在行业细分市场上具备核心竞争力,企业的变性特征占有主导作用。而企业的变性特征依赖于规模和范围经济、专利技术、渠道控制等管理与技能[8]。物流企业核心竞争力主要体现在一方面物流企业能否拥有成规模的客户群,为客户创造价值;另一方面物流企业能否在技术和资产方面占有优势[9]。对战略联盟形成动机的实证研究发现,我国企业组建战略联盟居前两位的动机是:寻求规模效益和综合利用资源[10]。可见,构建战略联盟主要在于提高企业规模经济性,提升企业在生产和管理中整合资源的能力。
通过对行业内资深专家调查发现,要提高企业规模经济性和整合能力,还需要企业具有良好的资金运作能力。同时,本文也考虑了指标实用性和简明性[11],采用了三个指标评价联盟成员重要性,即规模经济、技术先进、资金运作。
采用层次分析法确定不同成员重要性。层次分析法要求,建立三层分析框架:目标层、准则层和方案层。目标层指的是评价的目的,也就是联盟成员重要性,准则层则是评价重要性的三个指标,方案层是指需要评价的三个企业。
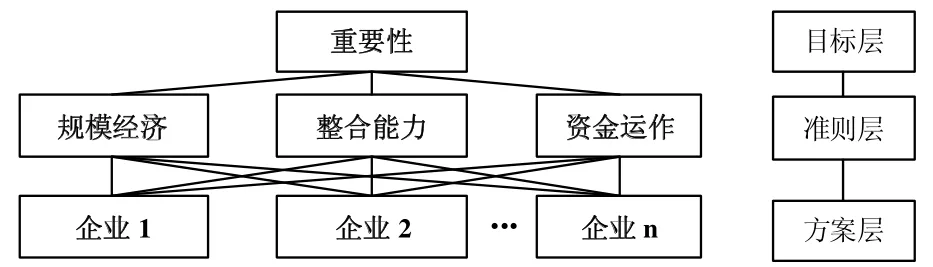
图1 联盟企业重要性分析框架
然后,对三个指标以及方案层各企业相对重要性进行排序打分。Saaty等人使用3,5,…17等27种分制对若干实例构造比较距阵,算出权向量,与实际对比发现,9分制较优。因此,本文也采用9分制。表1说明了不同分数的含义。
再者,建立比较矩阵分析,确定联盟成员的重要性权重 αI,(I=1,2,…, N)。根据夏普利值方法确定的联盟成员利益分配比例,结合重要性权重αI形成综合权重βI。最后,采用综合权重分配联盟利益。

表1 分数含义
2 实例分析
A,B,C三企业结成战略联盟,三家企业合作能够获取收益800万元。在每家企业单独经营情况下,收益分别为100万元,130万元和150万元,如果合作可获取收益350万元,其它情况任何两家合作均可获取300万元收益,则三家企业形成联盟博弈。
2.1 计算夏普利值

表2 A企业夏普利值推算表
N≜{1,2,3},i=1,2,3,分别代表A,B和C。v(φ)=0,v(1)= 100,v(2)=130,v(3)=150,v(1,3) =350,v(1,2)=300,v(2,3)= 300,v(1,2,3)=800。计算企业的夏普利值:

同样,计算φ2[]=251.7(万元),φ3[v]=286.7(万元)。分配比例为32.7%,31.5%,35.8%。
2.2 确定重要性权重
计算准则层权重,如表3所示。
三家企业规模经济,整合能力和资金运作的权重计算,

表3 准则层权重计算表
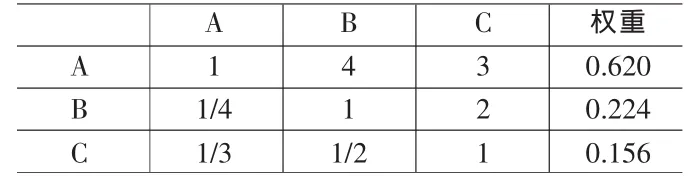
表4 规模经济权重计算表

表5 整合能力权重计算表
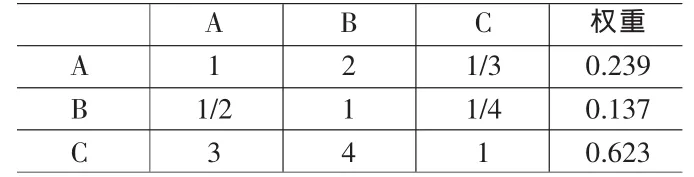
表6 资金运作权重计算表
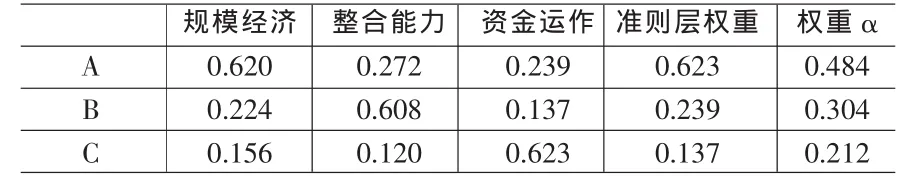
表7 重要性权重计算表
如表4~6所示。
确定重要性权重,如表7。
2.3 综合权重计算
将夏普利值的利益分配比例 (32.7%,31.5%,35.8%)与重要性权重αi(0.484,0.304,0.212)合并,得到综合权重(β1,β2, β3)=(0.480,0.290,0.230)。重新分配利益为383.8(万元),232.2(万元),184.0(万元)。
对比夏普利值法分配结果,本文认为,可利用层次分析法分析联盟成员重要性,并构建综合权重以改进夏普利值分配方法,重新分配联盟利益:
(1)可以保证夏普利值法的分配原则,即联盟总收益增加同时,各成员企业收益增加;
(2)联盟中相对重要的企业获取的利益高于单纯夏普利值分配结果,充分肯定了不同企业在联盟中的价值;
(3)说明了分配方案更加合理。
3 结论
针对物流企业战略联盟中的利益分配问题,本文提出以联盟博弈的夏普利值方法为基础,针对夏普利值方法的缺点,提出了联盟成员重要性评价指标;通过层次分析法对夏普利值进行改进,建立了新型联盟成员权重构建模型,从而对物流战略联盟利益进行重新分配。采用这种分配机制,不仅能够保证单纯夏普利值方法的分配原则,而且充分体现联盟企业在联盟中的重要性,使得利益分配更加合理。
[1]Farok J.Contractor,Wonchan Ra.Negotiating Alliance Contracts Strategy and Behavioral Effects of Alternative Compensation Arrangements[J].International Business Review.2000,(9).
[2]文科,朱延平.供应链成员企业相关利益分配研究[J].商业研究,2010,(1).
[3]庆艳华.供应链企业合作及其利益分配问题研究[D].中国优秀博硕士学位论文全文数据库,2006.
[4]Hart S,Mas-Colell A.Potential,Value,and Consistency[J].Econometrica,1987,55.
[5]Kalai E.Samet D.Monotonic Solutions to General Co operative Games[J].,Econometrica,1985,53(2).
[6]Marko Slikker.Note Coalition Formation and Potential Games[J]. Games and Economic Behavior,2001,(37).
[7]C.K.Prahalad,Gary Hamel.The Core Competence of the Corporation[J].Harvard Business Review,1990,(5~6).
[8]张石森,欧阳云主编.哈佛MBA核心竞争力全书[M].呼和浩特:远方出版社,2003.
[9]静涛.物流企业核心竞争力分析[J].科技信息,2010,(11).
[10]唐建民.物流联盟协同实现机制实证研究[J].学术论坛,2009,(10).
[11]程乾生.属性集和属性综合评价系统,系统工程理论与实践[J]. 1997,(9).
