基于改进背景值算法的优化GM(1,1)模型及其应用

毛文晋，冉 璐

（1.西南石油大学 经济管理学院，成都 610500；2.重庆三峡学院，重庆 万州 404000）

0 引言

由于GM(1,1)模型能用较少的数据序列建立模型去反映系统的主要动态特性，在显著不确定性和缺乏数据信息的领域得到了成功的应用,但同时也存在一些预测偏差过大的情况,反映了GM(1,1)模型的实用性有待提高[1][2]。在研究和应用灰色系统模型过程中，GM(1,1)模型的缺陷不断被发现，模型的不足之处不改进[3～10]。文献[3]提出预测公式中的以x(0)(1)为已知条件不合理；文献[4]指出灰微分方程参数方程组病态的问题；文献[5～10]指出导致GM(1,1)模型误差偏大的原因是该模型中背景值的构造方法不当所致，并给出了各自的改进方法。

而其中背景值的构造方法成为影响GM(1,1)模型精度和适应性的关键因素。实验结果显示，文献[9]的背景值构造方法具有更高的精度，同时既适用于低增长指数的数据列进行GM(1,1)预测，也适用于高增长指数的数据列进行GM(1,1)预测。但该文献中推导背景值计算公式时，假定，此与GM(1,1)预测公式相比少了常数项，导致在增长指数较小时反而不如传统GM(1,1)的拟合精度高。本文拟在文献[9]的基础上，重新推导背景值的计算公式；同时，考虑到最优的拟合曲线不一定经过历史数据中的某一点，利用误差最小的方法求解得到预测公式中最优C值。

1 改进背景值计算的GM(1,1)模型

x(1)序列满足下述一阶线性微分方程模型：

其中a为发展系数（增长指数），反映了数据序列x(1)及原始数据序列x(0)的发展趋势；u为灰作用量。其解为：

并称（1）式为（3）式的白化方程。

其中z(1)(k)为背景值，一般z(1)(k)=0.5x(1)(k-1)+0.5x(1)(k)(k= 2,3,…,n)。采用最小二乘算法求解估计a和u，可得：

其中

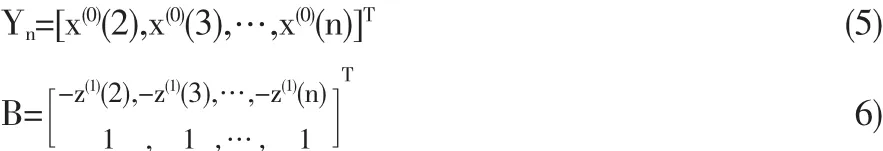
在区间[k-1,k]上对（1）式两边同时求积分可得：

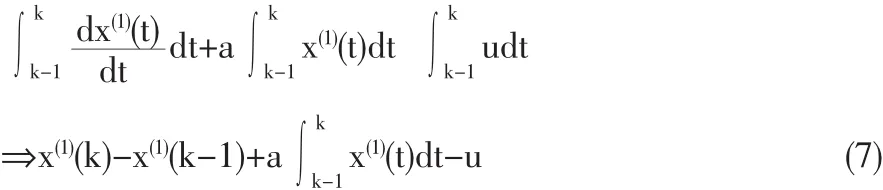
已知x(1)(u)-x(1)(u-1)=x(0)(u)，比较（3）式和（7）式可知应满足：

不妨假定x(1)(t)=CeAt+B，而x(0)(t)=ceait，离散化有：

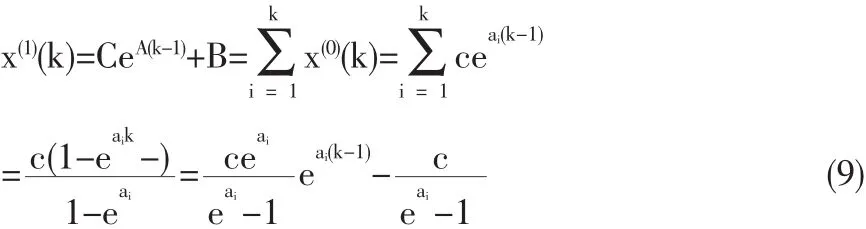
比较可得：

把x(1)(t)=CeAt+B带入（8）式，可得：

可见关键是确定A和B，由前定义可得：

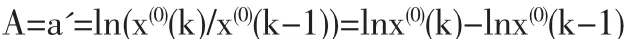
又因x(0)(1)=CeA(1-1)+B=C+B

则可求得：

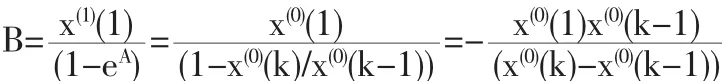
故可得新的背景值计算公式为：

基于新的背景值计算公式并由（4）式求解得到a和u，并代入（2）式并离散化，假定(k)代表原始累加数据x(1)(k)的预测值，则有：

在传统GM(1,1)预测公式中：

累减生成还原得到原始数据序列的灰色预测模型为：

2 优化初始值G

考虑到最优的拟合曲线不一定经过历史数据中的某一点，基于（16）式选择的初始值G不一定是最优的，即G的选取是影响GM(1,1)模型建模精度的又一个重要因素.为了获得最优的拟合曲线,提高模型的建模精度,需要对G进行优化。

定义：

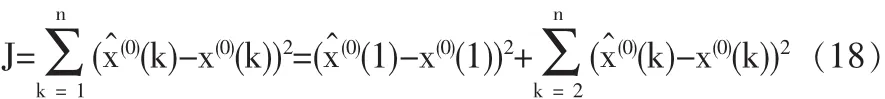
把（17）式代入（18）式可得：

求满足拟合值和原始值平方和误差最小的得：

简化后可得最有的G值为：

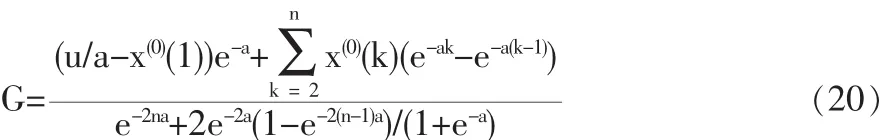
3 预测步骤和实例应用

3.1 预测步骤

由上面分析可总结预测步骤如下：

（1）由原始数据生成x(1)(k)，基于(13)式计算z(1)(k)，并基于(5)(6)式生成Yn和Bn；

（2）基于(4)式计算发展系数a和灰作用量u；

3.2 实例及应用

3.2.1 实例

为使结果有可比性，采用与文献[9]中相似的数据x(0)(k)-ea(k-1)(k=0,1,2,3,4,5)来建模预测，其中-a=0.05,1.5,2.5。把文献[9]中所提出模型称为模型[9]，本文模型称为新模型。由于在文献[9]中已经证明了模型[9]比其它改进背景值方法的模型有效，所以不在选用其它模型分析。但是，在-a=0.05时，model[9]的拟合和预测误差比传统的GM(1,1)模型（称为原模型）大，也采用了传统模型进行了分析和比较。定义残差ξ(k)为：

拟合和预测结果见表1～4。表1的结果表明传统GM (1,1)模型的结果比文献[9]模型的结果精度高，其原因在于模型[9]中忽略的常量在发展系数小时较大，不考虑就带来了较大误差。但是从表1～4可见，不关发展系数小（-a=0.05）还是大（-a=2.5），新模型的预测和拟合结果的精度都远高于另外两种模型，显示了其有效性。

3.2.2 应用

为进一步验证本文的算法，选用了文献[8]中的英国市场研究机构Analysys Ltd的一份研究报告预计的2004～2008年欧洲手机游戏市场规模进行了仿真建模分析。

定义相对误差为：

拟合结果见表5，从表中可见，当采用平均残差作为模型精度判断依据时，原模型、模型[9]、新模型的平均残差分别为0.4674、0.0993和0.0826，即新模型最好。

表1 -a=0.05时三种模型的拟合结果

表2 -a=1.5时模型[9]和新模型的拟合结果

表3 -a=2.5时模型[9]和新模型的拟合结果

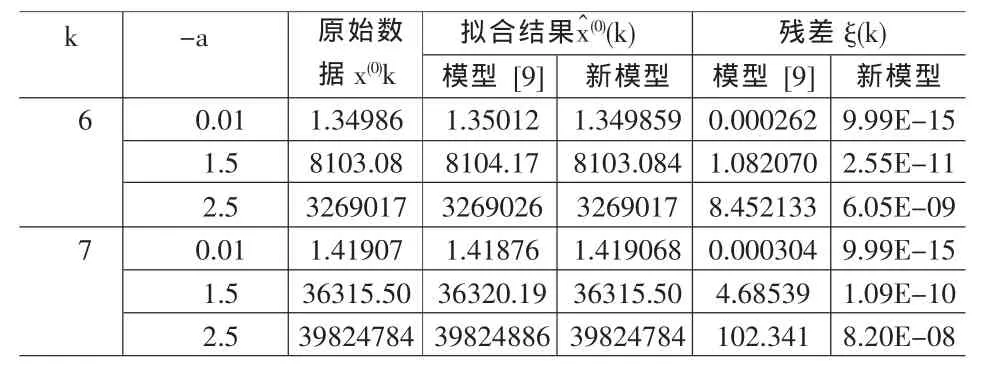
表4 -a=0.05,1.5,2.5和k=6,7时模型 [9]和新模型的预测结果

当采用平均相对误差作为模型精度判断依据时，原模型、模型 [9]、新模型的平均相对误差分别为 2.3743%、1.2113%和0.8697%，新模型最好。

当采用相对误差最大值作为模型精度判断依据时，原模型、模型 [9]、新模型的相对误差最大值分别为3.9801%、3.9909% 和1.8983%，也是新模型最好。本实例应用同样显示出了新模型的有效性。

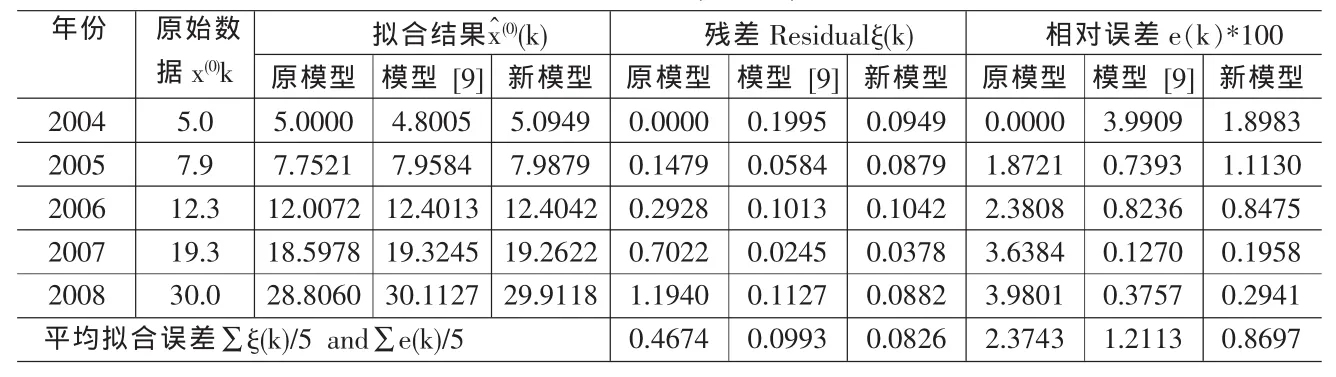
表5 三种模型的拟合结果(亿欧元)

4 结论

本文分析了GM(1,1)模型背景值的构造方法，并基于文献[9]提出了一种改进的构造计算方法。并对GM(1,1)模型的初始条件进行了优化，利用误差平方和最小的方法求解得到了其最优值，从而摆脱了原有模型的初始值经过了历史数据中的某一点的束缚。同时，相较传统GM(1,1)模型建模方法，本文提出的优化模型并没有变复杂，同时也继承了灰色模型所需历史数据少的优点，实现和计算简单。从实例模拟及分析可见，本文提出的优化GM(1,1)模型使得拟合、预测精度更高，适合范围宽。本文的研究具有一定的理论意义和应用价值。

[1]Yi Lin,Sifeng Liu.A Systemic Analysis with Data(I)[J].International Journal of General Systems(UK),2000,29(6).

[2]Fang Mei Tseng,Hsiao Cheng Yu,Gwo Hsiung Tzeng.Applied Hybrid Grey Model to Forecast Seasonal Time Series[J].Technological Forecasting and Social Change,2001,67.

[3]党耀国,刘思峰,刘斌.以x(1)(n)为初始条件的GM模型[J].中国管理科学,2005,13(1).

[4]张大海,江世芳,史开泉.灰色预测公式的理论缺陷及改进[J].系统工程理论与实践,2002,22(8).

[5]谭冠军.GM(1,1)模型的背景值构造方法和应用(I)[J].系统工程理论与实践,2000,20(4).

[6]李俊峰,戴文战,基于插值和Newton-Cores公式的GM(1,1)模型的背景值构造新方法与应用[J].系统工程理论与实践,2004,24 (10）.

[7]王义闹,刘光珍,刘开第.GM(1,1)的一种逐步优化直接建模方法[J].系统工程理论与实践,2000,20(9).

[8]张怡,魏勇,熊常伟.灰色模型GM(1,1)的一种新优化方法[J].系统工程理论与实践,2007,27(4).

[9]廖飞.对背景值优化的新 GM(1,1)模型[J].数学的实践与认识, 2009,39(18).

[10]罗党,刘思峰,党耀国.灰色模型GM(1,1)优化[J].中国工程科学, 2003,5(8).