一种社会经济系统模糊C划分聚类数的确定方法
2011-03-09钟映竑
贺 勇,钟映竑
(广东工业大学 管理学院,广州 510520)
0 引言
在社会经济系统建模与分析中,需要进行系统分解,即目标系统要划分为若干个子系统。这会面临两个问题:第一,如何划分;第二,划分多少个子系统。这实质上是一个聚类问题,涉及到聚类算法的选取和聚类数的确定。模糊C均值(Fuzzy C-Mean,FCM)聚类算法[1,2]作为无监督数据分类和分析的一个重要工具,已成功地用于模式识别及系统建模等领域。社会经济系统是个边界不明晰的软系统,相对于层次聚类法和快速聚类法等而言,模糊C均值划分更加适合处理此类系统,且可以获得更加丰富的知识。但FCM算法必须事先给定聚类数,在未知情况下,一般通过聚类有效性函数可来确定,而已提出的聚类有效性函数众多,不同的聚类有效性函数往往得到不同的聚类数。聚类有效性函数可分为两类:一类是以Bezdek的vPC[3]和vPE[4]为代表的基于数据集模糊划分的观点;另一类基于数据集的几何结构,以Xie和 Beni的vXB[5],Fukuyama和 Sugeno的 vFS[6]及Kwon的vk[7]为代表。然而,对于UCI上的标准数据集,没有一个有效性函数能保证都得到正确的分类数。这样,在现实的复杂经济系统中,将目标系统采用模糊C均值划分为若干个子系统时,应当选取哪个有效性函数没有任何根据,其最佳聚类数难以确定。
在现实目标系统中,如果仅仅依靠某个聚类有效性函数来确定聚类数,其结果可能并不理想,应当引入专家经验。可以这么认为,一个好的聚类应该满足:其一,其聚类数合理,符合解决问题的需要,这需要通过专家经验来判断;其二,聚类结果科学、可信,需要通过经典的聚类有效性函数来检验。将专家知识和科学计算结合起来,针对社会经济系统,本文将提出一种模糊软划分聚类数的确定方法,主要步骤是:首先进行数据分析,几何结构上,观察数据集是否可聚;其次,专家根据问题给出聚类数集合;最后,对可供选择的每一个聚类数,采用聚类有效性函数集来评价,满足有效性函数最多的聚类数被认定为最佳聚类数。
1 分类指标的选取
若实际产出为Y,有n个投入要素,则生产函数的一般形式为[8]:

它代表产出与投入要素之间的某种依存关系。为了实现对广东省21个地区的科技进步水平进行软分类,遵循柯布-道格拉斯(C.W.Cobb-D.H.Douglas)[9]:

式中α、β是常数,K,L分别代表资本投入、劳动投入,A代表技术进步水平。从(2)式得到:

式(3)表示一个地区的技术进步与该地区的产出、资本投入、劳动投入具有一定的依存关系。基于这种关系,这里科技进步人均产出、固定资产投入和人力资本来反映,根据2001~2009广东省统计年鉴相关数据进行处理得到人均GDP(单位:万元)、人均固定资产(单位:万元)及人力资本数据(计算方法详见文献10),得到表1。

表1 各地区指标值
2 分类数的确定
对聚类有效性函数的研究可分为两类:一类是基于模糊划分的方法,认为好的聚类对应于数据集是较分明、较明晰的,代表函数如Bezdek提出的分割系数vPC和分割熵vPE;另一类是基于几何结构的方法,认为每个子类应当是紧致的,子类与子类相互间尽可能分离,代表函数有Xie和Beni的vXB,Fukuyama和Sugeno的vFS,Kwon的vK等。上面提到的5个有效性函数如表2所示。在评价聚类结果时,这5个有效性函数并不一定同时达到最优。可以这样认为:多个有效性函数取得最优值的聚类结果为较优的结果,该结果对应的聚类个数为最佳的聚类数。

表2 聚类有效性函数
从图1中,我们可看到21个地区固定资产、人力资本和GDP构成的三维数据散点图,可看出待分析的数据是存在聚类趋势的,具有可聚性[11]。由散点图及实际研究问题的需要,我们将聚类数区间定为c={2,3,4,5,6}。在不同类别下,5个有效性函数值都在时达到最优。由此我们可得出结论:2000~ 2008年期间广东省各地区按科技水平划分的最佳类别数为3类。
3 分类结果及分析

图1 21个地区数据散点图
设定分类数为3,对广东省21个地区按技术进步水平进行软划分,即对三维向量集{(Yt,Kt,Lt)}模糊分类,结果如表3及图2所示。

表3 科技进步水平分类表
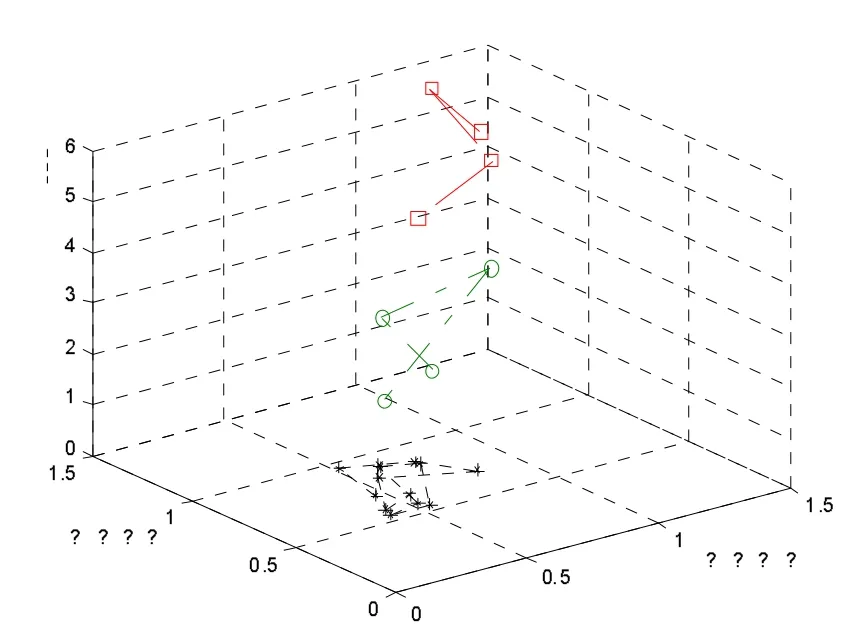
图2 分类结果

表4 类中心矢量
可见,分类结果比较好地反映了广东省的经济发展情况。事实上,第一类包含两个广州、深圳两个副省级城市、珠海特区及经济重地佛山,是珠三角的龙头,科技进步水平最高;第二类均为珠三角城市,区位优势突出,经济发展潜力巨大;第三类主要是东西两翼及粤北地区,虽然这些地区之间以及各个地区内部的科技进步有明显差异,但它们都具有农业人口比重大,贫困人口多,科技进步水平整体上偏低。表4列出的是各类的类中心矢量(均为归一化后数据),表5列出的是各个地区属于各类的程度。
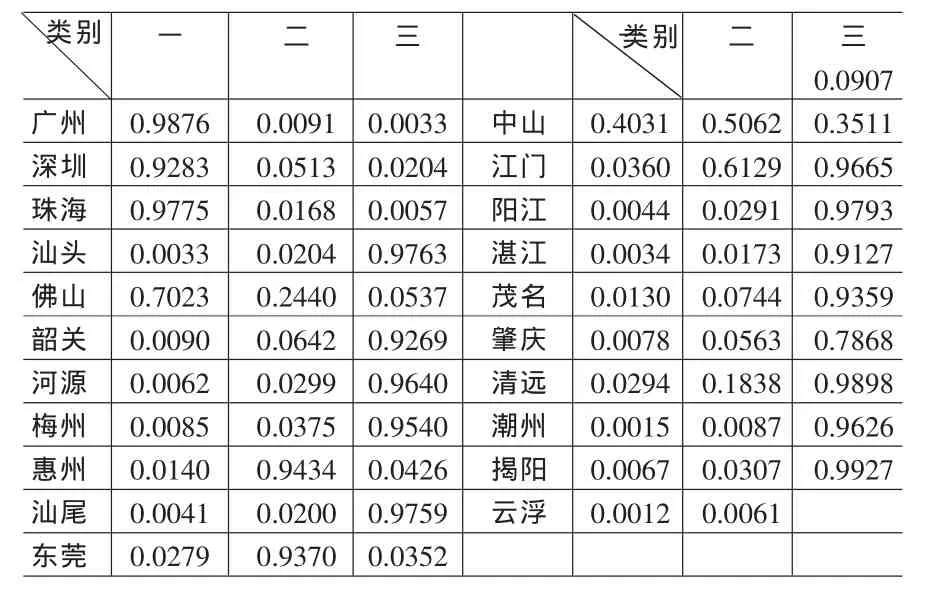
表5 隶属度表
从隶属度矩阵(表 5)发现:广州属于第一类的程度是0.9876,而佛山是0.7023,表明虽然它们的科技进步水平可以认为属于同一类,但广州的科技进步水平高于佛山。中山属于第一类及第二类的程度分别0.4031和0.5062,相对比较划归第二类;而江门属于第二类及第三类的程度分别是0.6129和0.3511,相对比较划归第二类,但是属于第一类程度仅为0.0360,说明尽管中山、江门同属第二类,但中山科技水平要比江门高。第三类地区属于第三类的隶属度均超过0.7以上,都划归第三类。可见表3是科技进步的粗分类,而表5正好反映的是每一类中更细致的划分。两个表综合反映了广东省各地区科技进步水平的分类,符合广东省的实际情况。
4 结论
在对社会经济系统进行聚类时,应将专家知识和科学计算相结合。一个好的聚类应不仅符合客观现实,即聚类数合理,而且应尽量满足经典的聚类有效性函数,即聚类结果科学。本文在给定合理可行的聚类数集合的基础上,采用多个聚类有效性函数对对各个聚类数进行优选的方法,以科技进步水平对广东省21个地区进行了划分:首先,确定衡量科技进步水平的数据集;进而对数据集进行分析,判断是否具有聚类趋势;然后采用所提出方法进行聚类,得到了满意的聚类数及聚类结果。研究显示,广东省按科技进步水平应分为3类,分类结果符合实际。
[1]Dunn J.C.Some Recent Investigations of a New Fuzzy Partition Algorithm and Its Application to Pattern Classification Problems [J].J.Cybernetics,1974,(4).
[2]Bezdek,J.C.Pattern Recognition with Fuzzy Objective Function Algorithm[M].NY:Plenum Press,1981.
[3]Bezdek J.C.Cluster Validity with Fuzzy Sets[J].J.Cybernetics,1974,3(3).
[4]Bezdek J.C.Mathematical Models for Systematic and Taxonomy [C].In:Proceedings of 8th International Conference on Numerical Taxonomy,San Francisco,1975.
[5]Xie X.L,Beni,G.A.Validity Measure for Fuzzy Clustering[J]. IEEE Trans.Pattern Anal.Machine Intell,1991,3(8).
[6]Fukuyama Y.,Sugeno,M.A New Method of Choosing the Number of Clusters for the Fuzzy C-means Method[C].In:Proceedings of 5th Fuzzy System Symposium,.1989.
[7]S.H.Kwon.Cluster Validity Index for Fuzzy Clustering[J].Electron.Lett.,1998,34(22).
[8]Solow.R.M.A Contribution to the Theory of Economic Growth [J].Quarterly Journal of Economics,1956,39(1).
[9]Rome.P.Endogenous Technological Change[J].Journal of Political Economy,1990,98(5).
[10]贺勇,诸克军.基于软计算的生产要素对地区经济影响分析[J].系统管理学报,2009,18(3).
[11]高新波.模糊聚类分析及其应用[M].西安:西安电子科技大学出版社,2004.
