概率积分法参数对预计地表下沉的影响度分析
2011-03-08米丽倩查剑锋刘丙方
米丽倩,查剑锋,刘丙方
(1.中国矿业大学,江苏徐州 221116;2.江苏省资源环境信息工程重点实验室,江苏徐州 221116; 3.国土环境与灾害监测国家测绘局重点实验室,江苏徐州 221116;4.兖州煤业股份公司南屯煤矿,山东邹城 273515)
概率积分法参数对预计地表下沉的影响度分析
米丽倩1,2,3,查剑锋2,刘丙方4
(1.中国矿业大学,江苏徐州 221116;2.江苏省资源环境信息工程重点实验室,江苏徐州 221116; 3.国土环境与灾害监测国家测绘局重点实验室,江苏徐州 221116;4.兖州煤业股份公司南屯煤矿,山东邹城 273515)
地表沉陷预计的常用算法——概率积分法的预计参数及参数间交互作用对变形值不同的影响程度,造成参数选取、反演的不确定性。针对这一问题,采用五元二次正交旋转组合设计,研究了概率积分法中预计参数对地表点最大下沉的影响关系,得出了单因素与两两因素交互作用对地表点最大下沉值的影响规律。研究结果表明:沉陷预计参数中的下沉系数、主要影响角正切、拐点偏移距对预计最大下沉具有显著影响,影响程度排序为:下沉系数>主要影响角正切>拐点偏移距;且q与tanβ、tanβ与S/H的交互作用影响明显。
概率积分法参数;开采沉陷;最大下沉值;二次正交旋转组合设计
下沉系数q、水平移动系数b、主要影响角正切tanβ、拐点偏移距S、影响传播角θ,是概率积分法模型的主要预计参数。根据地表移动监测站实测数据反演是获取这些参数的主要方法,由于参数之间的相关性,使得反演结果过度依赖初值,且反演结果不惟一,造成使用过程中的困难。针对这一问题,采用试验设计方法研究了概率积分法参数对预计结果的影响度,并分析了各因素之间相关性。
开采沉陷稳定后,地表最大下沉值及其他移动变形值能从整体上反映地表变形的剧烈程度,而最大下沉值又是所有其他变量的决定参量之一[1]。因此,将最大下沉值作为影响度指标来评价各参数对变形值的影响程度。本文采用二次正交旋转组合设计建立了各因素与最大下沉值的回归模型,并分析了各参数及其交互作用对最大下沉值的影响规律,对概率积分法参数选取和反演具有指导意义。
1 概率积分法模型基本原理
概率积分法是因其所用的移动和变形预计公式中含有概率积分 (或其导数)而得名,由于这种方法的基础是随机介质理论,所以又叫随机介质理论法[2]。
1.1 最大下沉值计算基本方程
充分采动条件下最大下沉值为

式中,q为下沉系数;m为煤层的开采厚度,m;α为煤层倾角,(°)。
实际上,大多数情况下地表沉陷预计区域为非充分采动区域,此时按照概率积分法理论,可将其视为两个半无限开采的叠加,不失一般性。
倾斜煤层开采中半无限开采时,单元 [坐标为 (s,t)]的开采引起地表任意点[坐标为 (x,y)]的下沉值为:

式中,r为主要影响半径,r=H/tanβ;H为采深。

有限开采时煤层的开采等效于两个半无限开采的几何叠加,地表下沉值计算公式为:
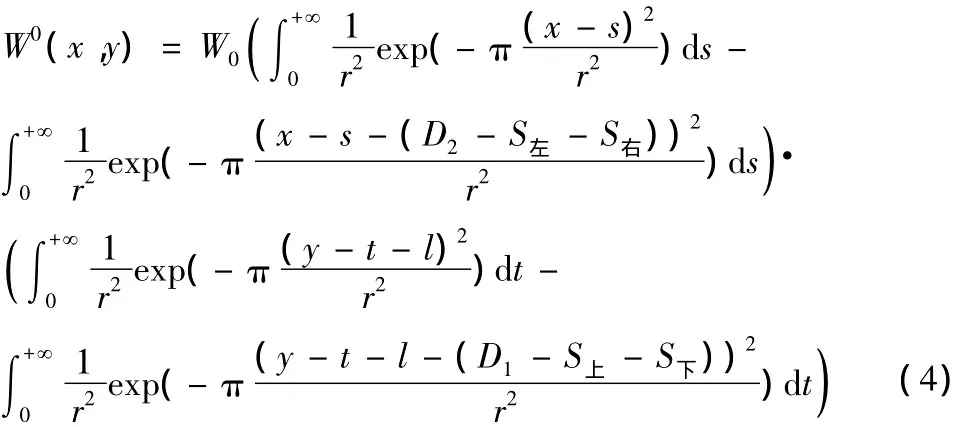
式中,D1,D2分别为工作面倾向长和走向长;S上,S下,S左,S右为上、下、左、右边界的拐点偏距。
1.2 参数影响的理论分析
由上述公式可知,W与q始终呈线性关系; tanβ与S/H参与运算较多,且变化范围较大,故其变化可能会引起下沉值的较大改变,所以3个参数对下沉值的影响应该较为显著。而q,tanβ,S/ H的变化都会引起地表移动盆地边界和面积的改变,故3个参数之间可能具有交互作用,但从繁杂的计算公式中难以准确观察出3个参数及其交互作用对下沉值的具体影响程度。计算公式中参数b不参与运算,可知b的变化对最大下沉值无影响。θ是倾向主断面预计特有的参数,θ的变化使下沉盆地和倾斜方向上的拐点位置都产生一定的偏移,因此,当θ的变化不改变移动盆地采动的充分性或非充分性时,其只改变倾向主断面上的最大下沉值位置,对其数值无影响;但当θ的变化改变移动盆地的采动程度时,将会使最大下沉值产生变化,由于θ的变化范围较小,其对下沉值的影响甚微。
2 试验方案
二次正交旋转组合设计是正交试验设计的一种,其既能分析处理单因素及因子间交互作用对指标的影响,又能建立定量的数学模型,属于更高级的试验设计技术[3-4]。采用五因素五水平的试验,根据二次正交旋转组合设计的原则,仅需36次试验就能全面分析各单因子及因子间的交互作用对最大下沉值的影响。
模拟试验区的地质采矿条件如图1所示,若采厚m=3m,工作面倾向长D1=400m,走向长D2= 400m,下边界采深H1=450m,上边界采深H2= 350m,已知地面标高为30m。
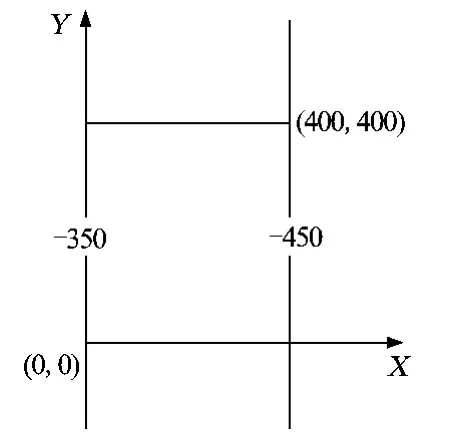
图1 工作面采矿条件
试验因素选取为q—X1,b—X2,tanβ—X3,S/H—X4,θ—X5,试验指标为最大下沉值W(mm)。采用二次正交旋转组合设计进行试验,因素水平编码如表1所示。

表1 因素水平编码

表2 试验方案及结果
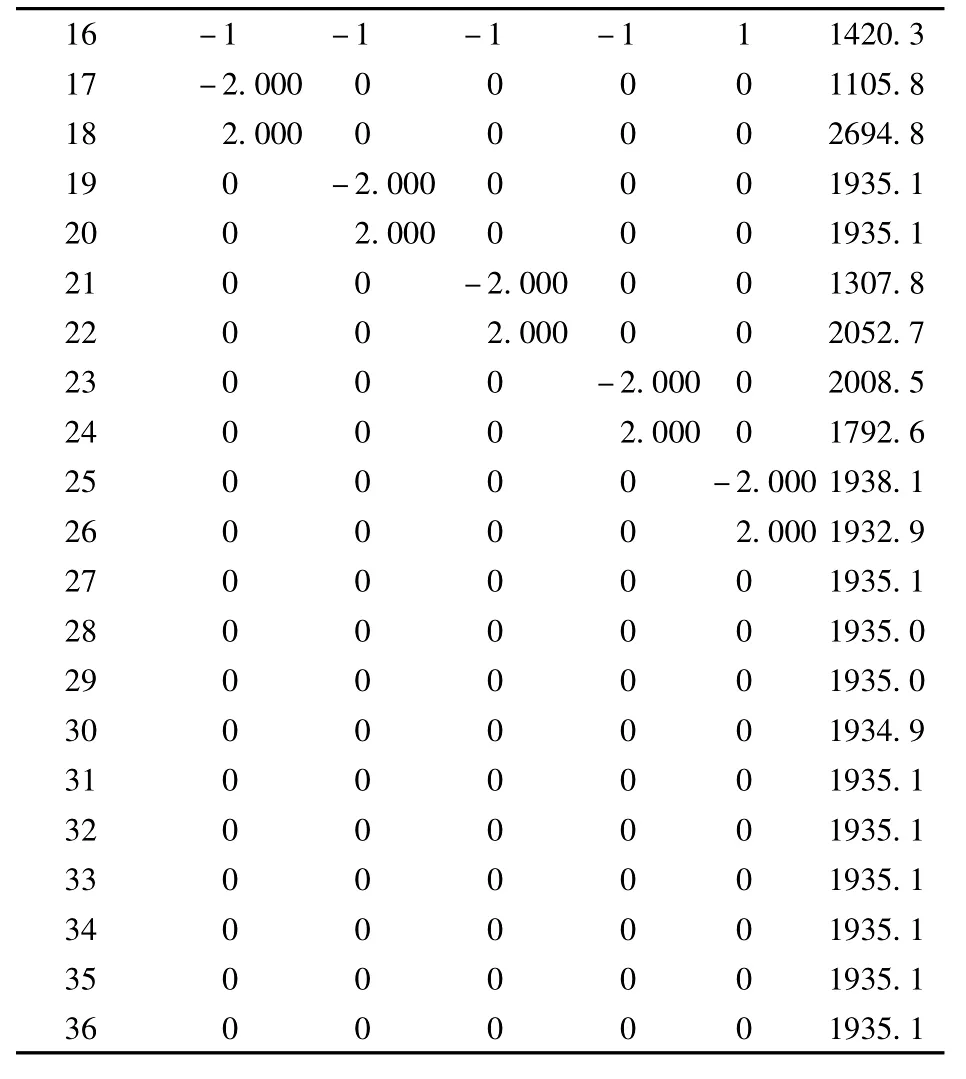
表2 试验方案及结果(续)
3 试验结果分析
3.1 数学模型的建立
利用DPS[5]软件处理试验数据,得到试验因素对最大下沉值的影响分析表,如表3所示。

表3 试验结果方差分析
由表3可得,因素X1,X3,X4,1X3,X3X4极显著,各因素与最大下沉值之间的回归模型为:

3.2 主因子效应分析
由表3中F值可知,影响最大下沉值的各因素的主次顺序依次为q,tanβ,S/H,θ,b。分别将回归模型 (5)中的4个因素固定在零水平,另一因素固定在-2,-1,0,1,2五个水平,得到单因素对最大下沉值影响的变化曲线 (见图2)。

图2 主因子效应
由图2可知,X1与W的关系曲线为直线,W随着X1的增加而增大;X3与W的关系曲线为抛物线,在[-2.0,1.3]水平区域内,随着X3水平的增加,W随之增大,X3在1.3水平,W达到最大值;在[1.3,2.0]水平区域内,随着X3水平的增加,W随之减小;X4与W的关系曲线为抛物线,随着X4水平的增加,W随之减小;X5与W的关系曲线为近似与X轴平行的直线,说明θ的变化对W基本无影响。X2与W的关系为与X轴平行的直线,说明b对W无影响。
3.3 两因素交互作用分析
从回归系数的绝对值可以看出,各因子间交互作用对最大下沉值的影响大小依次为:X3X4>X1X3>X1X4>X2X5>X1X5>X1X2>X4X5>X3X5>X2X3>X2X4。从回归系数显著性检验可看出,q与tanβ,tanβ与S/H的交互作用对最大下沉值的影响明显,且tanβ与S/H的交互作用大于q与tanβ的交互作用。
将X2,X4,X5固定在零水平,得到X1,X3两因素交互作用对最大下沉值的影响模型为:

通过MATLAB的图形绘制工具[6],得到X1,X3两因素交互作用对最大下沉值影响的响应曲面图,如图3。

图3 q和tanβ对最大下沉值的影响
由图3可知:当X3(tanβ)一定时,随着X1(q)的增加,W逐渐增大;X1(q)一定时,随着X3(tanβ)的增加,W有一个先增大后减小的过程。但q对结果的影响更为显著,且当X1,X3都为-2,即q=0.40,tanβ=1.2时,W取得最小值。
同理将X1,X2,X5固定在零水平,得到X3,X4两因素交互作用对最大下沉值的影响模型为:
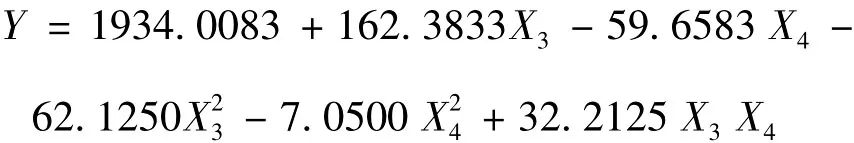
图4为X3,X4两因素交互作用对最大下沉值影响的响应曲面图。
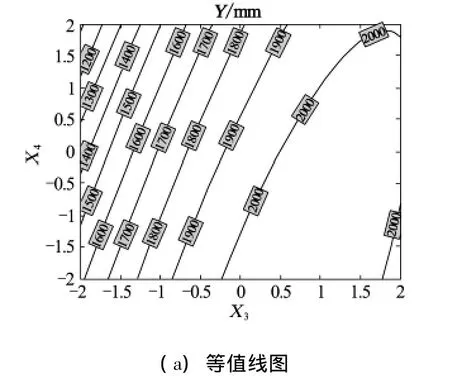
由图4可知,当X4(S/H)为定值时,随着X3(tanβ)的增加,W有一个先增大后减小的过程;当tanβ为定值时,随着S/H的增加,W逐渐减小。但tanβ对结果的影响更为显著。当X3在-2~-1,X4在1.5~2.0,即tanβ在1.2~1.65,S/H在0.17~0.20时,W值较小。

图4 tanβ和S/H对最大下沉值的影响
4 结论
(1)通过五元二次正交旋转组合设计试验,建立了q,b,tanβ,S/H,θ五因素对最大下沉值的影响模型。
(2)根据单因子及两因子交互作用分析表明,在试验范围内,得出5个因素对最大下沉值影响的显著性大小依次为q>tanβ>S/H>θ>b。q与tanβ,tanβ与S/H的交互作用对最大下沉值的影响明显,且tanβ与S/H的交互作用大于q与tanβ的交互作用。此结论与对概率积分法模型的理论分析结果相吻合。
(3)参数选取和参数反演的优化。应用概率积分法预计最大下沉值时,根据参数的影响度依次选择参数,抓住主要因素,忽略次要因素,提高预计的精度。由于q与tanβ,tanβ与S/H的交互作用对最大下沉值的影响明显,应用最大下沉值进行概率积分法参数反演时应将tanβ作为首要反演值,以减少反演时参数之间的相关性带来的反演结果的不确定性。
[1]邹友峰,邓喀中,马伟民,等.矿山开采沉陷工程[M].徐州:中国矿业大学出社,2003.
[2]何国清,等.矿山开采沉陷学[M].徐州:中国矿业大学出版社,1991.
[3]洪 伟,吴承祯.试验设计与分析—原理·操作·案例[M].北京:中国林业出版社,2004.
[4]茆诗松,周纪芗,陈 颖,等.试验设计[M].北京:中国统计出版社,2004.
[5]唐起义,冯光明,等.DPS数据处理系统:实验设计、统计分析及数据挖掘[M].北京:科学出版社,2007.
[6]周建兴,岂兴明,矫津益,等.MATLAB从入门到精通[M].北京:人民邮电出社,2008.
Analysis of Probability Integral Parameters'Influence on Predicting Surface Subsidence
MILi-qian1,2,3,ZHA Jian-feng2,LIU Bing-fang4
(1.China University of Mining&Technology,Xuzhou 221116,China;2.Jiangsu Provincial Key Laboratory of Resources Environment Information Engineering,Xuzhou 221116,China; 3.Land Environment and Disaster Monitoring Key Laboratory of State Survey Bureau of China,Xuzhou 221116,China; 4.Nantun Colliery,Yanzhou Coal Corporation,Zoucheng 273515,China)
Different influence degree of parameters of probability integralmethod for surface subsidence prediction and mutual action on deformation value would cause the uncertain problem of parameter selection and back-analysis.In order to solve the problem,this paper applied secondary orthogonal rotary combined design with 5 factors to researching influence of prediction parameters on surface maximum subsidence.Influence rule of single factor and random double factors on maximum subsidence was obtained.Results showed that subsidence ratio,tangent ofmain influence angle and inflexion offsetweremain influence factors ofmaximum subsidence.The influence degree was listed as:subsidence ratio>tangent of main influence angle>inflexion offset.Mutual influence of q and tanβ,tanβand S/H was evident.
mining subsidence;parameters of probability integralmethod;maximum subsidence value;secondary orthogonal rotary combined design
TD327
A
1006-6225(2011)04-0013-04
2011-03-31
国家自然科学基金重点项目 (50834004);地质灾害防治与地质环境保护国家重点实验室开放基金资助项目(SKLGP2010K002);国土环境与灾害监测国家测绘局重点实验室开放基金 (LEDM2009B01)
米丽倩 (1989-),女,山东聊城人,研究生,主要研究方向为开采沉陷预计,变形监测数据处理。
[责任编辑:徐乃忠]
