一种简化的AVL树的实现方法

刘绍翰 高天行 黄志球

(南京航空航天大学信息科学与技术学院,南京 210093)

平衡树是二叉查找树的一种,维持树的平衡可以避免二叉查找树的病态结构,减少查找路径的平均长度,降低查找的时间平均复杂度.自1962年第一种平衡树被发现至今[1],围绕着更简单的实现和更高的性能,提出了多种平衡树,不同平衡树的平衡调整策略往往不相同.最经典的平衡树是AVL树[1],加权平衡树[2]、替罪羊树[3]、伸展树[4]、随机平衡树[5]、秩平衡树等[6].AVL树的性能是最优二叉查找树与任意二叉树的折衷,平衡程度严格,查找的时间复杂度低,适用于删除插入操作较少的场合.

本文对AVL树的实现进行了分析研究:第1部分介绍了二叉查找树及AVL树的基本原理和操作;第2部分在分析AVL树的数学模型的基础上,给出了更为简洁的数学描述—HAVL树,包括定义、插入、删除、平衡等基本操作;最后进行了总结.

1 二叉查找树的基本性质与操作

一棵二叉查找树是按二叉树结构来组织的.其每个节点中至少含有3个域:key,left,right.其中key为关键字域,用于节点大小的比较;left和right用来存放指向左子树和右子树的指针.如果某个节点的子节点不存在,则该节点相应的指针域为NIL.二叉查找树中关键字的存储方式满足二叉查找树性质:设x为二叉查找树的一个节点,如果y是x的左子树中的一个节点,则key[y]≤key[x];如果y是x的右子树中的一个节点,则key[x]≤key[y].

一棵n个节点高度为h的二叉查找树的基本操作如下,如SEARCH(查找)、PREDECESSOR(前驱)、SUCCESSOR(后继)、MINIMUM(最小值)、MAXIM UN(最大值)、INSERT(插入)、DELETE(删除)、HAVL-MAINTAIN(维持平衡)和辅助ROTATE(旋转操作)等,其时间复杂度都为O(lgn).当树退化为线性结构时,其操作的时间复杂度就与链表相同,为O(n);而平衡二叉查找树通过旋转使二叉树在插入、删除等操作过程中保持子树的高度差相差不大,能保证在最坏情况下查找的时间复杂度为 O (lgn).

AVL的逻辑简单,易于理解,效率优秀.但是AVL实现较复杂,因为其用于平衡的附加域操作复杂,不易于更新,本文采用另一种“简单的”附加域—高度(Height)来代替通常用的平衡因子,用于控制二叉查找树的平衡,从而简化AVL的实现,简称它为HAVL(Height VAL).

2 HAVL树的性质与操作

高度的定义1:height用来存储以该节点为根的子树的高度.其中高度定义为:如果树是叶子节点,则其高度为1,否则节点t的定义如下: height[t]=max(height[left],height[right])+1 (1)“高度”相对于“高度差”是一种更简单的统计量,因为一个节点的高度可以仅由其左右子树的高度求得. AVL为每个节点增加一个域表示其左右子树的高度差,称为平衡因子,该因子可由高度求出.平衡因子取值范围是:-1,0或1,即0≤||height[right[t]]-height[left[t]]||≤1.按照左右子树的高度的不同可分为如下两种情况:

如果height[right[t]]-height[left[t]]≥0,有

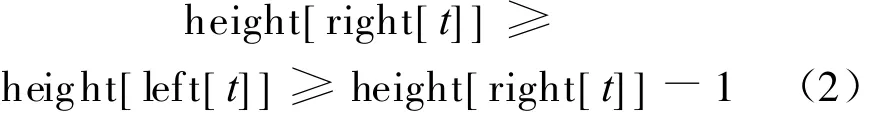
否则height[left[t]]-height[right[t]]≥0,有

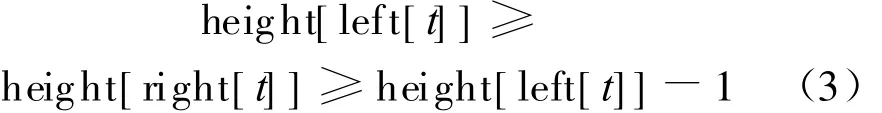
2.1 HAVL树定义

HAVL是二叉查找树,在每个节点上增加了一个域height存储以该节点为根的子树的高度.由定义1和公式(2)、(3),高度平衡树中的任意节点t满足两个条件之一:

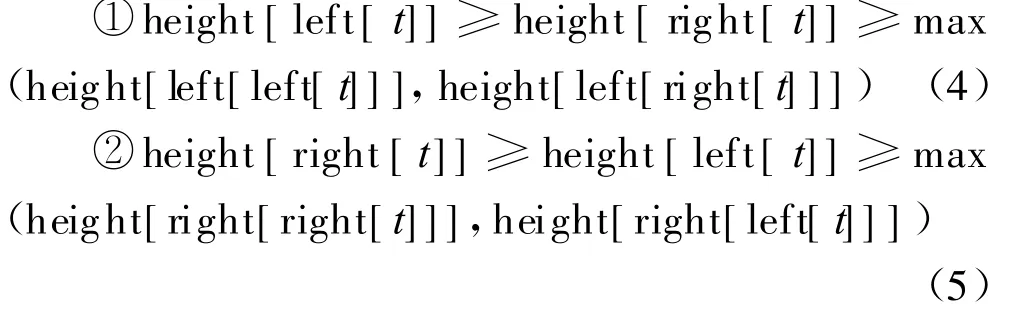
令height[left[t]]=max(height[left[left[t]]], height[left[right[t]]])+1代入公式(4),height [right[t]]=max(height[right[right[t]]],height [right[left[t]]])+1代入公式(5),可以立即得出平衡因子为1,0,-1的情况,该定义与AVL树的定义是等价的,但是HAVL树的实现不必按照平衡因子分情况讨论.

2.2 HAVL树的旋转操作

从定义1可以看出,节点的高度等于左右子树的高度取最大值加1,在旋转操作的同时可以维持节点的高度信息,从而使调用该函数的上层函数不必关心该域的计算,简化了实现方式.

维持平衡的左旋与右旋过程:在过程HAVLRIGHT-ROTATE中,假设left[x]≠NIL;HAVL -LEFT-ROTATE中,假设right[x]≠NIL.

2.3 HAVL树的平衡操作

过程HAVL-MAINTAIN实现对HAVL的子树的平衡.AVL树的不平衡情况有多种,都是经过合理的调整,按照平衡因子分为不同的旋转情况. HAVL树给出了它的简洁定义(公式(4)、(5)),从中可以看出,HAVL-MAINTAIN逻辑上与一般的AVL平衡过程等价,AVL树的实现需要按照不同的平衡因子分情况旋转并重新计算平衡因子[7],程序代码太长,而HAVL由于不必关心平衡因子取值的不同情况,过程相当简洁,实现简单,代码是一般AVL树实现方式的几分之一.

HAVL-MAINTAIN(t)

(1)if height[left[t]]＜height[right[t]]-1

(2)then if height[right[left[t]]]＜height[right[right [t]]]

(3)then HAVL-RIGHT-ROTATE(right[t])

(4)HAVL-LEFT-ROTA TE(t)

(5)return

(6)if height[right[t]]＜height[left[t]]-1

(7)then if height[left[right[t]]]＜height[left[left [t]]]

(8)then HAVL-LEFT-ROTATE(left[t])

(9)HAVL-RIGHT-ROTATE(t)

(10)return

2.4 HAVL树的插入操作

为了将一个新值v插入HAVL,可调用过程HAVL-INSERT.传递给该过程的参数是节点z,且有key[z]=v,left[z]=NIL,right[z]=NIL,height [z]=0.

HAVL-INSERT(t,z)

(1)if t=NIL then t←z return

(2)if key[z]≤key[t]

(3)then HAVL-INSERT(left[t],z)

(4)else HAVL-INSERT(right[t],z)

(5)height[t]←max(height[left[t]],height[right[t]]) +1

(6)HAVL-M AIN TAIN(t)

2.5 HAVL树的删除操作

过程HAVL-DELETE-MIN的功能是删除树中键值最小的节点,并返回被删除节点.

HAV L-DELETE-MIN(x)

(1)if left[x]=NIL

(2)then y←x

(3)x←right[x]

(4)return y

(5)y←HAVL-DELETE-MIN(left[x])

(6)height[x]←max(height[left[x]],height[right[x]]) +1

(7)HAVL-M AIN TAIN(x)

(8)return y

过程HAVL-DELETE-ROOT的功能是删除树的根节点,并返回被删除节点;过程HAVL-DELETE的功能是删除树中的键值为v的节点,并返回被删除节点.若节点不存在,无操作,返回NIL.

HAV L-DELETE-ROOT(x)

(1)if height[x]=1

(2)then y←x

(3)if left[x]=NIL

(4)then x←right[x]

(5)else x←left[x]

(6)return y

(7)y←HAVL-MIN(right[x])

(8)swap(key[y],key[x])

(9)HAVL-M AIN TAIN(x)

(10)return y

HAV L-DELETE(x,v)

(1)if x=NIL then return NIL

(2)if v=key[x]

then return HAVL-DELET E-ROOT(x)

(3)if v＜key[x]

(4)then y←HAVL-DELETE(left[x],v)

(5)else y←HAVL-DELETE(right[x],v)

(6)HAVL-M AIN TAIN(x)

(7)return y

3 实验结果比较

实验设置下:分别向完全为二叉树、AVL, HAVL,红黑树(RBT)树插入2000000个随机结点,分别计算其运行时间、树的高度、深度、旋转的次数.取20次实验的平均值结果并与完全二叉树进行比较,实验结果见表1.

平均深度反映了树的平衡程度,并且直接与查找性能成正比.表1中不同的平衡树的运行速度有明显的差异,HAVL因为程序设计更为紧凑,运行时间更短比AVL树更短,但是HAVL树与AVL树的平均路径长度、高度、深度和旋转次数是一样的,平均路径长度要好于RBT.由于RBT是不严格的平衡树,所需旋转的次数更少时间更快,少于 AVL树,但比HAVL树长.

表1 与主流平衡树的性能比较

4 总 结

本文论述了平衡二叉查找树附加域选择的灵活性和由此带来的实现上的简洁.这种简化能保持AVL树的特性,并且原理描述直观、程序实现简单,运行时间更短.

[1] Adelson-Velskii G M,Landis E M.An Algorithm for the Organization of Information[J].Soviet.Mat.Doklady,1962.

[2] Baer J L.Weight-balanced Trees[C].Proceedings of AFIPS 1975 NCC.,1975,44:467-472.

[3] Galperin,Rivest R.Scapegoat T rees[C].In Proceedings of the 4th Annual ACM-SIAM Symposium on Discrete Algorithms(SODA'93),1993:165-174.

[4] Sleator D D,Tarjan R E.Self-adjusting Binary Search Trees[J].JACM,1985,32:652-686.

[5] Bent S W,Driscoll J R.Randomly Balanced Search Trees[M].Manuscript,1991.

[6] Haeupler B,Sen S,Tarjan R E.Rank-Balanced Trees [C].11th International Workshop on Algorithms and Data Structures(WADS 2009),Aug 21-23,2009 Banff Canada.Algorithms and Data Structures,2009:351-362.

[7] 严蔚敏,吴伟民.数据结构[M].北京:清华大学出版社, 1997.