采用修正弦线模量法预测基础的非线性沉降
2011-03-07李仁平
李仁平 罗 勉
(三峡大学土木与建筑学院,湖北宜昌 443002)
现行浅基础设计方法分二步进行:一是确定地基的容许承载力(或地基承载力特征值)和极限承载力;二是根据基础受到的荷载验算地基的沉降.这种方法的缺点是将地基的承载力与沉降问题割裂开来;对于地基的沉降验算,则是假定地基的变形处于线弹性变形(小变形)阶段,按线弹性理论采用变形模量或压缩模量计算地基的沉降.实际上地基的变形是非线性的,即使在较小的荷载下,地基的变形也往往表现出明显的非线性,导致沉降计算结果的可靠性较差.
在基础尺寸、地基土层地质条件等因素已经确定的情况下,基础的荷载沉降曲线是唯一的,如果能够预先准确计算出基础的荷载沉降曲线,那么以沉降变形控制为目的的基础设计就是非常简单的事情.但现有的沉降分析方法却难以做到这一点.Briaud和Gibbens[1]在砂土地基中进行了一系列方形基础的加载试验,试验基础尺寸在1.0~3.0m之间,基础厚度为1.5m,埋深0.75m,地基持力层为均质的粉砂土,地下水位埋深4.9m.试验前对场地做了详细的勘察和原位测试工作.为了检验各种沉降预测方法的准确性,他们组织了一次国际研讨会,各参会成员根据基础尺寸、勘察数据及原位测试等资料预测不同尺寸基础在沉降等于25mm和150mm时需要的荷载Q25及Q150,以及基础在荷载Q25作用30min和20年后发生的蠕变沉降增量.来自以色列、澳大利亚、日本、加拿大、美国、中国香港、巴西、法国和意大利的31名专家学者参与了这次会议,Briaud和Gibbens对收到的31份预测报告进行了分析和总结,这些报告总计采用了22种预测方法(包括有限元法),但没有人能对所有基础作出误差小于20%的预测,基础发生 25 mm沉降的荷载Q25平均被低估27%,说明砂土地基的沉降是难以准确预测的.
载荷试验能够模拟基础受荷之后地基的非线性变形性状,该试验通常被认为是最可靠的原位测试项目.我国已将基于载荷试验的沉降计算方法(变形模量法)列入地基规范[2].焦五一[3]最早提出依据载荷试验曲线分段确定地基土在不同应力水平下的弦线模量,用来预测地基的非线性沉降,该方法已经在黄土地基中得到很好的应用;杨光华[4]提出对载荷试验曲线进行双曲线拟合,采用双曲线切线模量计算地基的沉降.李仁平[5-6]提出依据载荷试验曲线对切线模量进行修正,然后采用修正切线模量分析地基的沉降问题.考虑到土体的多样性,实际工程中许多地基的载荷试验曲线并不能总是很好地采用双曲线进行拟合,因此本文提出一种更为通用的非线性沉降预测方法——修正弦线模量法,并采用上述基础加载试验成果进行验证.
1 修正弦线模量法
1.1 基本原理
根据压板试验曲线的起始直线段可以确定出土体的变形模量,其方程为

式中,ω为刚性承压板的形状系数,圆形承压板取0.79;方形承压板取0.88;d为承压板的直径或边长; μ为土的泊松比.
假定地基土某一压缩层的附加应力大小在pzi-1~pzi之间,取载荷试验曲线上pi-1=pzi-1,pi=pzi,相应的变形参数弦线模量为
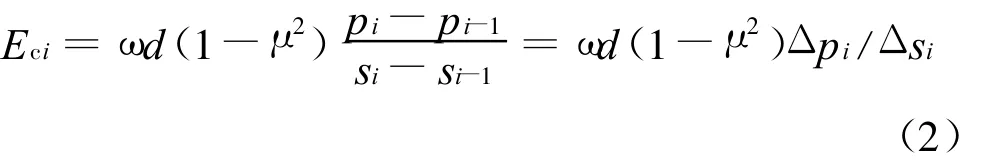
上述公式将计算的压力段延伸到沉降曲线的非线性变形阶段.根据载荷试验曲线计算得到的变形参数表征的是压板下整个地基土体的变形习性,由于土体埋深的影响,与承压板底面相接触的土层与其下有一定埋深的分层土在相同附加应力段产生的地基沉降是不同的,埋深越大,土层受到周围土体的围压越大,相应土层压缩量就越小,因此根据载荷试验沉降曲线确定的弦线模量必定是偏小的,亦即直接采用弦线模量计算地基沉降会导致计算结果偏大.为了修正这种偏差,引入一种精确算法——反馈修正法,以计算曲线与试验曲线分段相吻合为条件,确定出不同附加应力水平段的修正弦线模量,相应的计算公式为

式中,E′ci表示的是地基土层在附加应力段pzi-1~pz1 (对应于载荷试验曲线pi-1~pi压力段)的修正弦线模量值.若地基深度z处计算得到的地基附加应力为pz,相应的修正弦线模量为E′ci,在z处上下各取分层土厚度Δ h的一半,则该分层土在附加应力作用下产生的压缩变形Δs为:相应的分层压缩量为

假设地基压缩层共分n层,各分层厚度取Δ h,当压板荷载由0逐级施加到pn时,压板下地基总的沉降量为
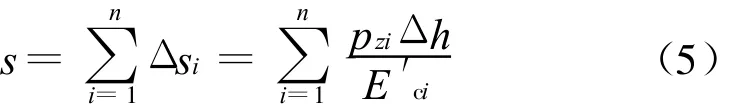
式中,βi是待定系数(即弦线模量修正系数),依据第i级荷载的压板计算沉降与试验值相等为条件反求得到.由于分层压缩量Δh随着E′ci的增加而单调减小,因此任意附加应力段pzi-1~pzi的修正待定系数βi都是唯一的,并且它的值小于1.0.
对于多层地基,需采用载荷试验或深部载荷试验(如螺旋板载荷试验)确定基础附加应力影响范围内各个土层的修正弦线模量,然后计算地基的总沉降.
1.2 计算步骤及程序实现
地基附加应力的计算采用弹性半空间问题的Boussinesq解.应用Matlab 7.1实现了上述算法的计算机编程,计算步骤为:
(1)输入各土层载荷试验各级荷载下的实测数据(pi,si),在数据较少时,则应用3次样条插值法对数据进行插值拟合;
(2)计算各级荷载下地基中的附加应力分布;
(3)确定地基压缩层厚度及分层厚度,一般认为地基的压缩层厚度在2B~3B之间,本程序取4B,土体分层厚度取0.2m;
(4)选择修正系数βi收敛步长为0.001(从1.0开始递减),应用地基沉降公式(3)~(5)自动迭代求解各级荷载下的地基沉降,直至每一级荷载下地基的计算沉降与载荷试验沉降值二者差值绝对值小于后者的1/200,输出各个附加应力水平段的βi及E′ci;
(5)利用E′ci计算其它基础下的地基沉降并绘计算成果图.
2 修正弦线模量法的国际试验验证
本文以Briaud和Gibbens(1993)所做的1 m×1 m小基础的加载试验成果代替载荷试验成果,用来确定砂土地基不同应力水平阶段的修正弦线模量,然后采用该参数预测其它尺寸基础的非线性沉降曲线,并与试验曲线及其它方法的预测结果进行比较分析.
试验场地位于美国Texas A&M大学校园内,土层为均质中等密实含泥细砂,粒径为0.05~0.5mm,基础底面下5 m深度范围内的平均粒径D50=0.2 mm,SPT每0.3m的平均标贯击数为18击,CPT锥尖阻力为6 MPa,旁压试验测得的极限荷载为800 kPa,PMT模量为8.5MPa,DMT模量为30 MPa,土体内摩擦角为32°,土体容重为15.5 kN/m3,地下水位埋深4.9m,各种原位测试点位置及基础位置分布如图1所示.
表1是基础在建造之后的实际尺寸,每级基础加载荷载为极限荷载预估值的1/10,持续30 min.图2表示1m基础的加载试验曲线和计算曲线,根据原文提供的数据和试验曲线图,加载试验在荷载400、850、1200和1740 kN对应的基础沉降(加载时间取30min)分别为4、25、65.5和150mm,曲线中的各级荷载(100、200、300、…、1800kN)及相应的沉降值是依据三次样条插值的方法获得.通过比较发现,采用修正弦线模量法得到的荷载沉降曲线与原文中的试验曲线完全吻合,而直接采用公式(2)的弦线模量法的计算结果明显偏大.说明对弦线模量值进行修正是非常必要的,计算时砂土泊松比取0.25.
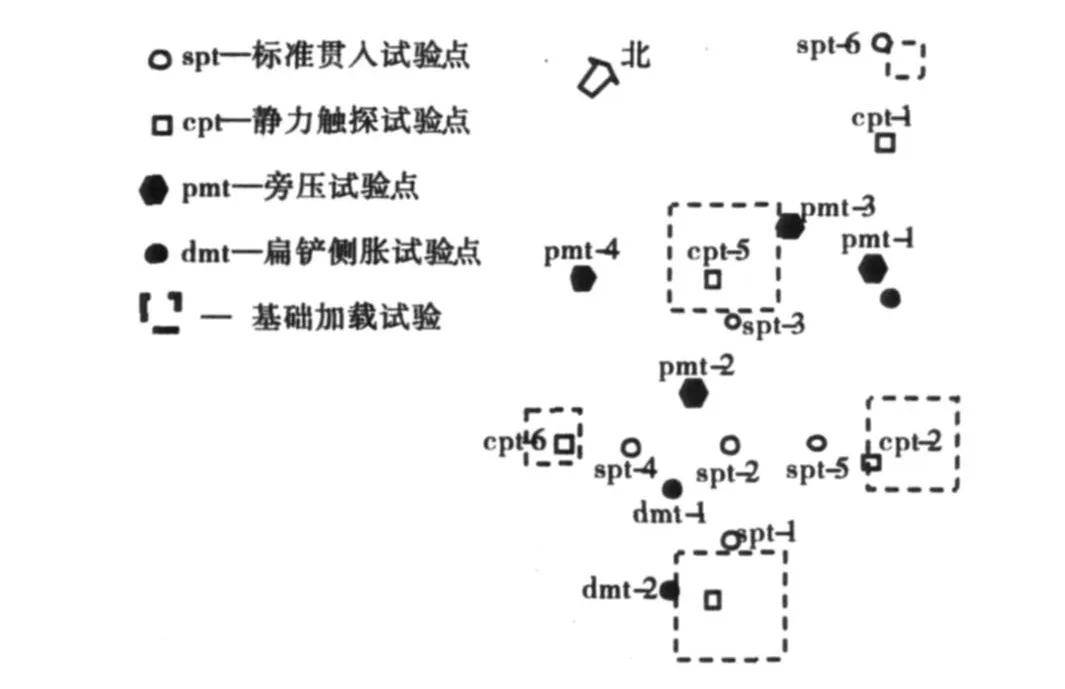
图1 现场试验平面布置图
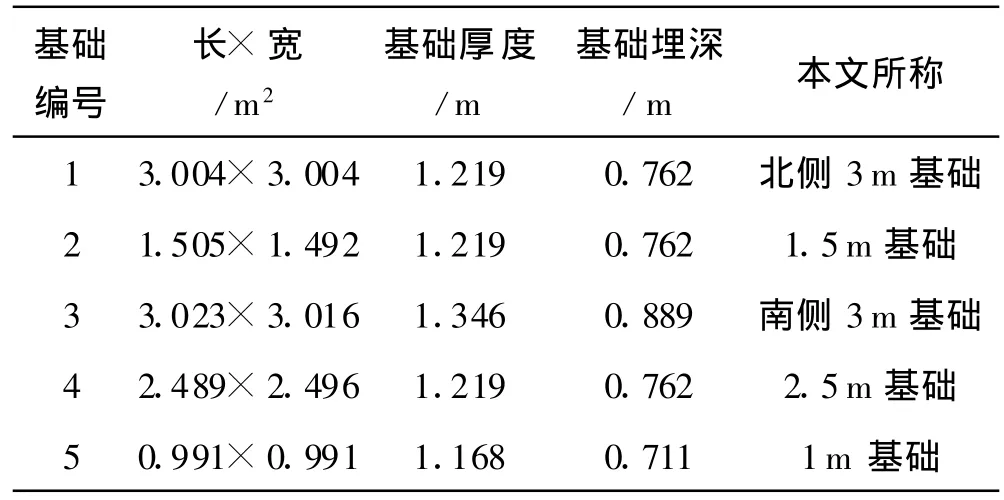
表1 建造后的基础尺寸数据
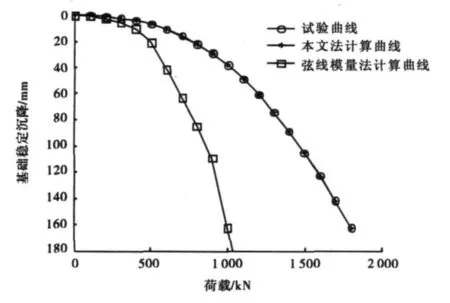
图2 1m基础加载试验曲线与沉降计算曲线
计算得到的各级荷载下的修正系数及各个附加应力段土体的修正弦线模量如表2所示.从表2可以看出,场地土体修正弦线模量随着附加应力水平的增加而减小,不同附加应力水平的模量值相差较大,修正系数βi介于0.2~0.6之间.
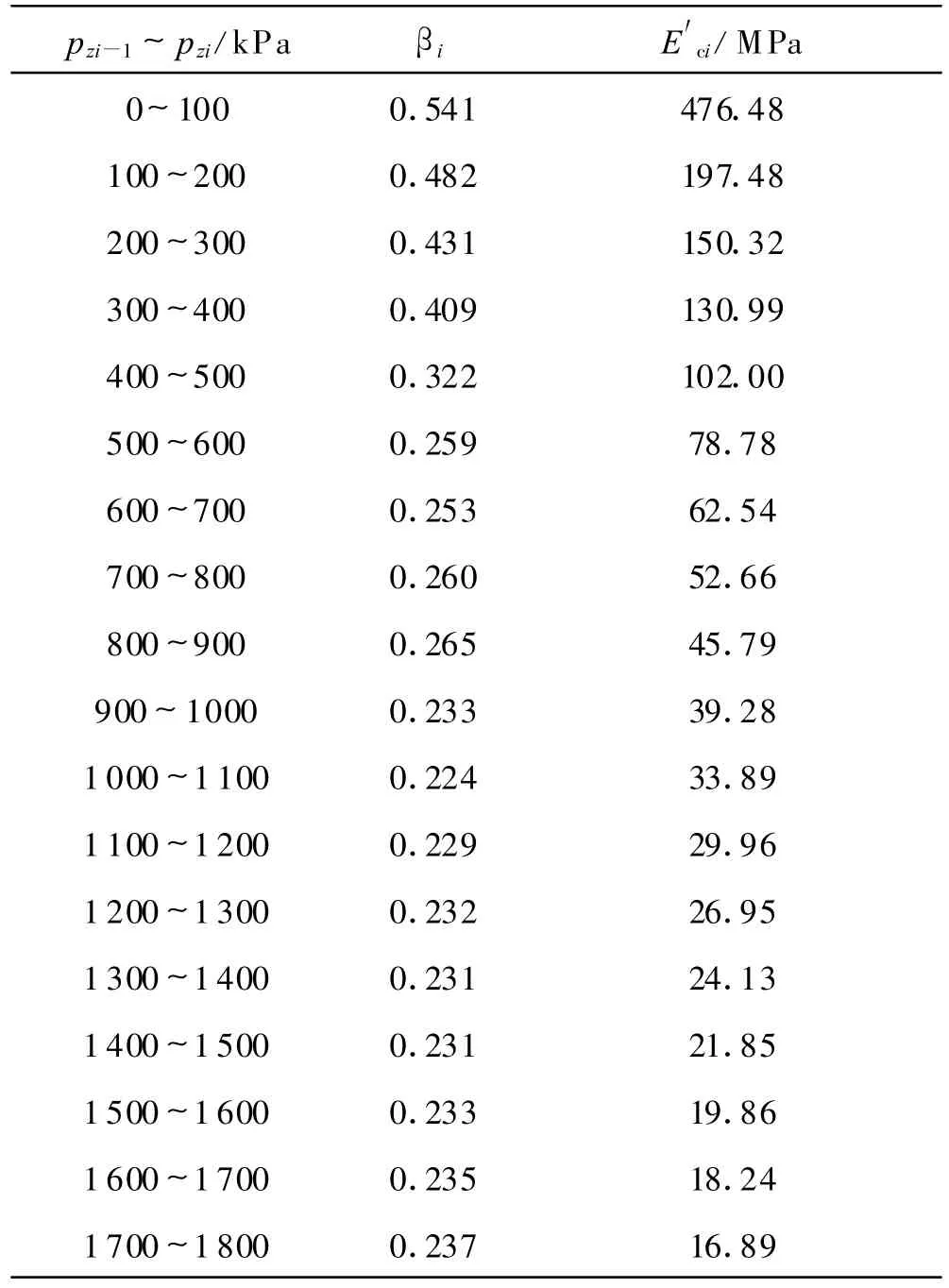
表2 不同应力水平条件下的修正弦线模量E′ci及βi
采用表2中的修正弦线模量值计算得到其它各个基础的荷载沉降曲线.图3~5分别表示1.5m、2.5 m和2个3m基础的加载试验曲线和计算曲线,可以看出,计算曲线均与试验曲线很好地吻合.
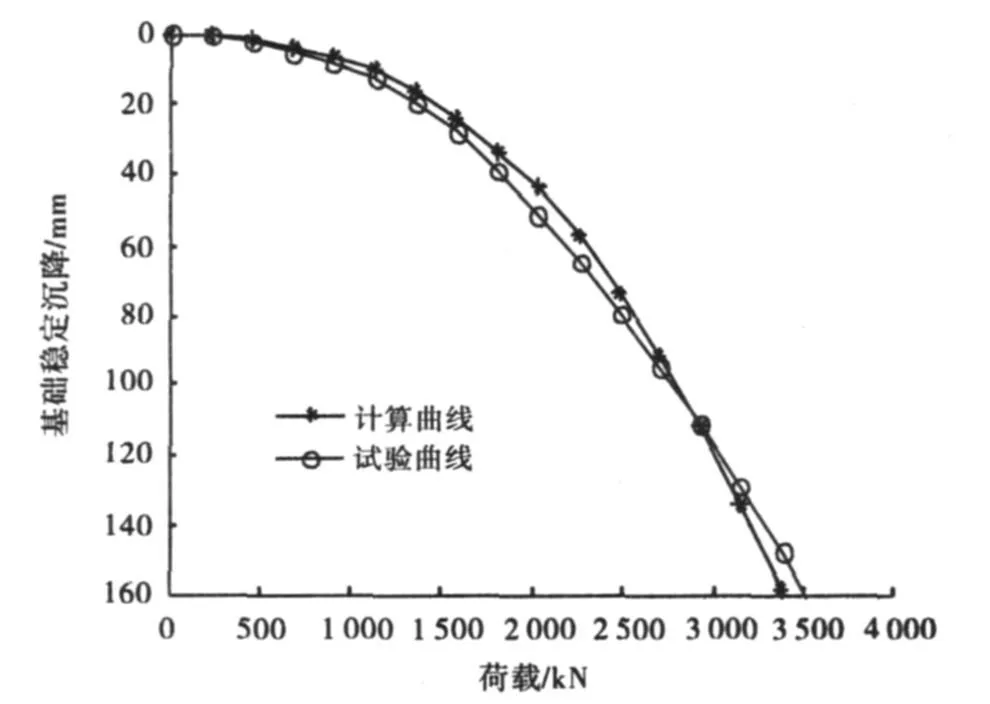
图3 1.5m基础加载试验曲线与沉降计算曲线
图5中北侧与南侧3 m基础的试验曲线不相吻合,是由于二个基础下的土层并非完全均质(有差异),而计算沉降曲线正好处在二者之间.
表3中的数据是各个基础分别在沉降25和150 mm对应荷载的试验值和计算值,可以发现,二者相差均在10%以内,说明采用修正弦线模量法得到的预测结果是相当可靠的.表4列出了这次国际研讨会31名学者的预测结果,可以看出,同一学者采用同一方法预测不同尺寸基础得到的沉降结果,往往预测精度相差较大,说明这些方法都无法反映基础沉降的尺寸效应.
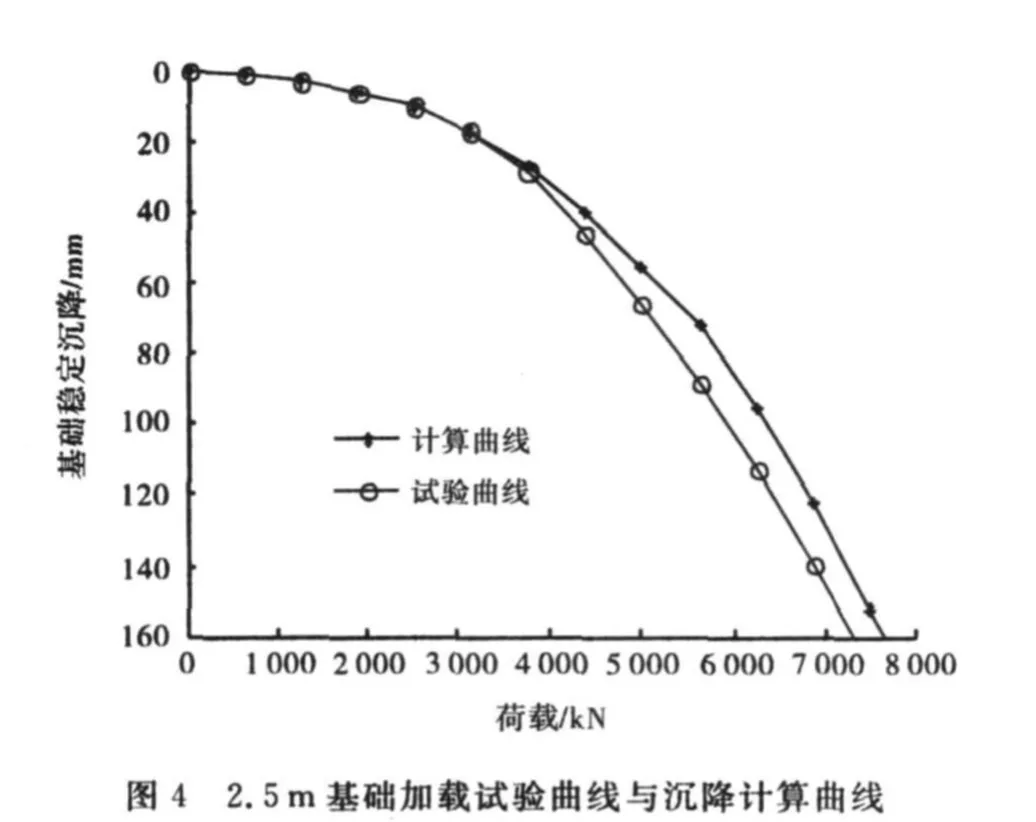
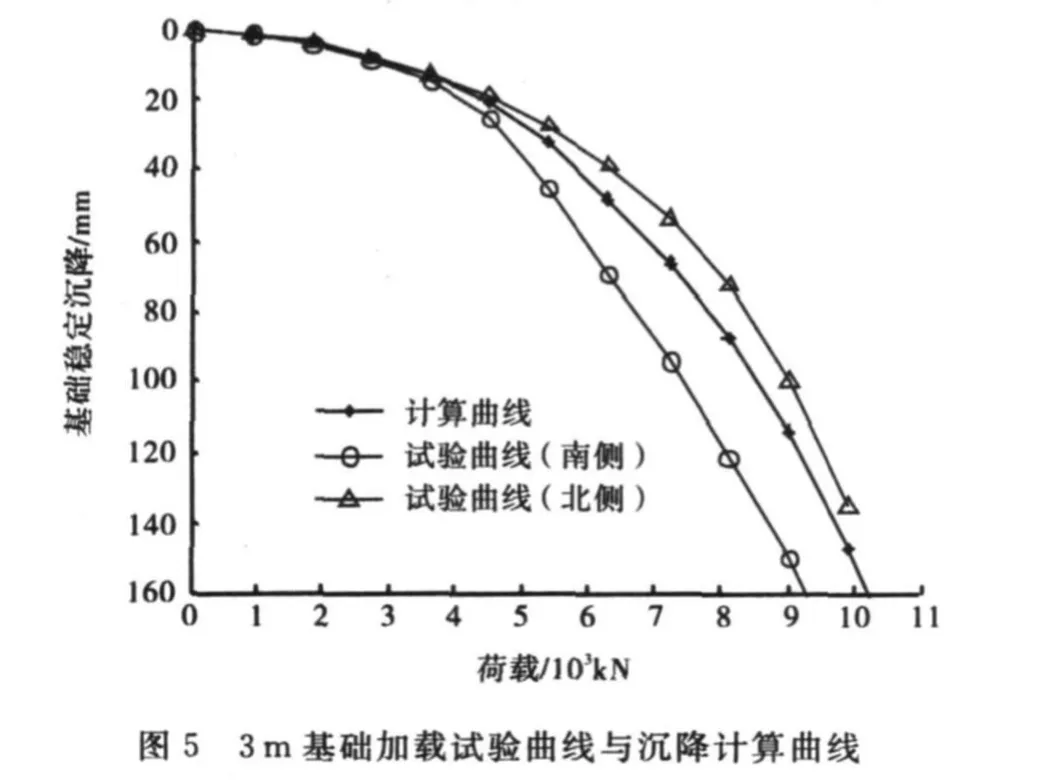
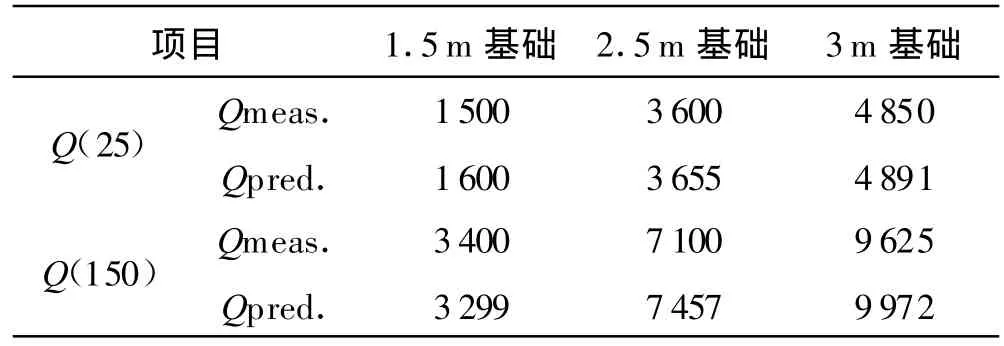
表3 各基础沉降对应荷载的试验值和计算值(单位:kN)

表4 Q25和Q150的沉降预测结果

续表4 Q25和Q150的沉降预测结果
表3、4中,Qmeas表示基础受荷30 min产生沉降25或150mm对应的荷载测试值,Qpred表示预测值.
3 结 论
(1)修正弦线模量是依据载荷试验曲线,以各级荷载下地基的沉降变形均与试验曲线相吻合为条件反求获得的变形参数,是一种非线性的等效变形模量,其值随附加应力水平的增加而减小,反映了土体的非线性变形特性.
(2)与弦线模量相比,修正弦线模量具有依据载荷试验曲线进行自动修正的功能(如土体泊松比取值不准确也不会影响修正弦线模量的大小),能够真实反映土体埋深等因素导致土体模量增加的情况,因此更加准确地反映了土体的变形特性.
(3)采用小尺寸基础(相当于载荷试验中的承压板)加载试验获得的修正弦线模量能够准确预测均质地基中较大尺寸基础的沉降,说明修正弦线模量法能够准确地反映基础沉降的尺寸效应.
(4)与31位学者采用的22种沉降预测方法获得的结果相比较,本文方法获得的结果更准确,与试验值相比,其误差在10%以内,验证了方法的可靠性.
(5)采用修正弦线模量法可以计算基础加载至极限状态的全过程曲线,预测精度能够很好地满足以变形控制为目的的基础工程设计要求.
本文的算例是砂土地基,本文方法可以推广到砂土等无粘性土地基;对于粘性土地基,地基沉降达到稳定的持续时间很长,如何利用修正弦线模量法预测粘性土地基的沉降量,是下一步的研究内容.
[1] Jean-Louis Briaud,Robert Gibbens,Predicted and Measured Behavior of Five Spread Footings on Sand:Results of a Spread Footing Prediction Symposium[M].American Society of Civil Engineers,Geotechnical Special Publication,No.41,1994.
[2] JGJ72-2004.高层建筑岩土工程勘察规程[S].北京:中国建筑工业出版社,2004.
[3] 焦五一.地基变形的新参数--弦线模量的原理和应用[J].水文地质与工程地质,1982(1):30-33.
[4] 杨光华.地基非线性沉降计算的原状土切线模量法[J].岩土工程学报,2006,28(11):1927-1931.
[5] 李仁平.用双曲线切线模量方程计算地基非线性沉降[J].岩土力学,2007,29(7):1987-1992.
[6] 李仁平.基于原位试验成果的地基非线性沉降分析[J].岩土力学,2009,30(2):345-351.
