一种基于Rank变换的改进中值滤波
2011-03-07夏道平董方敏潘天浩
夏道平 董方敏 潘天浩 姚 刚 刘 勇
(1.三峡大学智能视觉与图像信息研究所,湖北宜昌 443002;2.三峡大学科技学院,湖北宜昌 443002; 3.三峡大学电气与新能源学院,湖北宜昌 443002)
图像滤波技术可以从复杂的图像信号中提取所需要的信号,抑制不必要的信号,使图像更加清晰.近年来主要有两大类滤波方法:一类是空域滤波器,如均值滤波[1-2],中值滤波[3-5],统计滤波[6]等,由于此类方法的滤波效果主要取决于对像素邻域的处理方法和邻域大小,而对邻域处理的同时会模糊了图像细节,从而丢失了图像信息;另一类频域滤波,如高斯滤波[1],巴特沃斯滤波器[1],基于小波变换[7]的滤波算法等,由于此类滤波方法主要是对图像高频分量进行处理来实现图像滤波,而图像边缘和噪声频率分量均在高频部分,所以对高频分量进行降噪的同时,会使得边缘被错误判断为噪声点,从而使得图像目标信息被滤除,丢失了图像信息.近年来,由Matheron G和Serra J等人创立的形态学滤波器[8]是从数学形态学中发展出来的新型的非线性滤波器,利用预先定义的结构元素对信号进行匹配和局部修正,达到抑制噪声的目的.目前发展出组合形态学滤波[9]、自适应形态学滤波[10]、多结构元素滤波[11]等改进的形态学滤波方法,但是这些滤波方法主要存在的问题是在抑制噪声的同时模糊了图像,丢失了图像信息.
Tukey在1971年提出的中值滤波[12-13]是一种常用的非线性滤波方法,标准的中值滤波存在最大缺点是由于它对图像中所有像素点采用统一的处理方法,这种处理改变了噪声点的值,也有可能改变信号点的值,并有可能产生新的噪声等问题.本文针对目前中值滤波方法中存在丢失图像细节的问题和误判噪声点问题,对中值滤波算法进行了改进,引入Rank变换,对孤立噪声点和连续噪声点进行滤波处理,期望能达到既可有效保持图像细节,又能实现较好的图像滤波效果.
1 Rank变换及其噪声检测原理
像素的Rank变换是以该像素点为中心取一个矩形区域(称为Rank窗口),统计Rank窗口中所有灰度值小于中心像素灰度值的像素的个数,并以这个数代替原来中心像素点的灰度值.通过每个像素的Rank变换后,整个图像被转换为一个整数矩阵,这个整数矩阵称为Rank图像[14].
定义1 设f(x,y)表示图像当前像素(x,y)的灰度值,N(x,y)表示以(x,y)为中心的矩形窗口像素集合,则对像素(x,y)的Rank变换定义为

如图1所示3×3窗口的中心像素f(x,y)的灰度为160,由(1)、(2)式,N(x,y)转换为δ(x,y),求δ (x,y)所有元素的和,即为 f(x,y)以 N(x,y)为Rank变换窗口的Rank变换值r(x,y).也可以直接从N(x,y)中看出,有5个像素灰度值小于中心像素,因此r(x,y)=5.图1显示了求解的过程.经过Rank变换后,像素的灰度值(0~255)就转换为一个范围较小的整数(0到R-1,R是N(x,y)内的像素总数).
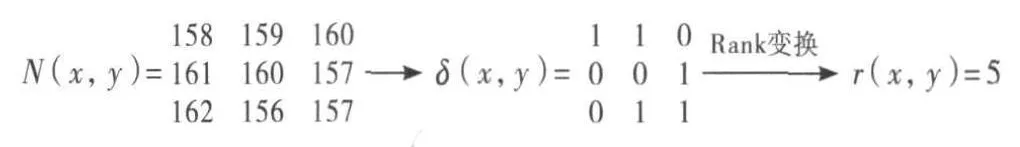
图1 Rank变换求解过程
孤立点即满足中心像素点f(x,y)与窗口(窗口大小3×3)邻域点f(x+ξ,y+η)之间的如下关系:
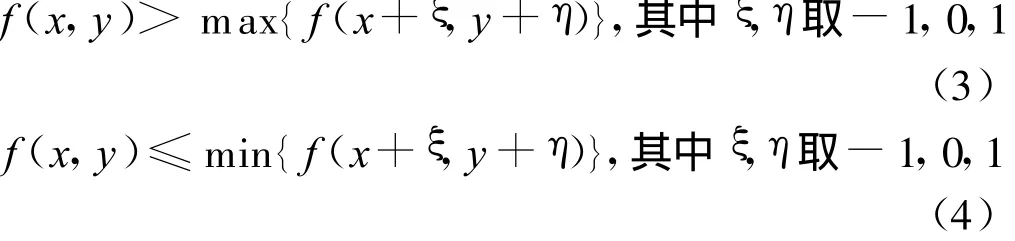
如果将原始图像经过Rank变换后,在Rank变换域内孤立点(x,y)应该满足式(5),其含义表示在滤波窗口内中心像素值要么均大于相邻像素值,要么均小于相邻像素值,这样可以认为中心像素点是孤立点.
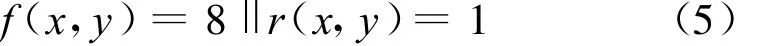
2 基于Rank变换的改进中值滤波算法
本文所提出的基于 Rank变换的中值滤波算法主要分以下2个步骤.
Step1:利用Rank变换检测出孤立点.对于图像像素点,边缘点一般都是连续的,孤立点一般都是噪声,也有可能是边缘点,利用这个特性,可以将图像中所有的孤立点单独检测出来进行滤波;本文正是利用Rank变换的特性,将图像灰度值转换为中心像素点f(x,y)和其邻域之间的相关特性,对图像 f(x,y)使用公式(1)和(2)进行Rank变换得到r(x,y),最后利用孤立点特征式(5)检测出图像上的孤立点.
Step2:遍历整个图像像素点,对孤立点进行中值滤波,取孤立点的领域窗口,并对窗口内像素进行排序取中值,用中值代替孤立点的值;对非孤立点仍然保留原灰度值不变.遍历整个图像的像素点.
通过以上算法的步骤及分析可知,本文提出的基于Rank变换的改进中值滤波算法相对传统的中值滤波算法的优势在于:传统中值滤波算法是针对图像所有像素点无论是噪声点还是非噪声点都进行中值替换处理,这样会导致丢失图像细节;而本文提出的基于Rank变换的改进中值滤波算法主要分成两个阶段:第一个阶段主要是分辨噪声点和非噪声点;第二个阶段则专门以噪声点为对象进行中值滤波处理,而对于非噪声点将保留原灰度值,因此,很好地保留了图像细节,从而避免模糊图像.
3 基于Rank变换的中值滤波迭代算法
对于一幅图片而言,可能既存在离散的噪声点,也有可能存在连续的噪声点,而本文上述算法只适合于离散的噪声点的处理,而对于连续的噪声点不能进行有效的滤波.针对上述算法的弊端,可以进一步提出迭代改进算法如下.
Step1:利用Rank变换检测出孤立点;
Step2:遍历图像所有像素点,对孤立点进行中值滤波,非孤立点仍然保留灰度值不变;
Step3:对 step2结果进行多次迭代操作,重复step1,step2;
Step4:如果第i次迭代和第i+1次迭代图像上的每个限速的Rank变化结果没有变化,即整个图像r(i,j)值趋于稳定,停止算法.
本文分别提出了两种基于 Rank变换的改进中值滤波算法,其算法的核心思想是通过检测图像上的噪声点,然后对噪声点进行滤波,而对非噪声点不做任何处理,首先从算法复杂度上,本文算法仅仅对图像上部分被检测出的噪声点进行处理,而原始中值滤波算法则需要对图像上每个像素都进行处理,所以算法的复杂度比原中值滤波算法要低;而对于时间复杂度,本文算法和原中值滤波算法的复杂度均取决于图像的大小,算法的时间复杂度是相同的.
4 实验结果及分析
实验过程采用256×256的Lena图片作为实验对象.对图像添加0.05的椒盐噪声进行实验.如图2所示是将本文提出的算法及改进算法和传统几种滤波算法进行的对比实验结果.

图2 椒盐噪声图像对比
从图2可以看出,对于椒盐噪声,均值滤波由于是对图像中每个像素都进行领域处理,因此滤波效果不是很理想(如图2(c));中值滤波对图像中每个像素使用中值进行平滑,收到比较好的效果(如图2 (d));而本文提出的基于Rank变换的中值滤波效果比较理想,不用对全部像素点都用中值进行平滑,只需要对检测出来的噪声点采用中值平滑,不仅能很好地消除大部分噪声,还能很好地保持图像细节信息,没有模糊图像(如图2(e)),而改进的迭代算法在上述两者上有更明显的优势,得到了非常好的滤波效果(如图2(f)).
为了验证算法的通用性,图3将本文算法及改进算法和几种传统滤波算法进行了对比实验.从图3可以看出,均值滤波由于是对图像中每个像素都进行领域处理,因此滤波效果不是很理想,如图3(c)所示;中值滤波对每个像素点进行中值平滑,效果一般,如图3(d)所示;本文提出的改进中值滤波效果对于高斯噪声而言,没有椒盐噪声滤除效果理想,但相对传统滤波算法而言,仍然有较好效果,改进的迭代算法的滤波效果如图3(f)所示.

图3 高斯噪声图像对比
从两组对比试验中看到,本文所提出的算法对于椒盐噪声更有效,而对于高斯噪声,由于噪声的分布比较连续,所以所检测出来的噪声点也是连续的,所以进行中值操作的像素点会比较多,也会造成图像部分像素点产生模糊现象.噪声的产生是一个随机过程,噪声分布的概率密度函数很难使用数学函数来表达,通常使用信噪比来衡量噪声强度.为了说明本文提出算法的可行性和通用性,本文在对比滤波算法滤波效果的同时采用峰值信噪比PSNR[1]来衡量.计算结果见表1.
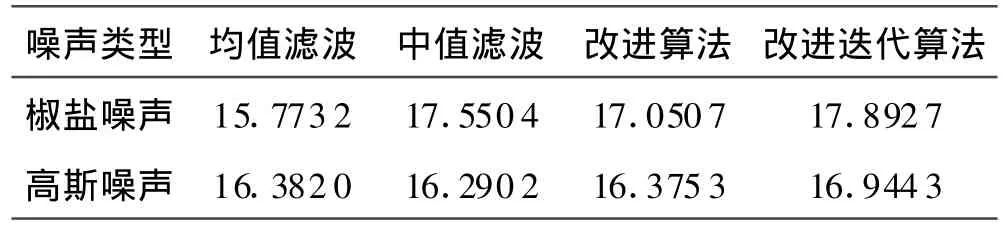
表1 PSNR滤波评价参数
从表1中可以看出,本文提出的两种算法的峰值信噪比是最大的,说明本文算法相对于原始图像的失真度最小.由图2,图3的视觉效果和表1的数据,说明本文算法具有很好的滤波效果.
5 结 论
本文提出了一种基于Rank变换的改进中值滤波算法,对于目前滤波过程中所存在改变图像细节,产生新的噪声,模糊细节等问题进行了改进和优化,能较大程度解决上述问题,并达到较好的图像滤波效果.本文提出的算法仍然无法解决噪声点个数远大于像素总数一半,即噪声密度较大时,滤波效果较差的问题;本文在检测噪声点的过程中,没有考虑像素之间的位置关系,同时通过迭代算法来解决连续噪声问题导致了算法效率不高等问题,有待在后续研究中进一步改进.
[1] Gonzalez R C,Woods R E.数字图像处理[M].2版.阮秋琦,阮宇智,译.北京:电子工业出版社,2003:132-148.
[2] 蔡 靖,杨晋生,丁润涛.模糊加权均值滤波器[J].中国图象图形学报,2000,5(1):52-56.
[3] Hwang H,Haddad R A.Adaptive Median Filters:New Algorithmsand Results[J].IEEE Trans.Signal Process,1995,4(4):499-502.
[4] 王晓凯,李 锋.改进的自适应中值滤波[J].计算机工程与应用,2010,46(30):175-176.
[5] 张 恒,雷志辉,丁晓华.一种改进的中值滤波算法[J].中国图形图像学报,2004,9(4):408-411.
[6] Arce G.Detail-preserving Ranked-order Based Filter for Image Processing[J].IEEE Trans.Acoust,Speech, Signal Processing,1989,37:83-98.
[7] 焦李成,谭 山.图像的多尺度几何分析:回顾和展望[J].电子学报,2003,13(12):1975-1980.
[8] Serra J.Morphological Filtering:An Overview[J]. IEEE Trans.Signal Processing,1994,38(1):3-11.
[9] 陈 虎,周朝辉,王守尊.基于数学形态学的图像去噪方法研究[J].工程图学学报,2004,2(2):116-119.
[10]赵春晖,乔景渌,孙坚和.一类多结构元自适应广义形态滤波器[J].中国图像图形学报,1997,11(2):806-809.
[11]杨平先,孙兴波,干树川.一种改进的数学形态学图像滤波算法[J].华北电力大学学报,2005,33(6):56-59.
[12]黄 颖,王卫星.分类中值滤波算法的研究[J].计算机工程与应用,2009,45(11):34-36.
[13]Wang Xiaokai,Li Feng.Improved Adaptive Median Filtering[J].Computer Engineeringand Applications, 2010,46(3):175-176.
[14]郭龙源,夏永泉,杨静宇.RANK变换在立体匹配中的应用研究[J].系统仿真学报,2007,19(9):2121-2123, 2126.
