门式起重机防摆控制系统模型
2011-03-07何孔德方子帆杨蔚华
何孔德 方子帆 杨蔚华
(三峡大学机械与材料学院,湖北宜昌 443002)
门式起重机被大量应用于制造业、港口运输业及大型精密装备的装配中,其吊运空间有限、吊重大、吊装位置要求精确,稍有不慎,就会造成货物解体或损害其自身结构[1].而且随着悬吊钢丝绳长度的增大,门式起重机的负载在快速定位上要花费较长时间,影响了生产效率,因此有必要研究如何快速稳定吊重,并设计其控制系统,有效提高工作效率和安全性.本文通过建立门式起重机动力学模型及其状态空间方程,利用LQR线性二次最优控制方法对其摆动进行了分析,采用Matlab对其进行仿真.结果表明,这种控制方法能有效降低门式起重机的摆动时间,提高定位精度和工作效率,对作业安全性具有重要意义[2].
1 门式起重机力学模型
门式起重机是靠两个水平往复运动的综合来完成重物吊运的,将吊重水平方向运动的运行机构和吊重上下运动的起升机构组合起来,就能使门式起重机为一个长方形面积及其上空的空间服务.为了便于分析影响门式起重机吊重摆动的本质,根据工作中的实际情况对其作简化处理:门式起重机在作业过程中,大车一般处于静止状态,因此不考虑大车的运动;小车在行走的过程中忽略起升钢丝绳的长度变化;吊重始终处于水平状态且只在垂直于水平的平面内运动,这样吊具和吊重可以简化为无体积的质点;忽略风力和空气阻力,不计系统的弹性变形;忽略电机、减速器等传动机构的非线性影响;假设小车与轨道之间的摩擦力和小车速度成线性关系[3];忽略钢丝绳与小车连接处的摩擦力,通过以上的假设可得到简化后的力学模型,如图1所示.

图1 小车-吊重系统力学模型
本文以MG型门式起重机为例进行研究,其参数及图1中各符号所表示的意义见表1[4].

表1 模型参数及符号意义
2 门式起重机系统动力学方程
2.1 系统运动微分方程
依据图1,系统受到的力有小车和吊重的自身重力,小车的驱动力,小车与轨道的阻力.由于假设L不变,则此系统具有两个自由度,取图1中X,Y所示的方向为正向,以小车A的坐标 x和缆绳的摆角θ为广义坐标,建立广义坐标下的系统运动学方程.
小车和吊重的速度分别表示如下:

系统的动能:
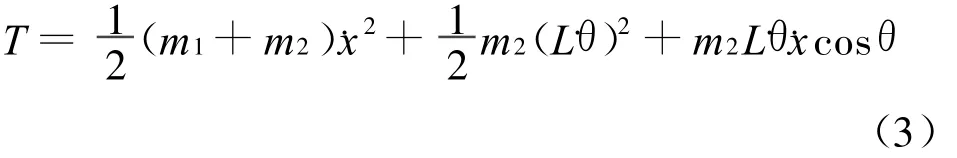
可得其运动微分方程为

2.2 系统的传递函数与状态方程
由于门式起重机吊重过程中钢丝绳的长度比吊重摆动幅度要大得多,所以θ很小,线性化处理,sinθ =θ,cosθ=1,则其运动微分方程可写为

对式(6)、(7)进行拉氏变换得:

系统的传递函数为

依据式(6)、(7),取θ,˙θ,x,˙x为系统的状态变量, x,θ为系统输出,F为系统的输入,则系统状态方程为
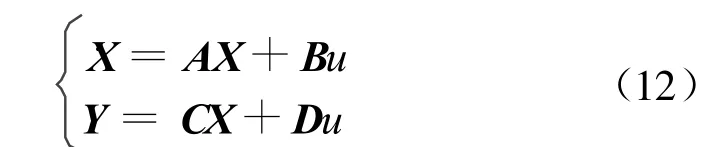
其中,X=[θ,˙θ,x,˙x],u=F,Y=[θ,x]T,则将式(6), (7)改写为矩阵形式:

即

2.3 模型参数确定
依据表1,带入具体参数,得系统的传递函数为

系统的状态方程为

3 LQR线性二次型最优控制原理
文中控制系统设计的目标是使起重机在最短时间内定位于指定位置,即此时载荷无摆动.由于性能指标均为控制变量的二次型函数积分,故该系统可以视作二次型性能指标的最优控制问题[5].线性二次型最优问题的最优解可以以统一的解析形式表示,可求得状态线性反馈控制规律,由此而构成一个闭环最优反馈系统.其状态方程性能指标为

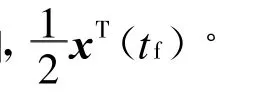

其实现最优控制的必要条件为
(1)状态方程:

(2)协态方程:

(3)边界条件:

(4)横截条件:

(5)极值条件:

由式(25)得输入为

即为使性能指标达到最小的最优控制输入函数.其中,λ(t)可由式λ(t)=P(t)x(t)求出.因此

由于R、B均为已知,所以求最优控制u*(t)的问题就等效于求解矩阵P,由庞特李雅金极大值原理知,存在矩阵P满足静态黎卡提方程为
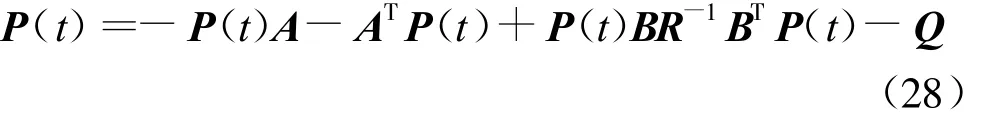
解方程求得P,从而得到最优控制规律:
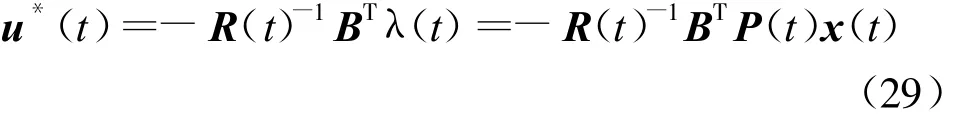
4 LQR控制系统设计与仿真
4.1 系统在未进行LQR控制之前的仿真
利用Matlab软件进行仿真分析,求解起重机吊重在未进行LQR控制之前摆角的仿真曲线,如图2所示.
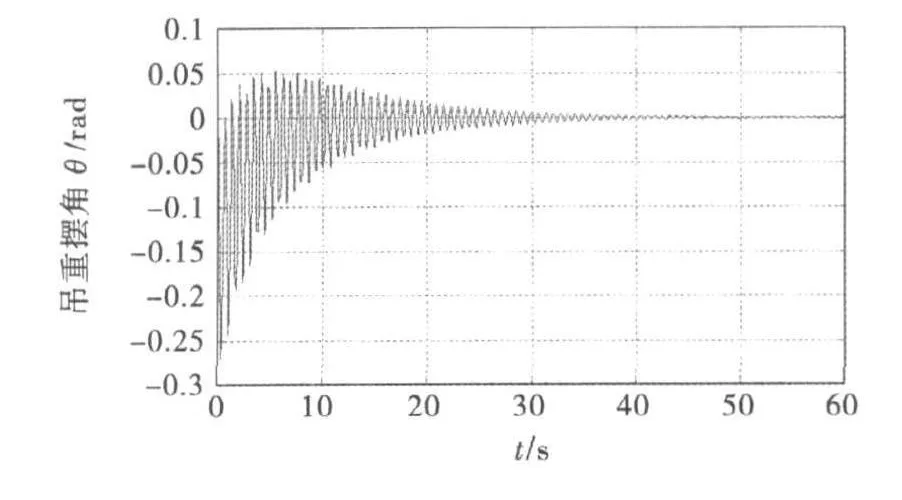
图2 未控制前吊重摆角响应曲线
从图2可以看出小车在到达指定位置的过程中,由于小车与轨道间存在阻尼,吊重摆动角度随着时间的推移而衰减,但是衰减速度较慢且衰减过程中其振荡频率高,不利于起重机的实际操作.
4.2 LQR控制系统分析与设计


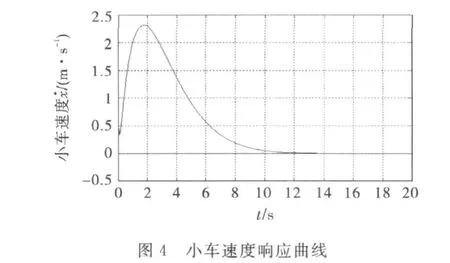
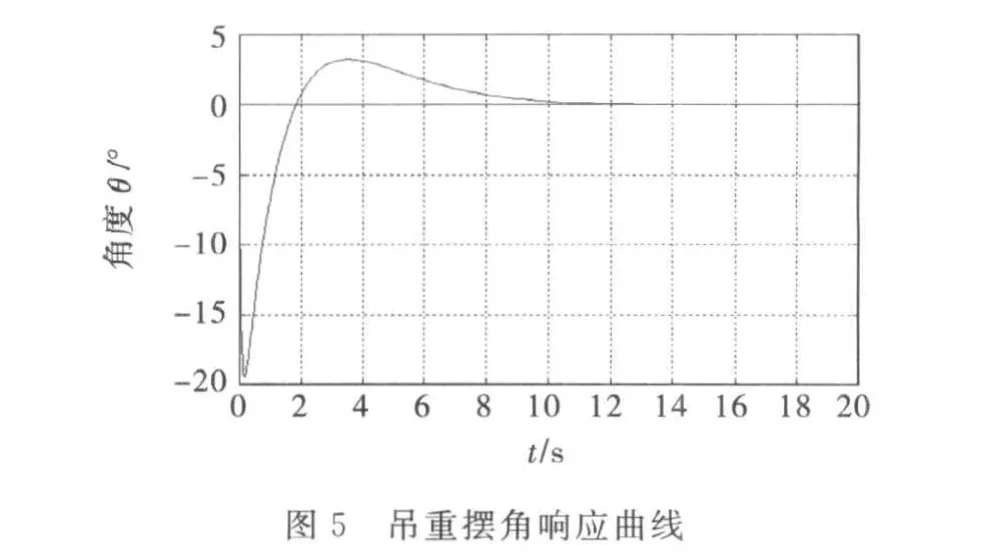

从图3~4可以看出,门式起重机运行小车的位移达到预设位置10m处花费的时间是11s,此时小车速度趋于稳定.从图5~6可以看出,吊重摆角达到稳定位置花费的时间是12s,此时摆角接近于0,角速度趋于稳定,说明该控制器能够使控制方程的状态变量在很短的时间内达到期望值,即实现小车在到达预定位置的同时消除负载的摆动.
5 结 论
本文应用拉格朗日方程建立了门式起重机系统的数学模型,并推导出其运动微分方程及状态空间方程,对采用控制器前和采用LQR最优控制方法后起重机防摆问题进行了仿真研究,并在Matlab环境下进行了仿真.可以看出,LQR控制器能够使状态方程的状态变量在要求时间内达到零,即在运行小车达到既定位置时快速消除吊重的摆动,使吊重精确定位.在此基础上可以进一步进行控制器硬件的设计,设计出控制系统.这种方法也可以推广运用到其它起重机的防摆控制系统设计上.
[1] Khalid L.Sorensen,William Singhose,Stephen Dickerson.A ControllerEnablingPrecise Positioningand Sway Reduction in Bridge and Gantry Cranes[J].Control Engineering Practice,2007(15):825-837.
[2] 陈 翔.国际集装箱运输发展趋势及经营对策[J].中国水运,2008(11):18-19.
[3] 白传悦.岸边集装箱起重机吊具减摆装置[J].起重运输机械,2005(8):23-44.
[4] 李 伟,李瑞华.起重机智能控制的发展现状与思考[J].煤矿机械,2006,27(8):3-4.
[5] 王晓军,邵惠鹤.基于模糊的桥式起重机的定位和防摆控制研究[J].系统仿真学报,2005,26(4):936-939.
[6] 李 茂,曾昭龙,李文秀.舰载起重机的智能控制系统仿真研究[J].系统仿真学报,2004,16(4):791-793.
[7] 梁承姬,张纪元.机械式减摆机构的动力学模型及其数值计算[J].上海海运学报,2005,21(4):37-42.
