海上风电MPPT灰预测模糊控制的研究
2011-03-07卢佳奇熊和金
卢佳奇 熊和金
(武汉理工大学自动化学院,武汉 430063)
与陆上风力发电相比,海上风电场除在解决占地和环保方面具有明显优势外,还有明显的技术优越性.无论国内还是国外,海上风力发电已经成为一个新能源开发的重点[1-3].
风力发电的整个过程实际上就是风能由机械能转换成电能的物理过程,转换的整个过程主要由风力发电系统完成,它包括风力机和发电机两部件,其中风力发电机及其控制系统是整个系统的核心.其中永磁同步发电机无需齿轮箱、机械损耗小、运行效率高、维护成本低而成为风力发电的发展方向[4-5].
目前国内风电机组大多采用的是PID控制器完成最大功率的跟踪.但由于速度变化的随机性和风电机组的强非线性,PID控制算法不能取得令人满意的效果.不管是经典PID控制、模糊PID控制还是灰色预测模糊PID控制,它们都是反馈控制方法,只有当机组实际功率与设定功率出现偏差时,控制器才开始调节[6-7].
1 系统控制原理
图1是本文研究的风力发电MPPT模糊控制系统的拓扑结构,该系统包含以下内容:变速风力机、永磁发电机、三相不控整流桥、Sepic变换器,电压源逆变器和升压变压器.

图1 风电MPPT模糊控制系统的拓扑结构
就永磁发电机而言,当轴上输入的机械功率大于发电机的输出电功率时,发电机的转速就会增加;当轴上输入的机械功率小于发电机输出的电功率时,转速将要下降.在图1所示的系统中,永磁发电机输出端线电压只有在大于三相不控整流桥输出端电容的电压时,发电机才有功率输出.而发电机的输出端电压是由转速决定的.发电机的转速越高,输出的电压就越大.因此,不控整流桥输出端电容上电压的大小就决定了发电机输出功率时的转速大小,即电容上的电压越大,相应的发电机发电时的转速就越高.因此,通过改变三相不控整流桥输出端电容电压的大小,就可以控制发电机运行时的转速,实现风力机的变速运行以达到MPPT控制目的.
2 永磁同步电机的数学模型
为建立永磁同步发电机的理想模型,可对其进行如下的理想化处理:假设气隙中磁通按正弦分布;电压和电流的高次谐波可以忽略;铁芯损耗可以忽略.此时可以在d-q轴同步旋转坐标下建立数学模型:
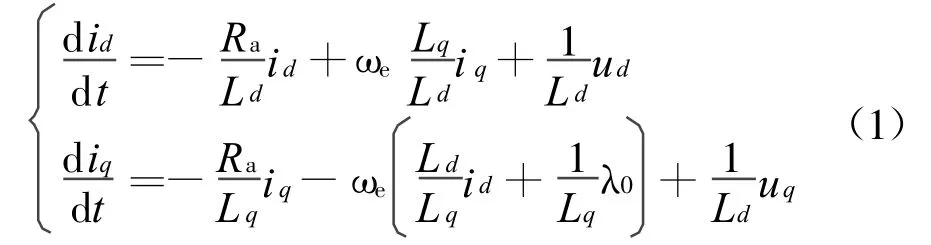
式中,id和iq分别为永磁同步电机d轴和q轴的电流:Ld和Lq分别为永磁电机d轴和q轴的电感;ud和uq分别为永磁同步电机输出电压d轴和q轴的分量;Ra为定子电阻;λ0为永磁体的磁通系数;ωe= npωg为电角频率,np为转子极对数;ωg为转子转速.
假设Ld=Lq=L,则式(1)可简化为
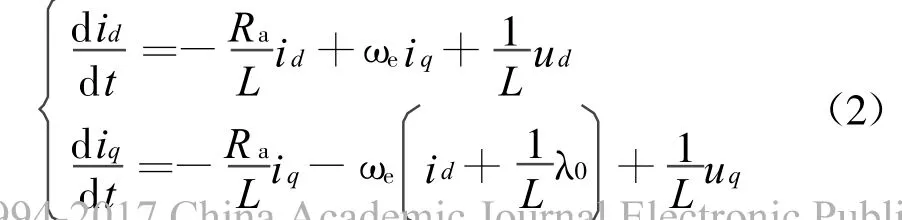
永磁同步电机的输出电磁转矩为

机械方程式为
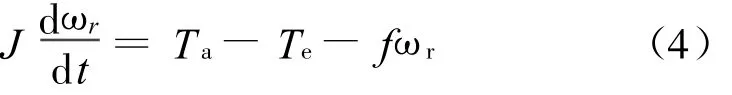
式中,J为转动惯量;f为摩擦系数.
3 控制系统设计
3.1 传统PID控制分析
风电机组并网运行后,如果风速发生变化,永磁发电机轴上输出机械功率发生变化导致电机转速改变,系统输出功率不能保证最大跟踪.通过占空比控制,改变三相不控整流桥输出端电容电压的大小,维持风电机组在最大功率下运行.虽然PID控制器在较大风速变化范围内能够完成控制任务,但效果并不十分理想,原因如下:
(1)风电机组在额定风速以下运行时,其特性呈现很强的非线性.占空比控制对应的输出电压变化对风力机最大输出功率的影响在不同风速下差别很大,一组整定好的PID参数在固定风速附近控制效果比较理想,但当风速增加或减小时,控制效果变得很差.
(2)PID控制器属于反馈控制器,只有当偏差出现时,控制才会起作用.其特性存在一定的惯性和延迟,因此不可避免地造成较大的超调和较长的调节时间,使机组输出功率波动过大,给电网造成较大的冲击.
本文针对上述缺点,提出灰色预测和模糊PID控制结合的新型控制方法,控制系统结构图如图2所示.
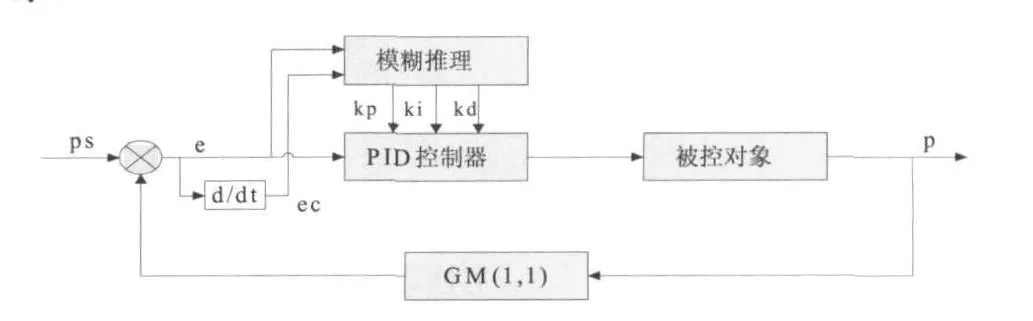
图2 灰色预测和模糊PID控制结合的控制系统结构图
其中:ps为单一风力机在给定风速下的理想输出功率,p为发电机实际输出功率,GM(1,1)为灰预测模型.
3.2 模糊PID控制器设计
模糊控制鲁棒性好,抗干扰能力强,对复杂对象或难以建立精确数学模型的对象具有很好的控制效果.但模糊控制器自身消除系统稳态误差的性能较差,难以达到较高的控制精度,在控制点附近会出现盲区和死区.模糊PID控制器是模糊控制与PID控制器的结合,在较大偏差范围内利用模糊推理的方法给出控制量,达到快速稳定的调节;而在小偏差范围内切换为PID控制,从而实现稳态误差的消除.两者的转换根据事先给定的偏差阈值自动实现.模糊PID控制器可以较好地克服上文指出的PID控制器的缺点.当模糊控制器规则建立后,只需一组PID参数即可达到较好的控制效果.仿真表明,由于模糊PID控制器中的PID控制器主要作用是消除稳态误差,其参数整定应适当小.
模糊控制器的输入有两个:功率误差和误差的变化率.本文所讨论的风电机组的额定功率为300 kW,用于PID参数调整的模糊控制器采用二输入三输出的模糊控制器,该控制器以误差e和误差的变化率ec为语言变量,而以kp、ki和kd为输出语言变量.各变量的模糊论域为{-6,-5,-4,-3,-2,-1,0,1,2, 3,4,5,6},模糊子集为{NB,NM,NS,ZO,PS,PM, PB}.为保证功率信号跟踪的快速性及其稳定性,隶属函数采用三角形隶属函数,确定功率跟踪模糊控制规则见表1(其中依次为kp、ki和kd的控制规则).
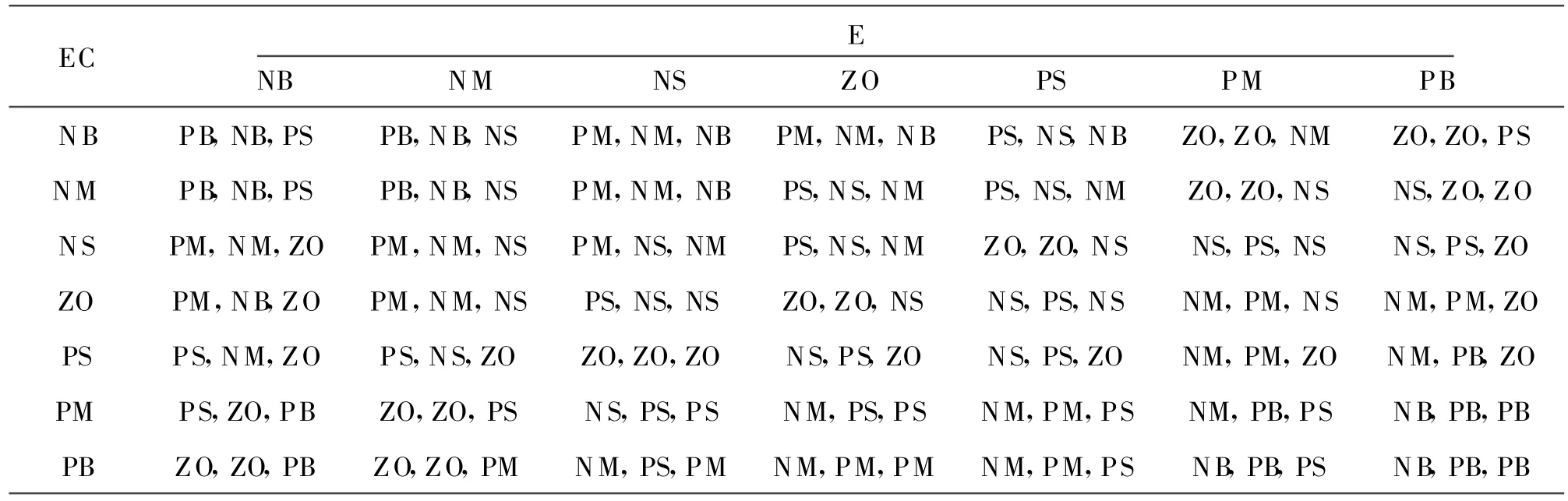
表1 模糊控制规则表
3.3 灰预测模糊控制
灰色系统是指既含有已知信息,又含有未知和非确定信息的系统,也称为贫信息系统.在灰色系统理论中,称抽象系统的逆过程为灰色模型,亦称GM.典型的灰色系统为GM(1,1)模型.设该模型原始序列为

这是一组信息不完全的灰色量,具有很大的随机性,将其进行生成处理,以提供更多的有用信息.选用累加生成,则m次累加生成的结果为
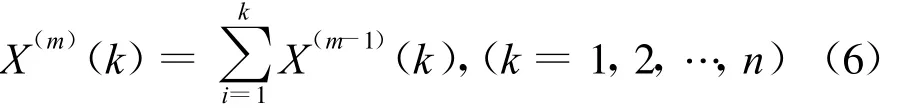
在累加生成时,一般用一次累加就能使数据呈现一定的规律,若规律不够,可以增加累加生成的次数.
在数据生成的基础上,用线性动态模型对数据拟合和逼近,其形式为
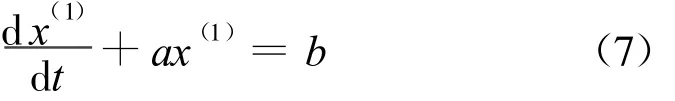
微分方程的解为
微分方程的系数可用最小二乘法求出,其向量形式为
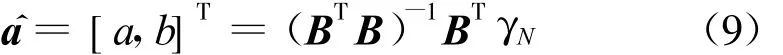
式中:
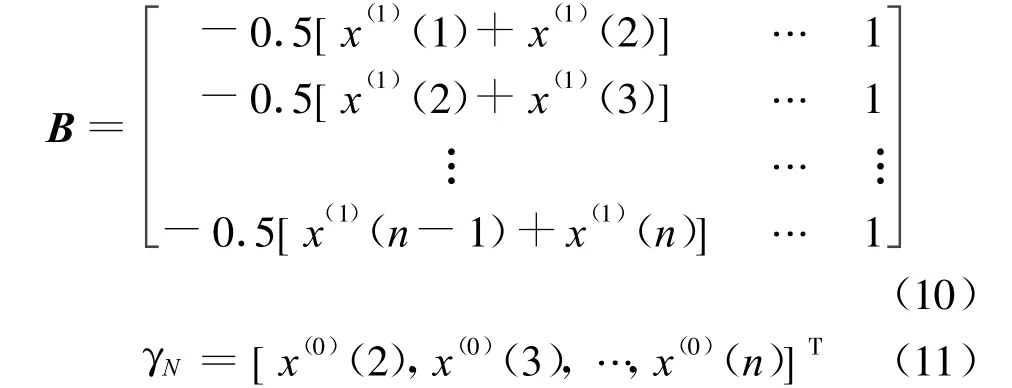
按照
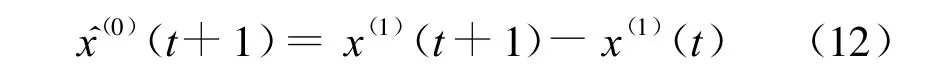
累加生成还原,即
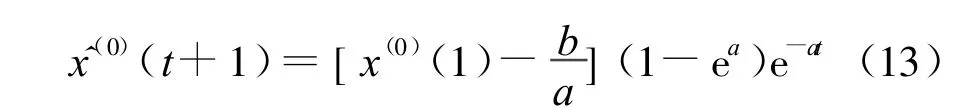
通过计算以后得到数据.
因为灰色模型预测为局部的曲线拟合推论策略,对于一阶单一变数的灰色预测模型而言,至少需要4组数据方能提供相当正确的灰色预测.在本文研究中,针对风速的随机变化,选取前5个时刻的风速数据x(k-4),x(k-3),x(k-2),x(k-1)与x(k),使用灰色模型以累加预测下一步的输入风速^x(k+1),运用于模糊控制策略中,计算下一步的功率误差及误差变化率.
4 仿真试验结果
采用Matlab软件中的Simulink的SimPower-System提供的风力机模型,参数设定为:Nominal mechanical output power(W):30631;Base of electrical generator(VA):27567.6;Base wind speed (m/s):12;Maximum power at base wind speed(pu of nominal mechanical power):0.73;Base rotational speed(p.u.of base generator speed):1.2;Pitch angle:0.
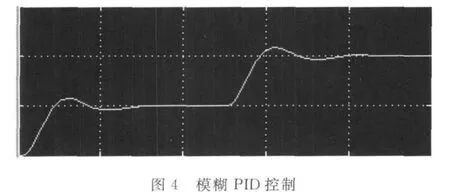
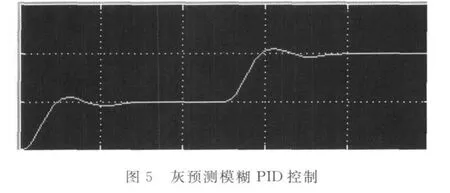
在5s时,风速由8m/s到12m/s变化,3种控制策略的功率输出如图3~5所示.

给定变化后的各控制策略的参数如表2所示.
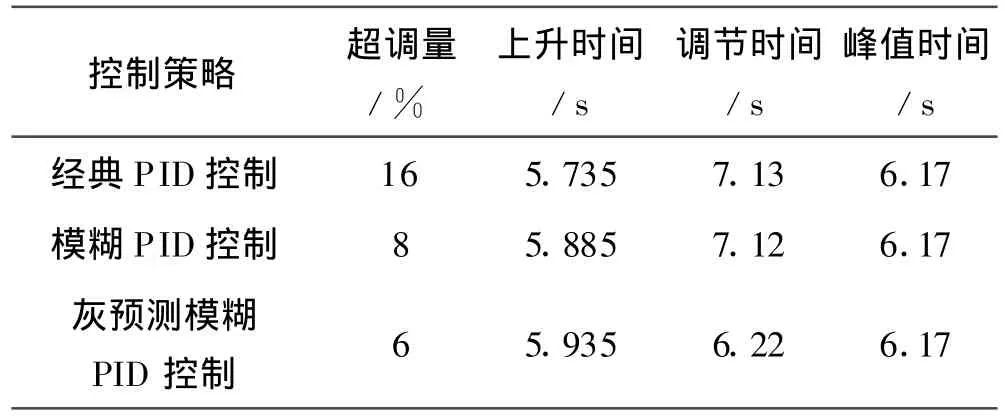
表2 参数对比表
仿真结果可以看出灰预测模糊PID控制效果比传统PID和模糊PID要好,在牺牲了一点快速性的基础上,稍微延缓了上升时间,但是在调节时间和超调上都优于前两者,具有更好的稳定性.
5 结 论
由于风电机组的强非线性,传统的PID控制在海上风力发电中难以达到满意的控制效果,本文将模糊控制引入到海上风电中,并在此基础上,将灰色预测和模糊控制相结合.模糊PID控制器能够解决传统PID控制参数整定困难的问题,而灰色预测则能够在模糊控制整定参数中给予适当的补偿,实现快速跟踪功率的目的.仿真效果表明,本文的控制策略取得了比较满意的效果.
[1] 高 坤,李春凳.新型海上风力发电及其关键技术研究[J].能量研究与信息,2010,26(2):110-116.
[2] 赵 群,柴福莉.海上风力发电现状与发展趋势[J].机电工程,2009,26(12):5-8.
[3] 李晓燕,余 志.海上风力发电进展[J].太阳能学报, 2004.2.
[4] 郭 鹏.模糊前馈与模糊PID结合的锋利发电机组变桨距控制[J].中国机电工程学报.2010,30(8):123-128.
[5] 徐大平,吕跃刚.大型风力发电机组的自适应模糊控制[J].太阳能学报,2004,16(3):573-577.
[6] 熊和金,徐华中.灰色控制[M].北京:国防工业出版社, 2005.
[7] 苗 瑜.基于灰色模型的预测模糊温度控制系统[J].控制工程,2008(S1):134-135.
