机械结构可靠性计算方法

李四超，张代国，张强

（海军驻郑州地区军事代表室，河南郑州 450015）

0 引言

根据我国目前的实际情况，机械产品的可靠性工作必须从定性的设计、分析入手，发现薄弱环节，从而改进设计，使定性分析起到影响设计、提高可靠性的作用;与此同时，还要通过积极的研究来逐步积累数据，以实现机械产品的定量设计和评估，从而验证可靠性是否达到了规定的指标要求。本文研究重点是机械产品的结构可靠性的定量分析方法。在研究过程中，首先对机械结构（以下简称结构）可靠性一般的定量分析方法进行了深入探讨，在此基础上，提出一种结构可靠性计算的改进方法，可求解出一般结构在确定置信度下的可靠性置信区间。

1 机械结构可靠性计算的一般方法

1.1 结构可靠性计算的基本假设［1］

为了进行有效的结构可靠性计算，做出如下基本假设;

1）结构强度为一非负的随机变量或随机过程，用R或R（t）表示;

2）应力为一非负的随机变量或随机过程，用S或S（t）表示;

3）当应力不超过结构强度时，结构被认为是可靠的，否则被认为是结构失效;

4）结构失效仅由于应力作用而发生;

5）计算应力和强度的一切力学公式仍然适用，但公式中的确定量均视为相互独立的随机变量或随机过程。

1.2 应力－强度干涉模型的建立

结构可靠性计算的理论基础是应力－强度干涉模型。在该模型中，应力和强度均是概率意义上的量，设计时不能予以精确地确定，需要通过随机变量的有关综合运算确定应力和强度的均值μ和标准差σ。随机变量的计算目前主要有代数运算、泰勒级数近似求解和蒙特卡洛模拟3种方法。

通过采用合适的随机变量计算方法，可以得出应力和强度2个随机变量的分布。设应力S的概率密度函数为fs（S），强度T的概率密度函数为fR（T），则结构可靠度的表达式为［2］:

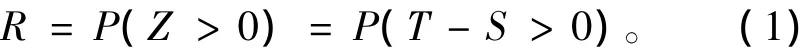
图1为应力S和强度T的概率密度函数曲线。图中2条曲线的重迭部分称为干涉区，它是结构可能出现失效的区域。干涉区的面积愈小，结构的可靠度就愈高;反之，可靠度就愈低。根据干涉区进行结构可靠性计算的理论称为应力－干涉理论，这种模型称为干涉模型。从干涉模型可以看出，欲确定结构的可靠度R，

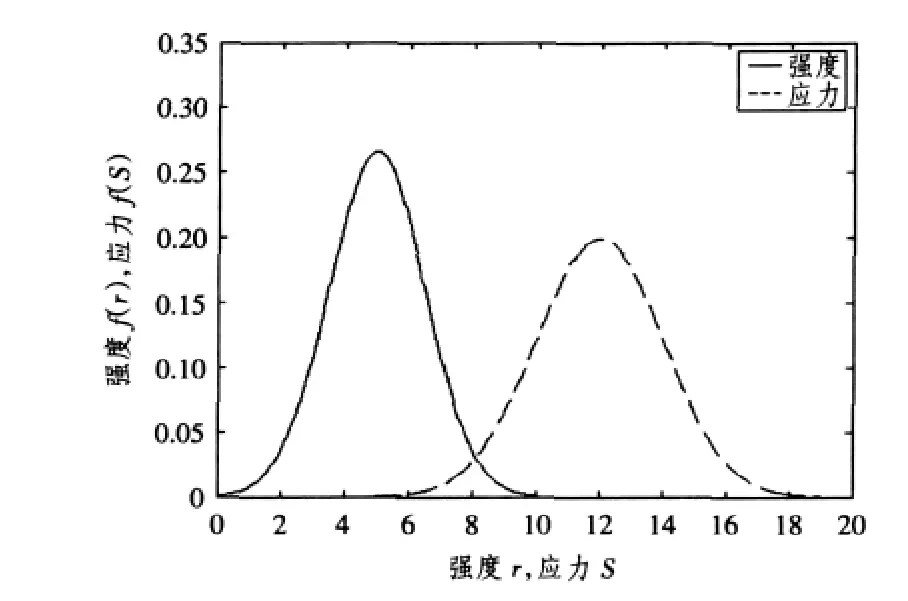
图1 强度－应力干涉示意图Fig.1Stress-strength interferogram

必须研究应力和强度2个随机变量中一个超过另一个的概率，即:

式（2）是在应力和强度相互独立的假设下得出的。一般情况下，应力和强度为独立随机变量的假设是正确的，这与工程实际相符。但有时就不能把应力和强度考虑为独立的随机变量，譬如需要考虑结构本身重量或由重量引起的自重应力时，就须考虑它们的相关问题。此时，设应力和强度的联合密度函数为fS，T（S，T），则可得结构可靠度普遍的表达式:

1.3 强度和应力的确定方法

1）材料强度的获取方法

在采用应力－强度干涉模型对结构可靠性进行分析时，关键是需要知道材料强度和结构承受应力的分布及特征参数，只有在得出应力和强度的分布参数后，才可根据式（3）对结构的可靠性进行分析计算。

经过长期研究，人们认识到材料的强度服从正态分布，并得出了部分材料拉伸强度极限和屈服极限的均值和标准差的数据，同时给出了材料变异系数的数值。大量统计表明:金属材料强度的变异系数一般小于0.10，最大不超过0.15，当变异系数小于0.3时，认为材料的强度取正态分布是可以接受的。

变异系数按下式定义［3］:

一般材料特性的变异系数可参考表1。

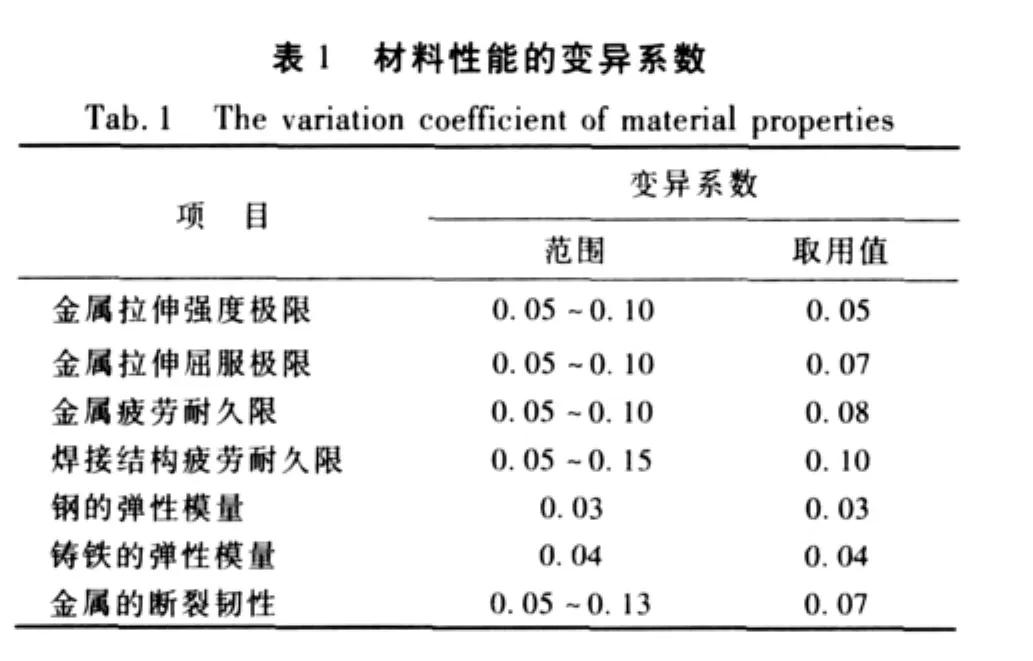
在一般机械设计手册中没有给出强度（或屈服）极限的均值和标准差，而只给出了材料强度的单一值，此时可认为该单一值即为材料强度的平均值μr。若变异系数Cr为0.10，则强度的标准差为:

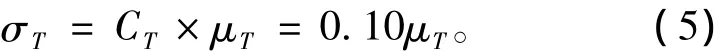
2）应力的确定方法

应力的均值可按传统的材料力学方法进行确定，即根据结构承受的载荷，尺寸等变量按一定的数学模型进行求解。采用该方法时，应力均值的求解较为简单，但应力标准差的确定却很复杂，此时可采用蒙特卡洛方法［4－5］进行计算。

在确定了强度和应力后，即可采用应力－强度干涉方法求出金属结构件的可靠性。

1.4 典型应力和强度分布的计算模型

在多数情况下强度和应力服从正态分布，下面给出应力和强度为正态分布下的可靠度计算公式:

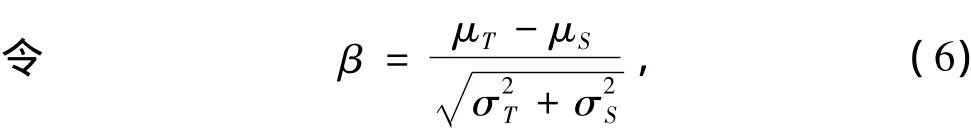
式中:μT和μS分别为强度和应力的均值;σT和σS分别为强度和应力的方差。

则可靠度为

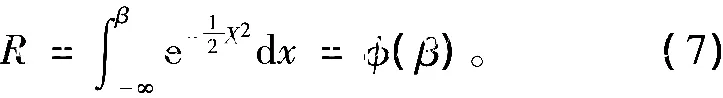
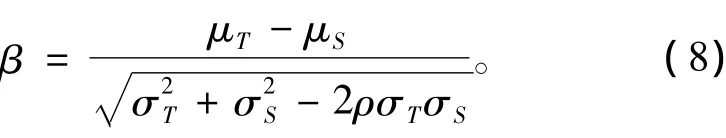
一般情况下，结构强度的均值μT大于施加在结构上的应力的均值μS，即μT－μS＞0。在这种情况下，可靠度均大于0.5，而可靠度具体数值还和σT及σS有关，σT和σS越大，则可靠度越小，反之可靠度越大。

当μT－μS=0，可靠度等于0.5，其数值与σT和σS无关;当μT－μS＜0，可靠度小于0.5。

对于可靠度小于及等于0.5的结构，在设计过程中应绝对避免。若应力和强度不是相互独立，则令:

2 应力－强度干涉模型的改进

2.1 传统计算方法存在的不足

上节给出了采用应力－强度干涉模型进行结构强度分析的一般方法，但该方法在实际运用中存在一定的局限性［6］。

1）在大多数工程问题中，结构强度和应力的分布参数是未知的，需要抽取一定数量的样本进行试验，通过统计的方法获取强度和应力的均值、方差等特性参数，然后再利用式（6）和式（7）对结构的可靠度进行计算，得到可靠度是在某一确定置信度下的一个置信区间;

2）在大多数场合下，应力是无法直接得到的，而是需要用一个非线性的表达式进行描述，此时可靠性因子β也相应地转换成一个非线性的表达式，而不能用式（6）直接求得。

针对以上2点不足，需要寻求一种改进的结构可靠性计算方法，使之能更加普遍地适应于一般结构的可靠度计算。

2.2 改进计算模型的建立

定义式（1）中的Z=T－S为结构可靠性分析的状态函数，即当Z＞0时，结构是可靠的。在一般情况下，状态函数Z是多个随机变量的函数，即Z= g（X1，X2，…，Xn），设X1，X2，…，Xn服从正态分布，但分布参数为未知的随机变量。

将Z展开成泰勒级数，忽略高次项，可得:

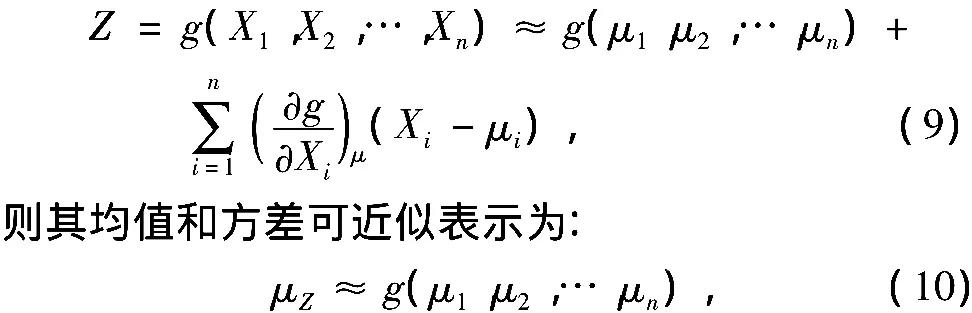
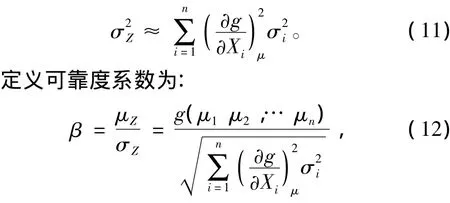
式中，μi和σi分别为Xi的均值和方差。可得可靠度系数β的点估计值为［7］:

将式（13）在各随机变量均值和方差的真值处展开成泰勒级数，仍仅取级数的线性项，忽略高次项，则有

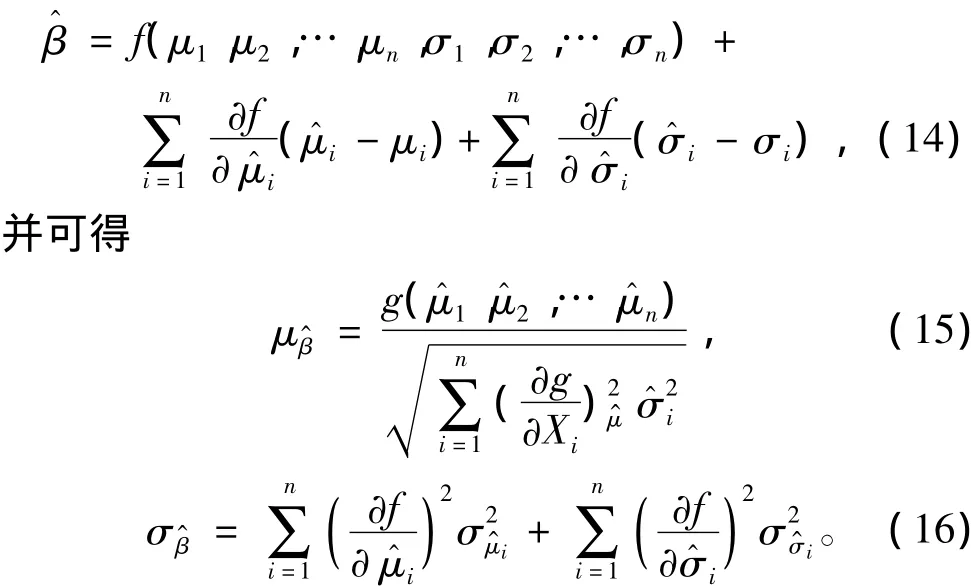
式中，各随机变量Xi的均值和方差需用样本估计值进行近似计算。

设β^服从正态分布，对于给定的置信水平H，可靠度系数β的双侧置信区间为:

3 结语

本文对传统的强度－应力干涉模型进行了探讨，研究了作为随机变量的应力和强度的确定方法，并针对传统的计算方法存在的不足，提出了一种改进计算模型，通过试验样本数据估计应力和强度在一定置信度下的取值，采用泰勒级数展开求解非线性极限状态的可靠性系数，采用改进的方法可求解结构在确定置信度下的可靠性置信区间。

［1］何水清，王善．结构可靠性分析与设计［M］．北京:国防工业出版社，1993．11－20．

［2］王善，何健．导弹结构可靠性［M］．哈尔滨:哈尔滨工程大学出版社，2002．10－12．

［3］都军民，蔡民，戴宗妙．基于可靠性安全系数的结构设计方法研究［J］．舰船科学技术，2007，29（3）:134－136．

［4］李良巧．机械可靠性设计与分析［M］．北京:国防工业出版社，1998．67－72．

［5］徐长航，陈国明，谢静．基于支持向量机和蒙特卡洛的结构可靠性分析方法及应用［J］．中国石油大学学报，2008，32（4）:103－107．

［6］都军民，李云翔．一种正态分布结构可靠性的改进算法［J］．河南科学，2009，27（5）:566－570．

［7］马逢时，何良材．应用概率统计［M］．北京:高等教育出版社，1989．35－42．